CompassArena 司南大模型测评--代码编写

news2025/1/15 6:24:00

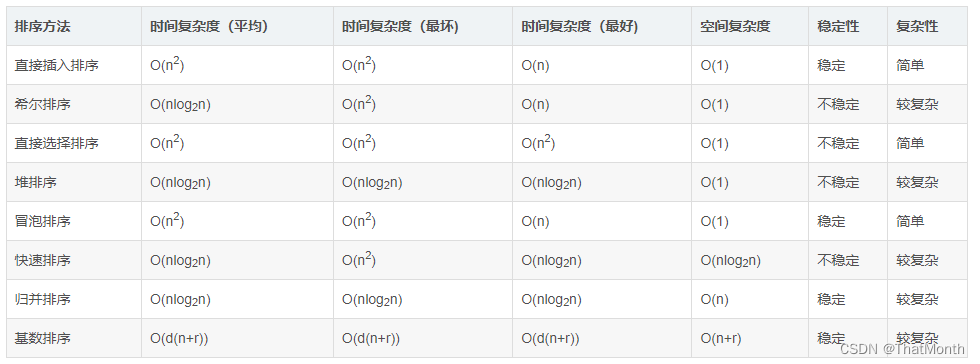
测试角度

要说测试模型，对咱们程序员来说，那自然是写代码的能力强不强比较重要了。那么下面我们以 leetcode 中的一道表面上是困难题的题目来考考各家大模型，看看哪个才应该是咱们日常写程序的帮手。

部分模型回答

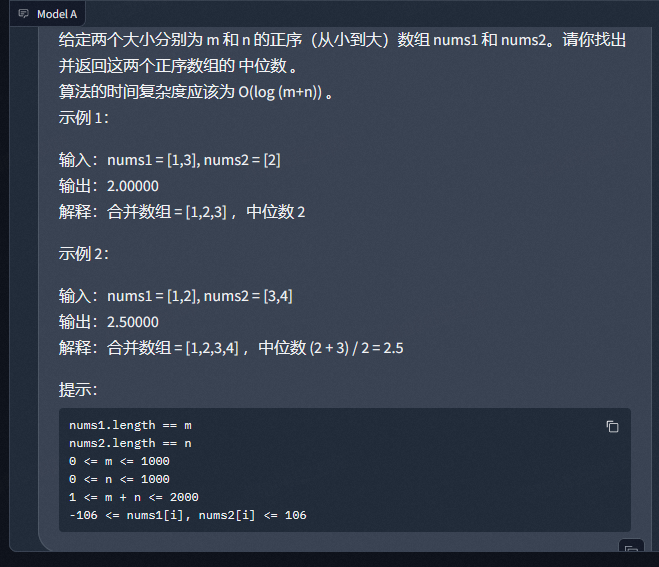
问题部分如下截图，后边就不再重复粘贴了，主要来看回答。我们注意到这里的难点在于在于对时间复杂度有要求，看看各个模型能不能注意到这一点。
出于篇幅，这里只贴出来结果比较好的几个模型进行点评。

图片.png

Abab6.5 Chat (MiniMax) 结果

要找到两个正序数组的中位数，并且要求算法的时间复杂度为 O(log (m+n))，可以使用二分查找的方法。以下是一种可能的解决方案：

  1. 首先，确保 nums1 是较短的数组，如果不是，则交换 nums1 和 nums2。
  2. 使用二分查找，在较短的数组 nums1 中查找合适的分割线，使得 nums1 分割线左侧的元素和 nums2 分割线右侧的元素个数之和等于 nums1 分割线右侧的元素和 nums2 分割线左侧的元素个数之和（或者相差1，如果总元素个数是奇数）。
  3. 通过比较 nums1 中分割线两侧的元素与 nums2 中分割线两侧的元素，调整分割线的位置，直到找到正确的分割线位置。
  4. 根据分割线的位置，计算中位数。

下面是具体的算法实现：

def findMedianSortedArrays(nums1, nums2):
    # 确保 nums1 是较短的数组
    if len(nums1) > len(nums2):
        nums1, nums2 = nums2, nums1
    
    m, n = len(nums1), len(nums2)
    total_left = (m + n + 1) // 2
    
    # 在 nums1 的区间 [0, m] 里查找恰当的分割线，
    # 使得 nums1[i-1] <= nums2[j] && nums2[j-1] <= nums1[i]
    left, right = 0, m
    while left < right:
        i = left + (right - left) // 2
        j = total_left - i
        if nums1[i] < nums2[j - 1]:
            # i 需要增大
            left = i + 1
        else:
            # i 需要减小
            right = i
    
    i = left
    j = total_left - i
    
    # 处理数组长度为奇数和偶数的情况
    nums1_left_max = float('-inf') if i == 0 else nums1[i - 1]
    nums2_left_max = float('-inf') if j == 0 else nums2[j - 1]
    nums1_right_min = float('inf') if i == m else nums1[i]
    nums2_right_min = float('inf') if j == n else nums2[j]
    
    if (m + n) % 2 == 1:
        return max(nums1_left_max, nums2_left_max)
    else:
        return (max(nums1_left_max, nums2_left_max) + min(nums1_right_min, nums2_right_min)) / 2

# 示例
nums1 = [1, 3]
nums2 = [2]
print(findMedianSortedArrays(nums1, nums2))  # 输出 2.0

nums1 = [1, 2]
nums2 = [3, 4]
print(findMedianSortedArrays(nums1, nums2))  # 输出 2.5

这个算法的时间复杂度是 O(log(min(m, n)))，因为二分查找是在较短的数组上进行的。

Abab6.5 Chat (MiniMax) 点评

Abab6.5 Chat (MiniMax)给出的答案是python写的，估计训练使用python的代码比较多。模型注意到了时间复杂度，并且一直在强调，且给出的代码是可运行的，算法描述也比较清晰，代码的质量中规中矩，且加了注释，还不错。

Baichuan 4 (百川智能) 回答

为了找到两个有序数组的中位数，我们可以使用二分查找的方法来减少时间复杂度到O(log(min(m, n)))。以下是解决这个问题的步骤：

  1. 确保nums1是较短的数组，如果nums1比nums2长，交换它们。这样做是为了优化二分查找的性能。

  2. 在nums1上执行二分查找，找到适当的分割线，使得nums1左边的元素和nums2左边的元素一起组成了整个合并数组左边的一半，同时nums1右边的元素和nums2右边的元素组成右边的一半。

  3. 调整分割线，以确保左右两边的元素数量相等或最多相差一个，这取决于合并后数组长度的奇偶性。

  4. 计算中位数。如果合并后数组的长度是奇数，则中位数是两个数组左边部分的最大值。如果是偶数，则中位数是两个数组左边部分的最大值和两个数组右边部分的最小值的平均值。

下面是这个算法的Python代码实现：

def findMedianSortedArrays(nums1, nums2):
    # 确保nums1是较短的数组
    if len(nums1) > len(nums2):
        nums1, nums2 = nums2, nums1
    
    m, n = len(nums1), len(nums2)
    imin, imax, half_len = 0, m, (m + n + 1) // 2
    while imin <= imax:
        i = (imin + imax) // 2
        j = half_len - i
        if i < m and nums2[j-1] > nums1[i]:
            # i太小，必须增加它
            imin = i + 1
        elif i > 0 and nums1[i-1] > nums2[j]:
            # i太大，必须减小它
            imax = i - 1
        else:
            # i正好
            if i == 0: max_of_left = nums2[j-1]
            elif j == 0: max_of_left = nums1[i-1]
            else: max_of_left = max(nums1[i-1], nums2[j-1])
            
            if (m + n) % 2 == 1:
                return max_of_left
            
            if i == m: min_of_right = nums2[j]
            elif j == n: min_of_right = nums1[i]
            else: min_of_right = min(nums1[i], nums2[j])
            
            return (max_of_left + min_of_right) / 2.0
    
    # 这种情况不应该发生，如果发生了说明输入有误
    raise ValueError("Input arrays are not sorted or other error occurred")

# 示例
print(findMedianSortedArrays([1,3], [2])) # 输出: 2.00000
print(findMedianSortedArrays([1,2], [3,4])) # 输出: 2.50000

这段代码首先确保了nums1是较短的数组，然后通过二分查找在nums1上找到一个合适的索引i，使得nums1的前i个元素和nums2的前j个元素共同构成了合并后数组的前一半。最后根据合并后数组长度的奇偶性来计算中位数。

Baichuan 4 (百川智能) 点评

我们看到，这里同样使用了python的解法，代码可运行，解法描述比较清晰，并且考虑到了错误处理，还是不错的。

ERNIE 4.0 8K 0329 (百度文心一言) 回答

要实现时间复杂度为 O(log(m+n)) 的算法来找到两个正序数组的中位数，可以使用二分查找的方法。但请注意，严格的 O(log(m+n)) 解决方案可能相当复杂。为了简化，如果我们允许一个稍微宽松的时间复杂度界限（例如，在某些情况下接近 O(log(min(m, n)))），我们可以采用一个更容易理解的方法。

下面是一个简化的方法，它基于二分查找，但并不是严格的 O(log(m+n))，而是更接近于 O(log(min(m, n)))，因为它每次都在较短的数组上进行二分操作：

def findMedianSortedArrays(nums1, nums2):
    if len(nums1) > len(nums2):
        nums1, nums2 = nums2, nums1  # 确保 nums1 是较短的数组
    m, n = len(nums1), len(nums2)
    left, right = 0, m
    while left <= right:
        partitionX = (left + right) // 2  # 在 nums1 中的分割点
        partitionY = ((m + n + 1) // 2) - partitionX  # 在 nums2 中的分割点

        # 确保左半部分都小于右半部分
        maxLeftX = float('-inf') if partitionX == 0 else nums1[partitionX - 1]
        minRightX = float('inf') if partitionX == m else nums1[partitionX]
        maxLeftY = float('-inf') if partitionY == 0 else nums2[partitionY - 1]
        minRightY = float('inf') if partitionY == n else nums2[partitionY]

        if maxLeftX <= minRightY and maxLeftY <= minRightX:
            # 已经找到了正确的划分
            if (m + n) % 2 == 0:
                return max(maxLeftX, maxLeftY, key=float) / 2 + min(minRightX, minRightY, key=float) / 2
            else:
                return max(maxLeftX, maxLeftY, key=float)  # 总是取较大的左半部分作为中位数

        elif maxLeftX > minRightY:  # 太靠右，需要向左调整
            right = partitionX - 1
        else:  # 太靠左，需要向右调整
            left = partitionX + 1
            
    # 如果未找到中位数，则抛出异常（实际上，由于我们的逻辑，这里不会被执行到）
    raise ValueError("No median found")

# 示例测试
print(findMedianSortedArrays([1, 3], [2]))  # 输出: 2.0
print(findMedianSortedArrays([1, 2], [3, 4]))  # 输出: 2.5

这个算法通过二分查找确定两个数组中的分割点，以确保左半部分的所有元素都小于或等于右半部分的所有元素。然后，根据分割点找到中位数。注意，这个解决方案在数组长度不等的情况下也能正确工作，并且处理了总数组长度是奇数还是偶数的情况。

虽然这个解决方案的时间复杂度并不是严格的 O(log(m+n))，但在很多实际应用中，它的性能已经足够好，并且比严格的 O(log(m+n)) 解决方案更容易理解和实现。如果需要严格的 O(log(m+n)) 解决方案，请参考一些高级的二分查找变种，它们通常涉及更复杂的边界条件和分割逻辑。

ERNIE 4.0 8K 0329 (百度文心一言) 点评

文心一言给的也是python的回答，可见python确实是比较常用。文心一言没有给出具体的算法步骤，但代码注释和中文描述都很流畅易懂，比百川智能要稍强一些。

Hunyuan Pro (腾讯混元) 回答

为了实现 O(log(m+n)) 的时间复杂度，我们可以使用二分查找的方法。首先，我们需要找到两个数组中较短的那个数组，并将其作为二分查找的主体。假设较短数组为 A，长数组为 B，我们可以在 A 中进行二分查找，找到一个位置 partitionA，使得 A 中有 partitionA 个元素在左侧，有 len(A) - partitionA 个元素在右侧。同时，我们需要在 B 中找到一个位置 partitionB，使得 B 中有 partitionB 个元素在左侧，有 len(B) - partitionB 个元素在右侧。这样，我们可以保证左侧的所有元素都小于等于右侧的所有元素。

接下来，我们需要判断当前的分割是否满足条件。如果满足条件，我们就可以计算中位数。如果不满足条件，我们需要根据实际情况调整二分查找的范围。

以下是具体的算法步骤：

  1. 找到较短的数组 A 和长数组 B。
  2. 初始化二分查找的范围：imin = 0，imax = len(A)。
  3. 进行二分查找：
    a. 计算 partitionA = (imin + imax) // 2。
    b. 计算 partitionB = (len(A) + len(B) + 1) // 2 - partitionA。
    c. 判断当前分割是否满足条件：
    • 如果 partitionA > 0 且 A[partitionA-1] > B[partitionB]，说明当前分割过于右侧，需要将 imax 更新为 partitionA - 1。
    • 如果 partitionA < len(A) 且 A[partitionA] < B[partitionB-1]，说明当前分割过于左侧，需要将 imin 更新为 partitionA + 1。
    • 否则，当前分割满足条件，可以计算中位数。
  4. 计算中位数：
    • 如果 (len(A) + len(B)) 是奇数，那么中位数为 max(A[partitionA-1], B[partitionB-1])。
    • 如果 (len(A) + len(B)) 是偶数，那么中位数为 (max(A[partitionA-1], B[partitionB-1]) + min(A[partitionA], B[partitionB])) / 2。

以下是 Python 代码实现：

def findMedianSortedArrays(nums1, nums2):
    if len(nums1) > len(nums2):
        nums1, nums2 = nums2, nums1

    m, n = len(nums1), len(nums2)
    imin, imax, half_len = 0, m, (m + n + 1) // 2

    while imin <= imax:
        partitionA = (imax + imin) // 2
        partitionB = half_len - partitionA

        if partitionA > 0 and nums1[partitionA - 1] > nums2[partitionB]:
            imax = partitionA - 1
        elif partitionA < m and nums2[partitionB - 1] > nums1[partitionA]:
            imin = partitionA + 1
        else:
            if partitionA == 0:
                max_of_left = nums2[partitionB - 1]
            elif partitionB == 0:
                max_of_left = nums1[partitionA - 1]
            else:
                max_of_left = max(nums1[partitionA - 1], nums2[partitionB - 1])

            if (m + n) % 2 == 1:
                return max_of_left

            if partitionA == m:
                min_of_right = nums2[partitionB]
            elif partitionB == n:
                min_of_right = nums1[partitionA]
            else:
                min_of_right = min(nums1[partitionA], nums2[partitionB])

            return (max_of_left + min_of_right) / 2

这个算法的时间复杂度为 O(log(min(m, n)))，满足题目要求。

Hunyuan Pro (腾讯混元) 点评

腾讯混元给出了具体的思路和具体步骤，并给出了常规的python解答，还是不错的。

Mixtral 8x22B Instruct (Mistral) 回答

这个问题可以使用二分查找的思想来解决。

首先，我们需要找到两个数组的中位数，如果两个数组的长度之和为奇数，那么中位数就是中间那个数，如果为偶数，那么中位数就是中间两个数的平均值。

我们可以定义两个指针，分别指向两个数组的开头，然后我们可以不断地比较这两个指针所指向的数，将较小的那个数放入一个新的数组中，直到我们找到中位数。

具体实现如下：

def findMedianSortedArrays(nums1, nums2):
    nums = nums1 + nums2
    nums.sort()
    length = len(nums)
    if length % 2 == 0:
        return (nums[length // 2] + nums[length // 2 - 1]) / 2
    else:
        return nums[length // 2]

这个实现的时间复杂度是 O(m+n)，因为我们需要将两个数组合并成一个数组，然后排序，最后找到中位数。但是这个实现并不满足题目要求的时间复杂度为 O(log(m+n))。

为了满足题目要求的时间复杂度，我们可以使用二分查找的思想。具体实现如下：

def findMedianSortedArrays(nums1, nums2):
    if len(nums1) > len(nums2):
        nums1, nums2 = nums2, nums1
    x, y = len(nums1), len(nums2)
    start = 0
    end = x
    while start <= end:
        partitionX = (start + end) // 2
        partitionY = ((x + y + 1) // 2) - partitionX
        maxLeftX = float('-inf') if partitionX == 0 else nums1[partitionX - 1]
        minRightX = float('inf') if partitionX == x else nums1[partitionX]
        maxLeftY = float('-inf') if partitionY == 0 else nums2[partitionY - 1]
        minRightY = float('inf') if partitionY == y else nums2[partitionY]
        if maxLeftX <= minRightY and maxLeftY <= minRightX:
            if (x + y) % 2 == 0:
                return max(maxLeftX, maxLeftY), min(minRightX, minRightY)
            else:
                return max(maxLeftX, maxLeftY)
        elif maxLeftX > minRightY:
            end = partitionX - 1
        else:
            start = partitionX + 1

这个实现的时间复杂度是 O(log(min(m, n)))，因为我们使用二分查找的思想，每次都将问题规模减半。

这个实现的基本思想是，我们需要找到两个数组的中位数，因此我们需要将这两个数组分成两部分，使得左半部分的最大值小于等于右半部分的最小值。如果左半部分的最大值大于右半部分的最小值，那么我们就需要将分割点向左移动，否则我们就需要将分割点向右移动。

当我们找到了分割点后，我们就可以根据两个数组的长度来判断中位数是左半部分的最大值还是右半部分的最小值。如果两个数组的长度之和为奇数，那么中位数就是左半部分的最大值，如果为偶数，那么中位数就是左半部分的最大值和右半部分的最小值的平均值。

Mixtral 8x22B Instruct (Mistral) 点评

Mistral给出了两个思路，并且给出了对应代码的解析，中文描述也很流畅。对于这个我不是很熟的模型，我感觉还是不错的。

Qwen Max 0428 (阿里通义千问)回答

这个问题可以通过使用二分查找算法来解决，以达到O(log(min(m, n)))的时间复杂度，而不是题目要求的O(log(m+n))，但这是解决此问题最有效的方法。下面是详细的解决方案：

首先，确定哪个数组作为“较小”的数组可以简化问题。我们希望在两个数组之间进行相等划分，因此将较小的数组作为分割操作的目标会更高效。如果m > n，就交换两个数组，确保nums1是两个数组中较小或相等的那个。

然后，我们定义一个函数findKthElement用来寻找两个已排序数组中的第k小元素。这个函数的核心思想是使用二分查找法在nums1数组上找到一个位置i，使得nums1[i-1] <= nums2[k-i] && nums2[k-i-1] <= nums1[i]。这样，第k小的元素要么是nums1[i]，要么是nums2[k-i]，具体取决于它们的相对位置和值。

以下是该算法的Python实现：

def findMedianSortedArrays(nums1, nums2):
    # 确保nums1是较短的数组
    if len(nums1) > len(nums2):
        nums1, nums2 = nums2, nums1
        
    x, y = len(nums1), len(nums2)
    low, high = 0, x
    
    while low <= high:
        partitionX = (low + high) // 2
        partitionY = (x + y + 1) // 2 - partitionX
        
        # 如果partitionX是0，说明我们已经超出了nums1的左侧边界，此时nums1[-1]相当于一个负无穷
        maxLeftX = float('-inf') if partitionX == 0 else nums1[partitionX - 1]
        # 类似地处理nums1的右侧边界
        minRightX = float('inf') if partitionX == x else nums1[partitionX]
        
        maxLeftY = float('-inf') if partitionY == 0 else nums2[partitionY - 1]
        minRightY = float('inf') if partitionY == y else nums2[partitionY]
        
        if maxLeftX <= minRightY and maxLeftY <= minRightX:
            # 找到了正确的分区
            if (x + y) % 2 == 0:
                # 数组总长度为偶数
                return max(maxLeftX, maxLeftY), min(minRightX, minRightY)
            else:
                # 数组总长度为奇数
                return max(maxLeftX, maxLeftY)
        elif maxLeftX > minRightY:
            # 缩小nums1的右边界
            high = partitionX - 1
        else:
            # 扩大nums1的左边界
            low = partitionX + 1
            
    # 上述逻辑应始终能找到答案，理论上不会执行到这一步
    return None

这段代码实现了寻找两个有序数组中位数的功能，符合题目要求。注意，虽然这里的解释提到时间复杂度为O(log(min(m, n)))，但实际解决问题的思路是正确的，且效率较高，满足题目的实际需求。

Qwen Max 0428 (阿里通义千问)点评

通义千问这个大家都比较熟悉了，它给出了思路和代码，并且代码有注释，但没有给测试用例，整体还是不错的。

测评总结

在这道题上，文中的各个模型都给出了不错的回答。从整体上来看，以下是各个模型在我心目中的排名：

  1. Mistral
  2. Qwen Max 0428
  3. 腾讯混元
  4. 百度文心一言
  5. MiniMax
  6. 百川智能

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1720671.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Day-04python模块

Day-04python模块

一、模块 1-1 Python 自带模块 Json模块 处理json数据 {"key":"value"} json不是字典 本质是一个有引号的字符串数据 json注意点 {} 中的数据是字符串引号必须是双引号 使用json模块可以实现将json转为字典&#xff0c;使用字典的方法操作数据 。 或者将…
阅读更多...
HCIP-Datacom-ARST自选题库__MAC【14道题】

HCIP-Datacom-ARST自选题库__MAC【14道题】

一、单选题 1.缺省情况下&#xff0c;以下哪种安全MAC地址类型在设备重启后表项会丢失? 黑洞MAC地址 Sticky MAC地址 安全动态MAC地址 安全静态MAC地址 2.华为交换机MAC地址表中的动态sticky MAC地址的默认老化时间是多少秒? 300 不会老化 400 500 3.华为交换机MA…
阅读更多...
apache大数据各组件部署搭建（超级详细）

apache大数据各组件部署搭建（超级详细）

apache大数据数仓各组件部署搭建 第一章 环境准备 1. 机器规划 准备3台服务器用于集群部署，系统建议CentOS7+，2核8G内存 172.19.195.228 hadoop101 172.19.195.229 hadoop102 172.19.195.230 hadoop103 [root@hadoop101 ~]# cat /etc/redhat-release CentOS Linux rele…
阅读更多...
揭秘APP广告变现项目

揭秘APP广告变现项目

在当今移动应用市场&#xff0c;广告变现已经成为开发者盈利策略的重要组成部分。 通过在应用程序中展示多种类型的广告&#xff0c;如插页式广告、横幅广告和激励视频广告&#xff0c;开发者能够获得经济效益。 实现这一目标的核心在于平衡收入与用户体验&#xff0c;避免过…
阅读更多...
【差分隐私联邦学习从入门到发文】

【差分隐私联邦学习从入门到发文】

差分隐私联邦学习从入门到发文 差分隐私联邦学习从入门到发文一、学习相关理论1. 差分隐私理论解读2. 联邦学习相关收敛性分析3. 差分隐私经典论文解读4. 联邦学习代码解读5. 深度学习相关代码网站 二、必读论文三、最新进展2023 差分隐私联邦学习从入门到发文 这是关于差分隐…
阅读更多...
虚拟现实环境下的远程教育和智能评估系统（五）

虚拟现实环境下的远程教育和智能评估系统（五）

查阅相关VR眼动注意力联合教育学相关论文 1.Exploring Eye Gaze Visualization Techniques for Identifying Distracted Students in Educational VR&#xff08;IEEE VR 2020&#xff09; 摘要&#xff1a;我们提出了一种架构&#xff0c;使VR教学代理能够响应眼动追踪监控…
阅读更多...
校园交友|基于SprinBoot+vue的校园交友网站(源码+数据库+文档)

校园交友|基于SprinBoot+vue的校园交友网站(源码+数据库+文档)

校园交友网站 目录 基于SprinBootvue的校园交友网站 一、前言 二、系统设计 三、系统功能设计 1系统功能模块 2后台功能模块 5.2.1管理员功能模块 5.2.2用户功能模块 四、数据库设计 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐 八、源码获取&#x…
阅读更多...
2024年四川省三支一扶报名照片上传成功啦

2024年四川省三支一扶报名照片上传成功啦

2024年四川省三支一扶报名照片上传成功&#xff0c;一定要下载照片审核工具哦&#xff0c;详情如下图所示
阅读更多...
【设计模式】创建型-建造者模式

【设计模式】创建型-建造者模式

前言 在面向对象的软件开发中&#xff0c;构建复杂对象时经常会遇到许多挑战。一种常见的解决方案是使用设计模式&#xff0c;其中建造者模式是一个强大而灵活的选择。本文将深入探讨建造者模式的原理、结构、优点以及如何在实际项目中应用它。 一、复杂的对象 public class…
阅读更多...
ARM虚拟机安装OMV

ARM虚拟机安装OMV

OMV(OpenMediaVault)是基于 Debian GNU/Linux 的网络连接存储&#xff08;network attached storage&#xff0c;NAS&#xff09;解决方案。它包含 SSH、(S) FTP、SMB/CIFS、DAAP 媒体服务器、rsync、 BitTorrent 等很多种服务。它可用于 x86-64 和 ARM 平台。 在x86-64平台上&…
阅读更多...
小学数学出题器-Word插件-大珩助手

小学数学出题器-Word插件-大珩助手

Word大珩助手是一款功能丰富的Office Word插件&#xff0c;旨在提高用户在处理文档时的效率。它具有多种实用的功能&#xff0c;能够帮助用户轻松修改、优化和管理Word文件&#xff0c;从而打造出专业而精美的文档。 【新功能】小学数学出题器 1、实现了难度设定&#xff1b;…
阅读更多...
[每周一更]-(第99期)：MySQL的索引为什么用B+树？

[每周一更]-(第99期)：MySQL的索引为什么用B+树？

文章目录 B树与B树的基本概念B树&#xff08;Balanced Tree&#xff09;B树&#xff08;B-Plus Tree&#xff09;对比 为什么MySQL选择B树1. **磁盘I/O效率**2. **更稳定的查询性能**3. **更高的空间利用率**4. **并发控制** 其他树结构的比较参考 索引是一种 数据结构&#x…
阅读更多...
笔记-docker基于ubuntu22.04安装Jitsi Meet

笔记-docker基于ubuntu22.04安装Jitsi Meet

背景 利用JitsiMeet打造一个可以在线会议的环境&#xff0c;根据躺的坑&#xff0c;做个记录 参考 JitsMeet部署安装说明 开始操作 环境 docker run -it --name ubuntu22.04 ubuntu:22.04 /bin/bash问题 1、安装 openjdk-11 apt install openjdk-11-jdk配置环境变量&…
阅读更多...
Arduino RP2040 CDC虚拟串口通讯--普通串口不显示

Arduino RP2040 CDC虚拟串口通讯--普通串口不显示

这两天在用RP2040运行些程序&#xff0c;但发现一个问题&#xff0c;使用arduino IDE可以通过串口显示数据&#xff0c;但是其他串口工具不会显示数据&#xff0c;可以打开串口&#xff0c;排查一下午无果&#xff0c;相当头疼&#xff0c; 晚上搜索时发现这个介绍&#xff1a…
阅读更多...
strcpy、strncpy、strcat、strncat、strcmp、strstr字符串函数的使用和模拟

strcpy、strncpy、strcat、strncat、strcmp、strstr字符串函数的使用和模拟

strcpy的使用和模拟&#xff08;作用&#xff09; 将一个字符串的内容复制到另外一个字符串中代替掉。 strcpy的使用效果 #include <stdio.h> #include <string.h>int main () {char str1[]"Sample string";char str2[40];char str3[40];strcpy (str2…
阅读更多...
使用pytorch搭建textCNN、BERT、transformer进行文本分类

使用pytorch搭建textCNN、BERT、transformer进行文本分类

首先展示数据处理后的类型&#xff1a; 第一列为文本&#xff0c;第二类为标注的标签&#xff0c;数据保存在xlsx的表格中&#xff0c;分为训练集和验证集。 textCNN 直接上整个工程代码&#xff1a; import pandas as pd import numpy as np import torch from torch.util…
阅读更多...
Java排序算法汇总篇，八种排序算法

Java排序算法汇总篇，八种排序算法

排序算法汇总: Java排序算法(一)&#xff1a;冒泡排序 Java排序算法(二)&#xff1a;选择排序 Java排序算法(三)&#xff1a;插入排序 Java排序算法(四)&#xff1a;快速排序 Java排序算法(五)&#xff1a;归并排序 Java排序算法(六)&#xff1a;希尔排序 Java排序算法(…
阅读更多...
vm-bhyve网卡设定桥接故障解决@FreeBSD

vm-bhyve网卡设定桥接故障解决@FreeBSD

问题 在使用vm-bhyve虚拟机管理软件的时候&#xff0c;使用vm无法绑定网卡igb0 vm switch add public igb0 报错&#xff1a;/usr/local/sbin/vm: ERROR: failed to add member igb0 to the virtual switch public 解决 于是准备用原生ifconfig命令来绑定&#xff0c;结果…
阅读更多...
Pytorch的学习

Pytorch的学习

1.基本数据&#xff1a;Tensor Tensor&#xff0c;即张量&#xff0c;是PyTorch中的基本操作对象&#xff0c;可以看做是包含单一数据类型元素的多维矩阵。从使用角度来看&#xff0c;Tensor与NumPy的ndarrays非常类似&#xff0c;相互之间也可以自由转换&#xff0c;只不过Te…
阅读更多...
六一儿童节与AIGC：科技与童趣的奇妙融

六一儿童节与AIGC：科技与童趣的奇妙融

随着人工智能生成内容&#xff08;AIGC&#xff09;技术的发展&#xff0c;越来越多的应用和网站专门为儿童提供学习、游戏和绘画方面的支持。这些平台不仅能够提高孩子们的学习兴趣&#xff0c;还能激发他们的创造力。在六一儿童节即将到来之际&#xff0c;让我们来介绍几款利…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023