一、正则表达式到NFA的基本结构

1. 我们先回顾一下 RE 的三个基本操作：

• 可选（alternative）：对于给定的两个正则表达式 M 和 N，选择操作符（ | ）形成一个新的正则表达式 M|N ，如果一个字符串属于 M 或者 N，则它属于 M|N。
• 联结（concatenation）：对于两个对于给定了两个正则表达式 M 和 N，连接操作符（ · ）形成一个新的正则表达式 M·N，通常可以省略连接符号，比如 (a|b)·a ，定义了两个字符串：aa、ab。
• 克林闭包（Kleene closure）： 正则表达式 M 的克林闭包，记作 M*，定义为 M 与自身连接 0 次或者多次形成的所有集合取并集。

2. RE 到 NFA

由于 NFA 是 RE 的实现形式，本身是等价，我们先看看三个基本操作对应的 NFA ，这里我们介绍一下 Thompson 构造法：

这个构造法包含三个基本操作以及单个字符对应的 NFA:

• a 对应的 NFA
  

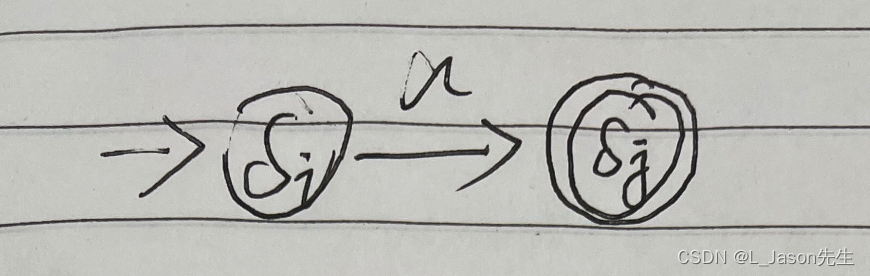
• b 对应的 NFA
  

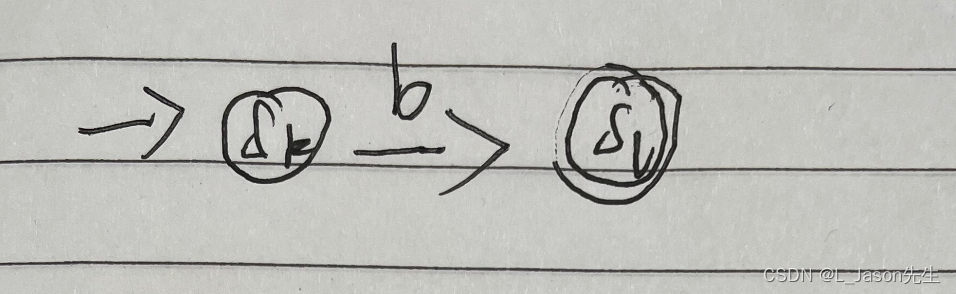
• ab 对应的 NFA
  

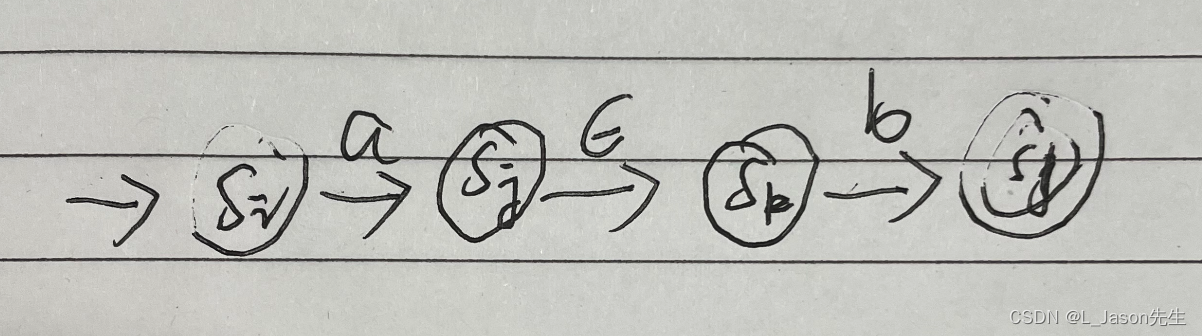
• a|b 对应的NFA
  

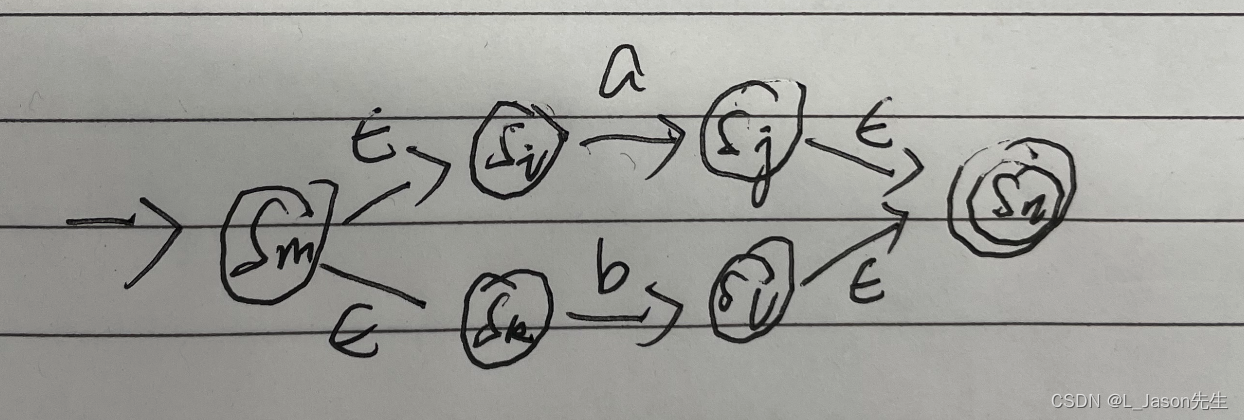
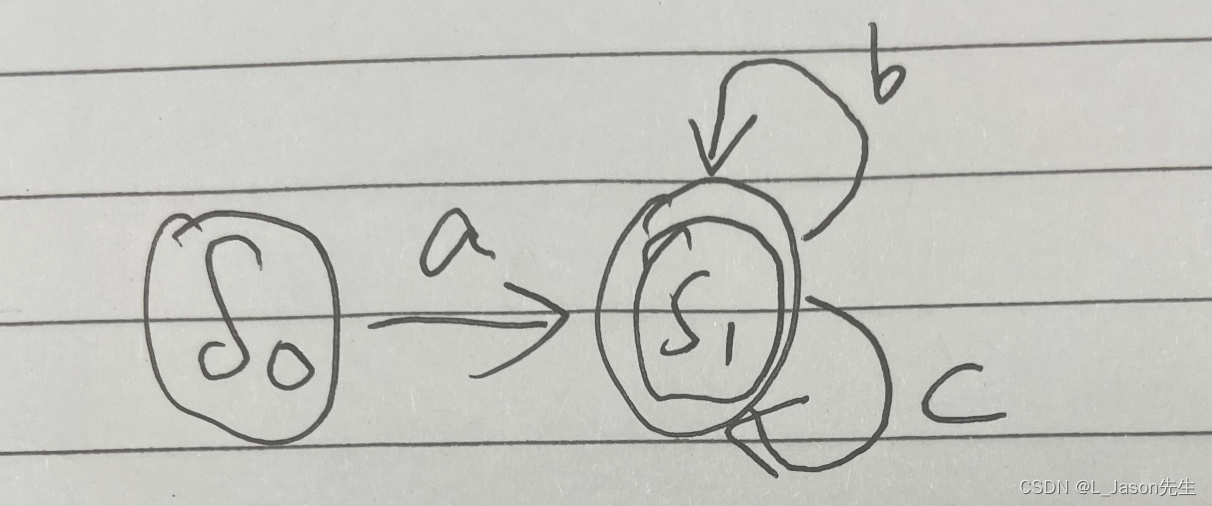
• a* 对应的 NFA
  

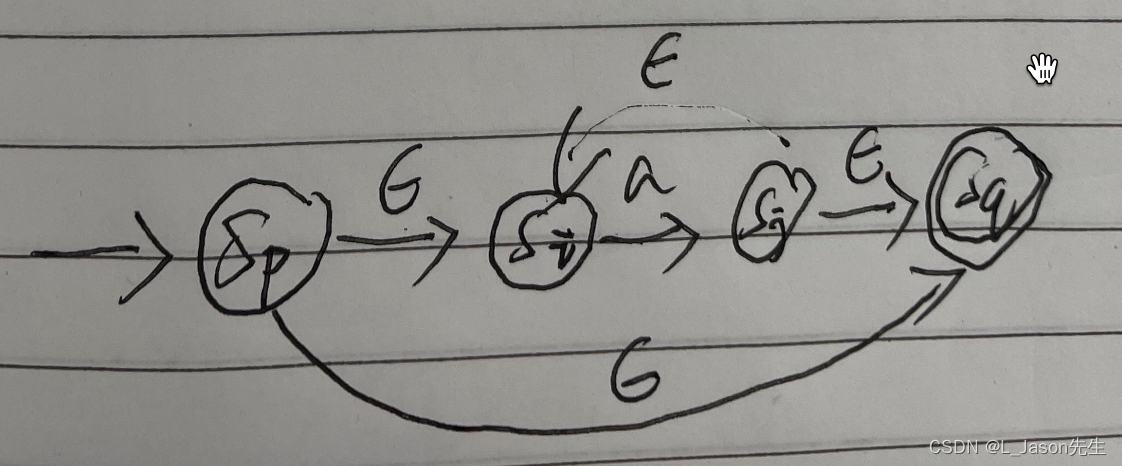
注：带有双环的状态属于接受状态

这个构造发就是从输入的 RE 每一个字符构造简单的 NFA 开始，然后按照优先级规定的顺序，根据基本操作转换的。

这种构造法实现起来比较简单，每个NFA 都有一个 S(0) 和一个 S(A)，没有从 S(A) 发出的转移，连接其他 NFA 的时候总是使用 ϵ 转移来链接前一个 NFA 的 S(A)和后一个 NFA 的起始状态。最后，每个状态至多有两个进入或者退出该状态的 ϵ 转移。对于字母表中的每个符号，至多有一个进入该状态和退出该状态的转移。这些性质简化了 NFA 的表示以及操作

3. 举例介绍

我们根据 Thompson 构造法，分步骤构造一下 a(b|c)* 这个正则表达式的转化过程

1. 对字母表中的 a、b、c 构造对应单个字符对应的 NFA
   

2. 构造出 b|c 对应 的 NFA
   

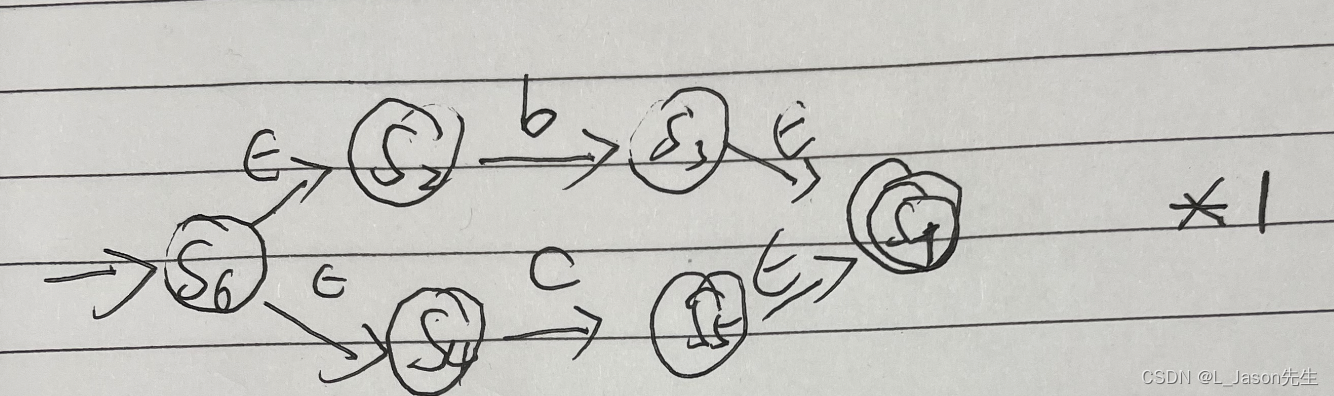
3. 构造出 (b|c)* 对应的 NFA，对 *1 这个 NFA，执行克林闭包的基本操作：
   

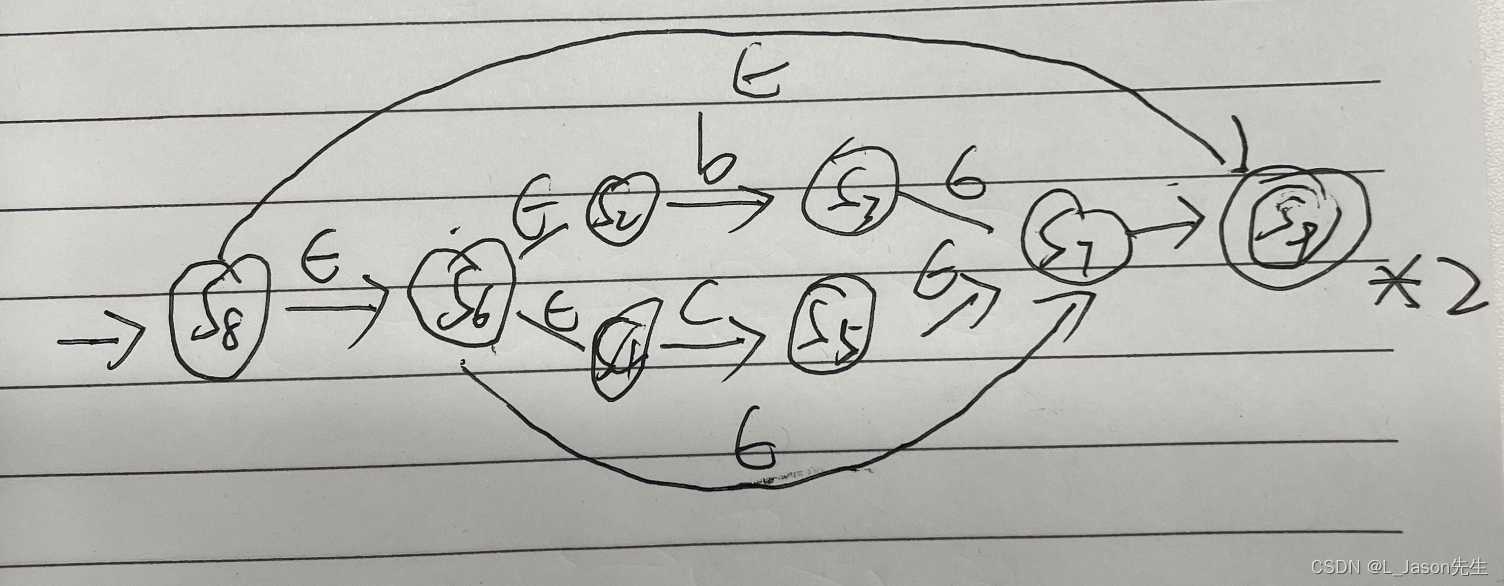
4. 在 2 式前面进行连接 a 的基本操作，完成最终的转化， 2 式代表(b|c) 的 NFA
   

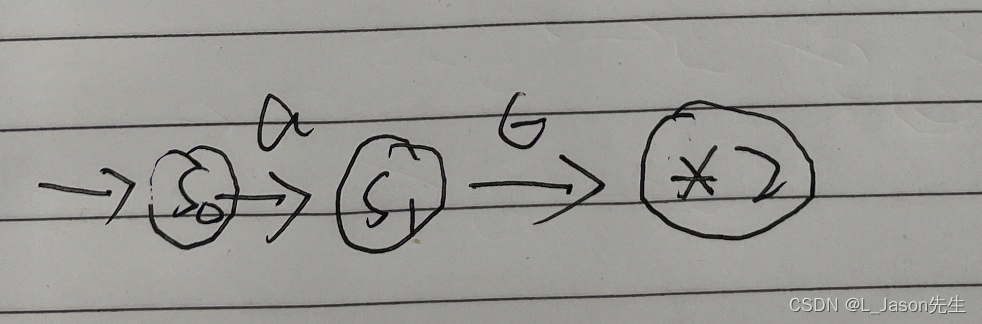
5. 其实上面的例子可以看到 NFA 存在大量的不必要的状态以及 ϵ 转移，这些都可以通过一些 NFA 转化为 DFA 的构造方法，比如子集构造法，将这些无效的状态转移移除，最终形成的 DFA 如下：