目录
1.Docker服务管理命令:
启动:systemctl start docker
停止:systemctl stop docker
重启:systemctl restart docker
开机自启:systemctl enable docker
查看docker版本:
2.镜像常用管理命令:
搜索镜像:
镜像拉取下载:
列出本地所有镜像
删除本地镜像
将本地镜像保存为本地文件
4.添加新标签(更改镜像名称)
为镜像添加多个名称和标签
将文件导入到本地镜像
镜像上传
3.Docker容器常用管理命令
查看容器详细信息
(2)查看正在运行的容器
查看所有容器
(3)启动容器
关闭容器
查看容器状态
(4)创建并启用容器
(5)进入运行中的容器
(6)导出容器
(7)导入容器
(8)查看容器日志
动态查看容器日志
(8)删除容器
(9)从宿主机上传下载到容器
宿主机文件上传至容器
将容器里的文件下载到宿主机
按容器名进行删除
按id号进行删除
1.Docker服务管理命令:
启动:systemctl start docker
停止:systemctl stop docker
重启:systemctl restart docker
开机自启:systemctl enable docker
查看docker版本:
docker -v
docker version #相比于-v此命令会更详细的显示
2.镜像常用管理命令:
搜索镜像:
docker search centos
镜像拉取下载:
docker pull contos:7
列出本地所有镜像
docker images(常用)或使用docker image ls
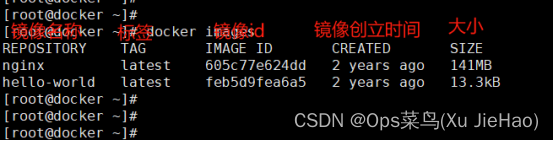
删除本地镜像
docker rmi -f 名称:标签或使用镜像的id号 #选项-f为强制删除
将本地镜像保存为本地文件
docker save名称:标签 > 镜像文件名称

4.添加新标签(更改镜像名称)
为镜像添加多个名称和标签
命令语法:docker tag 名称:标签 新名称:新标签
[root@localhost ~]# docker tag nickistre/centos-lamp:latest centos:lamp
[root@localhost ~]# docker images //查看镜像
//名称与标签可以添加多个,ID号是唯一的
将文件导入到本地镜像
docker load < 镜像文件
镜像上传
//本地存储的镜像越来越多,就需要指定一个专门的地方存放这些镜像—仓库(后续会详细讲到)
命令格式:docker push 名称:标签
docker push guyton/centos7:latest
3.Docker容器常用管理命令
查看容器详细信息
docker inspect 0d311d
(1)创建容器
命令格式:docker create [选项] 镜像 运行的程序
选项:
-i 让容器的标准输入保持打开
-t 让Docker分配一个伪终端
docker create -it centos:ly
(2)查看正在运行的容器
docker ps
查看所有容器
docker ps -a

解释:
CONTAINER ID:容器的ID号(唯一的)
IMAGE:加载的镜像
COMMAND:运行的程序
CREATED:创建时间
STATUS:目前所处的状态
PORTS:端口映射
(3)启动容器
docker start 镜像id或名称
关闭容器
docker stop 镜像id或名称
查看容器状态
docker stats 镜像id或名称

(4)创建并启用容器
命令格式:docker run [选项] 镜像 运行的程序
等同于先执行docker create命令,再执行docker start命令。需要注意只要后面的命令运行结束,容器就会停止。
docker run centos:ly /bin/bash -c ls /
//创建容器的并启动执行一条shell命令,命令完成容器就停止
创建容器并启动执行shell命令
选项:
-d 在后台进行运行
--name 指定新创建的容器名称
(5)进入运行中的容器
命令格式:docker exec –it 容器ID/名称 /bin/bash
docker exec -it 7708 /bin/bash
(6)导出容器
导出:将已经创建好的容器导出为文件,无论这个容器是处于运行状态还是停止状态均可导出。
命令格式:docker export 容器ID/名称 > 文件名
[root@localhost ~]# docker export 6e22920fc447 > centostar
(7)导入容器
将容器文件生成镜像
命令格式:cat 文件名 | docker import – 生成的镜像名称:标签
[root@localhost ~]# cat centostar | docker import - centos1:latest
(8)查看容器日志
docker logs 77088
动态查看容器日志
docker logs --tail -f20 77088
选项:
--tail 查看结尾
-f 动态输出
(8)删除容器
命令格式:docker rm 容器ID/名称
Docker rm –f 容器ID/名称 //强制删除运行中的容器,不建议使用-f
(9)从宿主机上传下载到容器
宿主机文件上传至容器
[root@docker ~]# docker cp test01.txt 7708:/
Successfully copied 1.54kB to 7708:/
将容器里的文件下载到宿主机
[root@docker ~]# docker cp 容器id或名称:/etc/hosts /opt
按容器名进行删除
docker rm -f nginx
按id号进行删除
docker rm -f 9a78