2023牛客寒假算法基础集训营2(11/12)

news2024/9/22 13:42:34

Tokitsukaze and a+b=n (easy)

Tokitsukaze and a+b=n (medium)

要使a+b=n，那么转换一下就是b=n-a，所以只需要计算[n-L,n-R]和[L',R']相交的部分即可

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    while (T--) {
        LL n;
        cin >> n;
        LL l1, l2, r1, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if (l1 > n || l2 > n) {
            cout << "0\n";
            continue;
        }
        if (r1 + r2 < n) {
            cout << "0\n";
            continue;
        }
        l1 = max(0LL, n - l1);
        r1 = max(0LL, n - r1);
        if (l1 > r1) {
            swap(l1, r1);
        }
        if (l1 >= l2) {
            if (l1 <= r2) {
                cout << min(r2, r1) - l1 + 1 << '\n';
            } else {
                cout << "0\n";
            }
        } else {
            if (r1 < l2) {
                cout << "0\n";
            } else {
                cout << min(r1, r2) - l2 + 1 << '\n';
            }
        }
    }
    return 0;
}

Tokitsukaze and a+b=n (hard)

先运用差分数组c标记[L,R],再算差分数组的前缀和，即为每个点被区间覆盖了多少次，然后再算前缀和的前缀和，即为从1~i点一共被覆盖了多少次，计算有多少a+b=n，即计算[min(n-L,n-R),max(n-L,n-R)]=[L',R']区间覆盖次数，即为求presum[R']-presum[L'-1]再减去[L,R]和[L',R']重叠的部分

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
const int mod = 998244353;
int c[400010], presum[400010], presum1[400010];
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, m;
    cin >> n >> m;
    vector<pair<int, int>> a(m + 1);
    for (int i = 1; i <= m; i++) {
        cin >> a[i].first >> a[i].second;
        c[a[i].first]++;
        c[a[i].second + 1]--;
    }
    for (int i = 1; i <= 400005; i++) {
        presum[i] = (presum[i - 1] + c[i]) % mod;
        presum1[i] = (presum1[i - 1] + presum[i]) % mod;
    }
    LL ans = 0;
    for (int i = 1; i <= m; i++) {
        pair<int, int> b;
        b.first = n - a[i].first;
        b.second = n - a[i].second;
        if (b.first > b.second) {
            swap(b.first, b.second);
        }
        if (b.second < 1) {
            continue;
        }
        if (b.first < 1) {
            b.first = 1;
        }
        if (a[i].second < b.first) {

        } else if (a[i].first > b.second) {

        } else if (a[i].first >= b.first && a[i].second <= b.second) {
            ans = (ans - (a[i].second - a[i].first + 1) + mod) % mod;
        } else if (b.first >= a[i].first && b.second <= a[i].second) {
            ans = (ans - (b.second - b.first + 1) + mod) % mod;
        } else if (b.first <= a[i].first && b.second <= a[i].second && a[i].first <= b.second) {
            ans = (ans - (b.second - a[i].first + 1) + mod) % mod;
        } else if (a[i].first <= b.first && a[i].second <= b.second && b.first <= a[i].second) {
            ans = (ans - (a[i].second - b.first + 1) + mod) % mod;
        }
        ans = (ans + presum1[b.second] - presum1[b.first - 1] + mod) % mod;
    }
    cout << (ans + mod) % mod << '\n';
    return 0;
}

Tokitsukaze and Energy Tree

根据题意贪心可知，能量越多的应该放在越深的节点上，这样到根的距离最长，计算次数最多

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;
    cin >> n;
    vector<vector<int>> G(n + 1);
    for (int i = 2; i <= n; i++) {
        int u;
        cin >> u;
        G[i].push_back(u);
        G[u].push_back(i);
    }
    vector<LL> a(n + 1), b(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a.begin() + 1, a.end(), [&](LL x, LL y) {
        return x > y;
    });
    vector<pair<int, int>> dep(n + 1);
    function<void(int, int)> dfs = [&](int u, int fa) {
        dep[u].first = dep[fa].first + 1;
        dep[u].second = u;
        for (auto v: G[u]) {
            if (v != fa) {
                dfs(v, u);
            }
        }
    };
    dfs(1, 0);
    sort(dep.begin() + 1, dep.end(), [&](pair<int, int> x, pair<int, int> y) {
        if (x.first != y.first) {
            return x.first > y.first;
        }
        return x.second > y.second;
    });
    for (int i = 1; i <= n; i++) {
        b[dep[i].second] = a[i];
    }
    vector<LL> sum(n + 1);
    LL ans = 0;
    function<void(int, int)> dfs1 = [&](int u, int fa) {
        sum[u] = b[u];
        for (auto v : G[u]) {
            if (v != fa) {
                dfs1(v, u);
                sum[u] = sum[u] + sum[v];
            }
        }
        ans = ans + sum[u];
    };
    dfs1(1, 0);
    cout << ans << '\n';
    return 0;
}

Tokitsukaze and Function

根据式子发现f(x)=n/x+x-1，可以令g(x)=n/x+x，根据均值不等式可知g(x)>=2sqrt(n)，当且仅当n/x=x时成立，所以我们就找到了g(x)最小值的一个取值点，因为f(x)中n/x为下取整，所以根据数论分块可知，最小值会是一段，而不再是某一个点，因此需要判断sqrt(n),sqrt(n)+1是否在[l,r]中，因为g(x)为对勾函数，所以还需要判断两个端点l,r是否取值更小，然后就是固定左端点l，右端点为l,r,sqrt(n),sqrt(n+1)其中之一，二分查找最小的x使得f(x)最小

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    while (T--) {
        LL n, l, r;
        cin >> n >> l >> r;
        LL m = sqrt(n), m1 = sqrt(n) + 1;
        LL pos = l, minn = 5e18;
        if (n / m + m - 1 < minn && m >= l && r >= m) {
            pos = m;
            minn = n / m + m - 1;
        }
        if (n / m1 + m1 - 1 < minn && m1 >= l && r >= m1) {
            pos = m1;
            minn = n / m1 + m - 1;
        }
        if (n / l + l - 1 < minn) {
            pos = l;
            minn = n / l + l - 1;
        }
        if (n / r + r - 1 < minn) {
            pos = r;
            minn = n / r + r - 1;
        }
        LL L = l, R = pos;
        while (L + 1 < R) {
            LL mid = (L + R) >> 1;
            if (n / mid + mid - 1 == minn) {
                R = mid;
            } else {
                L = mid;
            }
        }
        if (n / L + L - 1 == minn) {
            cout << L << '\n';
        } else {
            cout << R << '\n';
        }
    }
    return 0;
}

Tokitsukaze and Gold Coins (easy)

由题意可知需要保存k次操作后的地图，然后BFS从(1,1)跑一遍，标记能跑到的位置，再BFS从(n,3)跑一遍，标记能跑到的位置，如果(1,1)和(n,3)相互可达，那么两者都能跑到的即为能捡到的金币数

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int dx[] = {1, 0};
int dy[] = {0, 1};
int dx1[] = {-1, 0};
int dy1[] = {0, -1};
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    while (T--) {
        int n, k;
        cin >> n >> k;
        vector<vector<int>> G(n + 1, vector<int> (4));
        for (int i = 1; i <= k; i++) {
            int x, y;
            cin >> x >> y;
            G[x][y] ^= 1;
        }
        vector<vector<bool>> vis(n + 1, vector<bool> (4)), vis1(n + 1, vector<bool> (4));
        function<bool(int, int)> check = [&](int x, int y) {
            if (x < 1 || x > n || y < 1 || y > 3) {
                return false;
            }
            return true;
        };
        queue<pair<int, int>> q;
        q.push(make_pair(1, 1));
        while (!q.empty()) {
            pair<int, int> now = q.front();
            q.pop();
            for (int i = 0; i < 2; i++) {
                pair<int, int> nxt;
                nxt.first = now.first + dx[i];
                nxt.second = now.second + dy[i];
                if (check(nxt.first, nxt.second) && G[nxt.first][nxt.second] != 1 && !vis[nxt.first][nxt.second]) {
                    q.push(nxt);
                    vis[nxt.first][nxt.second] = 1;
                }
            }
        }
        if (!vis[n][3]) {
            cout << "0\n";
            continue;
        }
        q.push(make_pair(n, 3));
        vis1[n][3] = true;
        int ans = 0;
        while (!q.empty()) {
            pair<int, int> now = q.front();
            q.pop();
            for (int i = 0; i < 2; i++) {
                pair<int, int> nxt;
                nxt.first = now.first + dx1[i];
                nxt.second = now.second + dy1[i];
                if (check(nxt.first, nxt.second) && G[nxt.first][nxt.second] != 1 && !vis1[nxt.first][nxt.second]) {
                    q.push(nxt);
                    vis1[nxt.first][nxt.second] = 1;
                }
            }
        }
        if (!vis1[1][1]) {
            cout << "0\n";
            continue;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= 3; j++) {
                if (vis1[i][j] && vis[i][j]) {
                    ans++;
                }
            }
        }
        cout << ans << '\n';
    }
    return 0;
}

Tokitsukaze and K-Sequence

根据题意，把序列分成k段，容易想到出现次数小于等于k的数均分到各个子序列中，每个数都能产生1点影响，那么出现次数大于k的数，贪心地考虑就是k-1个平均分到k-1个区间内，剩下多余的全部扔到最后一个区间内，产生的影响就是(k-1)

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        vector<int> a(n + 1), cnt(n + 1);
        map<int, int> mp;
        for (int i = 1; i <= n; i++) {
            cin >> a[i];
            mp[a[i]]++;
        }
        LL sum = 0, sum1 = 0, ans = 0;
        for (auto it : mp) {
            cnt[it.second]++;
        }
        for (int i = 1; i <= n; i++) {
            sum += cnt[i];
        }
        for (int i = 1; i <= n; i++) {
            sum1 += cnt[i];
            ans += cnt[i] * i;
            cout << ans + (sum - sum1) * (i - 1) << '\n';
        }
    }
    return 0;
}

Tokitsukaze and Musynx

根据题意每个x[i]当且仅当有五种分数，而且也就只能发生4次分数的变化，所以一共是4*n，因此可以将x的坐标轴全部偏移到a的左边，这样所有的得分就是v[1]，然后用multiset自动排序，pair记录，pair的key就是x[i]偏移到下个分数段的最左侧需要多少，val就是下个分数段和当前分数段的差值，因为排序是key从小到大排，那么肯定是从最先到达下各分数段的开始变化，所以不会出现x[i]到了下个分数段而有其他数跳过了多个分数段的情况，所以每次加上分数变化的差值，记录其中的最大值即可

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        vector<LL> x(n + 1);
        for (int i = 1; i <= n; i++) {
            cin >> x[i];
            x[i] -= 9e9;
        }
        LL a, b, c, d;
        cin >> a >> b >> c >> d;
        d++;
        vector<LL> v(6);
        for (int i = 1; i <= 5; i++) {
            cin >> v[i];
        }
        LL ans = 1LL * n * v[1];
        multiset<pair<LL, LL>> se;
        for (int i = 1; i <= n; i++) {
            se.insert(make_pair(a - x[i], v[2] - v[1]));
            se.insert(make_pair(b - x[i], v[3] - v[2]));
            se.insert(make_pair(c - x[i], v[4] - v[3]));
            se.insert(make_pair(d - x[i], v[5] - v[4]));
        }
        LL res = ans;
        for (auto it : se) {
            ans += it.second;
            res = max(res, ans);
        }
        cout << res << '\n';
    }
    return 0;
}

Tokitsukaze and Sum of MxAb

根据题目公式，如果两个数都大于0，那么结果就是a[i]+a[j]，如果两个数都小于0，那么结果就是-a[i]-a[j]，如果一个数a[i]大于0一个数a[j]小于0，结果就是a[i]-a[j]，发现所有的数都会加到最终答案内，所以判断每个数被加了多少次即可，可知2n次

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        vector<int> a(n + 1);
        LL ans = 0;
        for (int i = 1; i <= n; i++) {
            cin >> a[i];
            if (a[i] < 0) {
                a[i] = -a[i];
            }
        }
        for (int i = 1; i <= n; i++) {
            ans = ans + 1LL * (2 * n) * a[i];
        }
        cout << ans << '\n';
    }
    return 0;
}

Tokitsukaze and Synthesis and Traits

根据题意可知，给出一张无向无环图，每次询问就是问有多少条不同的边，可以知道的是除了菊花图极端情况下，一般每个点所能连出去的边都是不多的，大概平均是根号左右，菊花图不优就是不优在一个点连了非常多的边，如果暴力遍历这些点所连的边会耗时非常多，那么考虑把无向图变成有向图，为了预防菊花图这种情况，可以把度小的点指向度大的点，这样即使暴力遍历，最多也就根号n个点左右，而且也不妨碍答案的统计，时间复杂度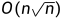

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, m, q;
    cin >> n >> m >> q;
    vector<pair<int, int>> a(m);
    vector<int> grade(n + 1);
    vector<vector<int>> G(n + 1);
    for (int i = 0; i < m; i++) {
        cin >> a[i].first >> a[i].second;
        grade[a[i].first]++;
        grade[a[i].second]++;
    }
    for (int i = 0; i < m; i++) {
        if (grade[a[i].first] < grade[a[i].second]) {
            G[a[i].first].push_back(a[i].second);
        } else {
            G[a[i].second].push_back(a[i].first);
        }
    }
    while (q--) {
        int k;
        cin >> k;
        vector<int> b(k);
        vector<bool> vis(n + 1);
        for (int i = 0; i < k; i++) {
            cin >> b[i];
            vis[b[i]] = true;
        }
        int ans = 0;
        for (int i = 0; i < k; i++) {
            for (auto v : G[b[i]]) {
                if (vis[v]) {
                    ans++;
                }
            }
        }
        cout << ans << '\n';
    }
    return 0;
}

Tokitsukaze and Three Integers

根据题意，需要计算的是(a[i]*a[j]+a[k])%p结果在0~p-1的次数，因为i,j,k都是1~n，n立方肯定凉透了，那么考虑n方log或者n方左右，那么可以提前预处理出a[i]*a[j]%p的结果在0~p-1的次数，又因为i,j,k各不相同，所以最终答案要减去(a[i]*a[j]+a[i])%p和(a[i]*a[j]+a[j])%p，这样i,j从1~n枚举常数太大，考虑减小常数，因为i,j都从1~n枚举，说明(i,j)都跑了两遍，所以每次减的时候要减2，计算+a[k]%p的时候同理

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, p;
    cin >> n >> p;
    vector<int> a(n + 1), ans(p);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        a[i] %= p;
    }
    map<int, int> mp1;
    for (int i = 1; i <= n; i++) {
        for (int j = i + 1; j <= n; j++) {
            if (i != j) {
                int x = a[i] * a[j] % p;
                mp1[x]++;
                x = (x + a[i]) % p;
                ans[x] -= 2;
                x = (x - a[i] + p) % p;
                x = (x + a[j]) % p;
                ans[x] -= 2;
            }
        }
    }
    for (auto it : mp1) {
        for (int i = 1; i <= n; i++) {
            ans[(it.first + a[i]) % p] += it.second * 2;
        }
    }
    for (int i = 0; i < p; i++) {
        cout << ans[i] << " \n"[i == p - 1];
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/171865.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

6. 基本数据类型

6. 基本数据类型

1. Python 中的变量不需要声明 每个变量在使用前都必须赋值&#xff0c;变量赋值以后该变量才会被创建。在 Python 中&#xff0c;变量就是变量&#xff0c;它没有类型&#xff0c;我们所说的"类型"是变量所指的内存中对象的类型。 counter 100 # 整型 mile…
阅读更多...
关于Win11打开文档总是提示“选择一个程序打开”的问题

关于Win11打开文档总是提示“选择一个程序打开”的问题

这边异常情况&#xff1a; 使用的360浏览器下载回来的文档、微信下载回来的文档都会出现标题所说的问题。 问题产生的原因&#xff1a; 初期在重装电脑后&#xff0c;将自带的一些安装系统后的第三方软件卸载掉了&#xff0c;也包括QQ浏览器。 可是在win11默认应用中看到了…
阅读更多...
第五章SpringFramework之AOP

第五章SpringFramework之AOP

文章目录AOP概念及相关术语概述为什要用 AOP相关术语横切关注点Advice通知Join Point连接点Point CUT 切入点切面目标代理基于注解的SpringAOP准备工作切入点表达式语法重用切入点表达式对应的切面前置通知返回通知异常通知后置通知环绕通知切面的优先级总结Spring AOP 的实现步…
阅读更多...
27.Isaac教程--局部建图

27.Isaac教程--局部建图

26.Isaac教程-局部建图 ISAAC教程合集地址: https://blog.csdn.net/kunhe0512/category_12163211.html 局部地图是机器人周围直接环境的基于网格的简化表示。 这些简化的世界表示对于安全地规划机器人附近的静态和动态障碍物至关重要。 局部建图管道将来自连接到机器人的不同传…
阅读更多...
信息服务上线渗透检测网络安全检查报告和解决方案2(安装文件信息泄漏、管理路径泄漏、XSS漏洞、弱口令、逻辑漏洞、终极上传漏洞升级)

信息服务上线渗透检测网络安全检查报告和解决方案2(安装文件信息泄漏、管理路径泄漏、XSS漏洞、弱口令、逻辑漏洞、终极上传漏洞升级)

系列文章目录 信息服务上线渗透检测网络安全检查报告和解决方案 文章目录系列文章目录前言一、XSS漏洞漏洞危害解决方案1.参数过滤2.Cookie设置HttpOnly二、安装文件目录信息泄漏漏洞证明解决方案三、后台管理路径泄漏、暴力破解、明文传输漏洞证明解决方案四、逻辑漏洞漏洞验证…
阅读更多...
LINUX学习之文件处理常用命令(三)

LINUX学习之文件处理常用命令(三)

ls 命令描述 ls命令是linux系统中用来列出文件和目录的常用命令&#xff0c;它可以显示文件和目录的名称、权限、大小、修改时间等信息 以下是ls命令的常用参数: -a &#xff1a;列出全部的文件&#xff0c;连同隐藏文件-d &#xff1a;仅列出文件目录&#xff0c;而不是列…
阅读更多...
【K哥爬虫普法】辛苦钱被中间商抽走八成，还因此锒铛入狱

【K哥爬虫普法】辛苦钱被中间商抽走八成，还因此锒铛入狱

我国目前并未出台专门针对网络爬虫技术的法律规范&#xff0c;但在司法实践中&#xff0c;相关判决已屡见不鲜&#xff0c;K 哥特设了“K哥爬虫普法”专栏&#xff0c;本栏目通过对真实案例的分析&#xff0c;旨在提高广大爬虫工程师的法律意识&#xff0c;知晓如何合法合规利用…
阅读更多...
【Python百日进阶-数据分析】Day229 - plotly的动画

【Python百日进阶-数据分析】Day229 - plotly的动画

文章目录一、动画1.1 基本动画1.2 使用 Plotly Express 制作动画条形图1.3 当前动画限制和注意事项二、为动画添加控制按钮2.1 简单的播放按钮2.2 曲线上的移动点2.3 沿平面曲线移动 Frenet 框架2.4 使用滑块和按钮三、MRI 体积切片的可视化一、动画 使用 Plotly Express 制作…
阅读更多...
23种设计模式（九）——抽象工厂模式【对象创建】

23种设计模式（九）——抽象工厂模式【对象创建】

文章目录 意图什么时候使用抽象工厂真实世界类比解决方案抽象工厂模式的实现抽象工厂模式的优缺点亦称： Abstract Factory 意图 抽象工厂是创建型设计模式，它强调了一系列相关产品对象（属于同一个产品族）的创建过程，它和工厂方法模式的侧重点不同，工厂方法模式更加侧重于…
阅读更多...
JUC面试（四）——ABA问题

JUC面试（四）——ABA问题

ABA问题 从AtomicInteger引出下面的问题 CAS -> Unsafe -> CAS底层思想 -> ABA -> 原子引用更新 -> 如何规避ABA问题 假设现在有两个线程&#xff0c;分别是T1 和 T2&#xff0c;然后T1执行某个操作的时间为10秒&#xff0c;T2执行某个时间的操作是2秒&#…
阅读更多...
Python---人生重开模拟器(简版)

Python---人生重开模拟器(简版)

专栏&#xff1a;python 个人主页&#xff1a;HaiFan. 专栏简介&#xff1a;本专栏主要更新一些python的基础知识&#xff0c;也会实现一些小游戏和通讯录&#xff0c;学时管理系统之类的&#xff0c;有兴趣的朋友可以关注一下。 人生重开模拟器思维导图前言一、设置初始属性1.…
阅读更多...
〖百宝书-思维锻炼③〗——三心理论——成功的来源

〖百宝书-思维锻炼③〗——三心理论——成功的来源

大家好&#xff0c;我是涵子&#xff0c;今天我们来聊聊三心理论。 &#x1f4ac; 人生格言&#xff1a;Stay foolish, stay kind.&#x1f4ac; &#x1f4eb; 如果文章知识点有错误的地方&#xff0c;请指正&#xff01;和大家一起学习&#xff0c;一起进步&#x1f440; &a…
阅读更多...
Ae 效果详解：CC Snowfall

Ae 效果详解：CC Snowfall

效果/模拟/CC SnowfallEffects/Simulation/CC Snowfall示例CC Snowfall &#xff08;下雪效果&#xff09;&#xff0c;可用来模拟带景深、光效和运动模糊的下雪效果。Flakes 雪花片数用于设置雪花片的数量。默认值 10000。Size 大小用于设置雪花片的大小。默认值 3.00。Variat…
阅读更多...
连续系统PID的Simulink仿真-3

连续系统PID的Simulink仿真-3

利用简化S函数&#xff0c;实现连续系统PID的Simulink仿真-2中S函数同样的功能。利用S函数简化形式实现被控对象的表达、控制器的设计及仿真结果的输出。在简化S函数中&#xff0c;flag-0时为S函数初始化&#xff0c;其中 sys包括6个参数:第1个参数表示连续系统的阶数;第2个参数…
阅读更多...
DBCO-PEG-4ARM，四臂聚乙二醇二苯基环辛炔，4Arm PEG-DBCO

DBCO-PEG-4ARM，四臂聚乙二醇二苯基环辛炔，4Arm PEG-DBCO

●中文名&#xff1a;四臂-聚乙二醇-二苯基环辛炔 ●英文名&#xff1a;4Arm PEG-DBCO&#xff0c;DBCO PEG 4ARM ●外观以及性质&#xff1a; ​4Arm PEG-DBCO产物呈固体或粘性液体&#xff0c;取决于PEG分子量&#xff0c;高分子DBCO功能化PEG&#xff0c;“点击化学"…
阅读更多...
【JavaScript】事件相关知识详解

【JavaScript】事件相关知识详解

&#x1f4bb; 【JavaScript】事件相关知识详解&#x1f3e0;专栏&#xff1a;JavaScript &#x1f440;个人主页&#xff1a;繁星学编程&#x1f341; &#x1f9d1;个人简介&#xff1a;一个不断提高自我的平凡人&#x1f680; &#x1f50a;分享方向&#xff1a;目前主攻前端…
阅读更多...
CES 2023：高通从移动互联深入布局未来智驾

CES 2023：高通从移动互联深入布局未来智驾

作为全球规模最大、影响最为广泛的国际消费电子展&#xff0c;CES曾经因为三年疫情而无奈中断&#xff0c;如今终于在2023年1月重返美国拉斯维加斯。而不管是CES 2023的3200多家参展企业&#xff0c;还是数量超过10万的现场观众&#xff0c;当他们走出位于拉斯维加斯会议中心西…
阅读更多...
02Docker镜像

02Docker镜像

Docker基础2&#xff08;镜像&#xff09; 一、Docker镜像介绍 1.1 简介 镜像是一种轻量级、可执行的独立软件包&#xff0c;它包含运行某个软件所需的所有内容&#xff0c;我们把应用程序和配置依赖打包好形成一个可交付的运行环境(包括代码、运行时需要的库、环境变量和配…
阅读更多...
《Buildozer打包实战指南》第六节 buildozer.spec配置文件中的其他参数

《Buildozer打包实战指南》第六节 buildozer.spec配置文件中的其他参数

目录 android.permissions android.features android.api android.minapi android.sdk android.ndk android.ndk_api android.private_storage android.ndk_path android.sdk_path android.ant_path android.skip_update android.accept_sdk_license android.a…
阅读更多...
【Linux】基础：线程的概念

【Linux】基础：线程的概念

【Linux】基础&#xff1a;线程的概念 摘要&#xff1a;本文介绍Linux下的线程概念&#xff0c;首先将会线程在系列教材中的定义进行抛出&#xff0c;从常规的操作系统进行理解线程的概念&#xff0c;在具体说明Linux下的进线程的管理与组织方式&#xff0c;以及由于该组织方式…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023