控制障碍函数CBF详解（附带案例实现）

1. Control Affine System

一个控制仿射系统的典型形式是

$$\dot{x}=F(x,u)$$

其中，$x\in {\mathbb{R}}^n$是系统的状态，$u\in {\mathbb{R}}^m$是系统的控制输入，$F$是Lipschitz连续的，这样就能保证给定一个初始状态$x(t_0)=x_0$的时候，动态系统的轨迹$x(t)$存在且唯一。

我们通常处理的是非线性系统，那么我们可以将非线性的仿射系统写成如下的形式

$$\dot{x}=f(x)+g(x)u$$

其中$f:{\mathbb{R}}^n\to {\mathbb{R}}^n$是系统的漂移向量场，它描述了系统在没有控制输入时的动态行为，$g:{\mathbb{R}}^n\to {\mathbb{R}}^{n\times m}$，是系统的控制向量场，它描述了系统的控制输入$u$是如何影响系统的。

2. Lyapunov Theory, Nagumo’s Theory, Invariance Principle

Lyapunov Theory

对于系统$\dot{x}=f(x)$而言，$x\in {\mathbb{R}}^n$是系统的状态，$f:{\mathbb{R}}^n\to {\mathbb{R}}^n$是一个系统状态的映射函数。如果

$$\begin{gathered} \exists V(x) \\ \text{s.t. }V(x_e)=0,V(x)>0\text{ for }x\ne x_e, \\ \dot{V}(x)=\frac{\partial V}{\partial x}f(x)<0\text{ for }x\ne x_e \end{gathered}$$

那么系统则是稳定的。并且状态$x$所构成的集合，可以被称为是一个不变集（Invariance set）。

不变集合： 集合$\mathcal{C}$被称为不变的，如果系统从$\mathcal{C}$内的任意一点开始演化，那么系统的轨迹始终停留在$\mathcal{C}$内。

Nagumo’s Theory

对于系统$\dot{x}=f(x)$而言，$x\in {\mathbb{R}}^n$是系统的状态， C = { x ∣ h ( x ) ≥ 0 } \mathcal{C}=\{x|h(x)\ge0\} C={x∣h(x)≥0}是映射$h:{\mathbb{R}}^n\to \mathbb{R}$的一个上水平集，如果

$$\begin{gathered} \dot{h}(x)\ge 0 \\ \forall x\in \partial \mathcal{C} \end{gathered}$$

那么$\mathcal{C}$是一个不变集。符号的具体含义如下：

C = { x ∈ D ⊂ R n : h ( x ) ≥ 0 } , ∂ C = { x ∈ D ⊂ R n : h ( x ) = 0 } , Int ( C ) = { x ∈ D ⊂ R n : h ( x ) > 0 } , \begin{align*} \mathcal{C} & = \{ x\in D\sub \mathbb{R}^n: h(x) \ge 0 \}, \\ \partial\mathcal{C} & = \{ x\in D\sub \mathbb{R}^n: h(x) = 0 \}, \\ \text{Int}(\mathcal{C}) & = \{ x\in D\sub \mathbb{R}^n: h(x) > 0 \}, \end{align*} C∂CInt(C)​={x∈D⊂Rn:h(x)≥0},={x∈D⊂Rn:h(x)=0},={x∈D⊂Rn:h(x)>0},​

集合$\mathcal{C}$是安全集，$\partial \mathcal{C}$是安全集的边界，$\text{Int}(\mathcal{C})$是安全集的内部点。

3. Control Lyapunov Function (CLF) and CLF-QP

Control Lyapunov Function

设$V(x):{\mathbb{R}}^n\to \mathbb{R}$是一个连续可微的函数，如果这里存在一个常量$c>0$使得

1)  Ω c : = { x ∈ R n : V ( x ) ≤ c } ,  a sublevel set of  V ( x )  is bounded 2)  V ( x ) > 0 , ∀ s ∈ R n \ { x e } , V ( x e ) = 0 3)  inf ⁡ u ∈ U V ˙ ( x , u ) < 0 , ∀ x ∈ Ω c \ { x e } \begin{align*} & \text{1) }\Omega_c := \{ x\in\mathbb{R}^n: V(x) \le c\}, \text{ a sublevel set of } V(x) \text{ is bounded} \\ & \text{2) }V(x) > 0, \forall s \in\mathbb{R}^n \backslash \{x_e\}, V(x_e) = 0 \\ & \text{3) }\inf_{u\in U} \dot{V}(x,u) < 0, \forall x \in \Omega_c \backslash \{x_e\} \end{align*} ​1) Ωc​:={x∈Rn:V(x)≤c}, a sublevel set of V(x) is bounded2) V(x)>0,∀s∈Rn\{xe​},V(xe​)=03) u∈Uinf​V˙(x,u)<0,∀x∈Ωc​\{xe​}​

1）存在一个子集，使得$V(x)\le c$是有界的

2）Lyapunov函数不在原点时大于零，在原点时等于零

3）对于控制量和系统状态来说，总使得$V(x)$的导数$\dot{V}(x)$小于零。

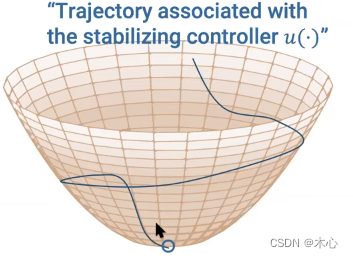
其中，$V(x)$可以被称为局部控制李雅普诺夫函数，${\Omega }_c$是一个引力区（Region of Attraction, ROA），${\Omega }_c$中的每一个点都会收敛到$x_e$，整个轨迹就如下图所示，会一直保持在这个区域内，并且最终收敛到$x_e$，这其实就是一种渐进稳定。

我们可以将导数显示地写出来

$$\begin{array}{rl}\dot{V}(x)& =\nabla V(x)\dot{x}\\ & =\nabla V(x)f(x)+\nabla V(x)g(x)u\\ & =L_{f}V(x)+L_{g}V(x)u\end{array}$$

其中$L_{p}q(x)=\nabla q(x)\cdot p(x)$是李导数算子，使得公式更加简洁。

为了使收敛更加迅速，我们需要考虑收敛的时间限制，指数收敛是一种快速的方式，所以我们希望最终的结果能够按照指数的方式进行收敛。

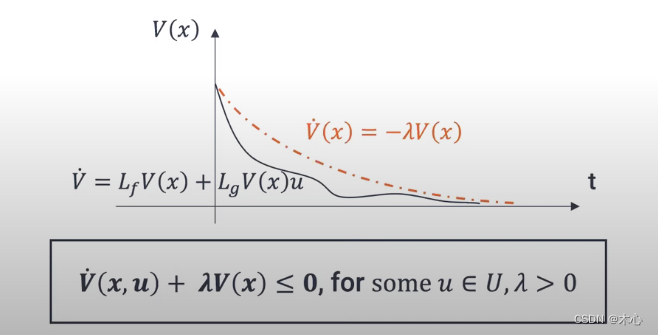
我们可以增加一个判断条件，设$V(x):{\mathbb{R}}^n\to \mathbb{R}$是连续可微、正定、有界的函数，如果$\exists \lambda >0$使得

$$\text{4) }\underset{u\in U}{\inf }\dot{V}(x,u)+\lambda V(x)\le 0$$

或者写成

$$\underset{u\in U}{\inf }[L_{f}V(x)+L_{g}V(x)u]+\lambda V(x)\le 0$$

那么$V(x)$就是指数稳定的控制李雅普诺夫函数（exponentially stabilizing CLF，ES-CLF），其中$\lambda$是$V(x(t))$上界的衰减率。

Control Lyapunov Function Quadratic Program

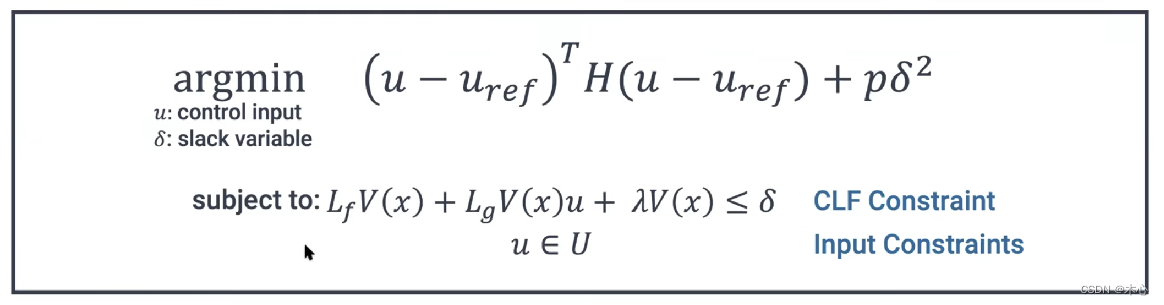
CLF约束对于$u$是线性的，因此用最小范数控制器，二次规划的目标位最小化控制量，受限制为，满足李雅普诺夫函数收敛的上界以及控制量 $u$在解集内。由于这个优化为一个凸优化问题，因此其实时性是可以被保证的，CLF约束通常用松弛变量来保证问题的可行性，如果没有松弛变量，控制器将指数稳定到系统原点$x_e$

4. Control Barrier Function (CBF) and CBF-CLF-QP

设$B(x):{\mathbb{R}}^n\to \mathbb{R}$是连续、可微的函数， C = { x ∣ B ( x ) ≥ 0 } \mathcal{C}=\{x|B(x)\ge 0\} C={x∣B(x)≥0}是该函数的零上水平集，并且$\nabla B(x)\ne 0,\forall x\in \partial \mathcal{C}$，如果$\exists \gamma$使得$\forall x\in \mathcal{C}$

$$\underset{u\in U}{\sup }[L_{f}B(x)+L_{g}B(x)u]+\gamma B(x)\ge 0$$

那么$B(x)$就被称作Control Barrier Function

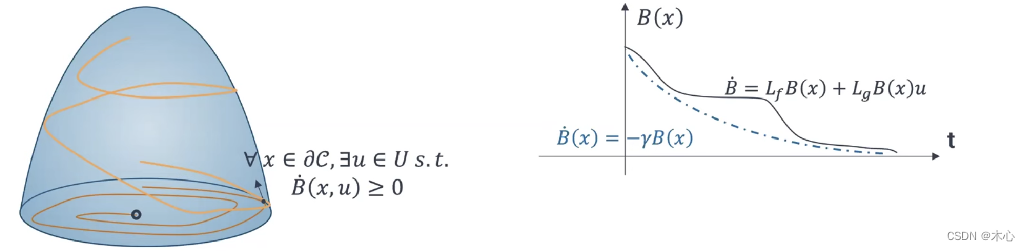
因此这个二次规划问题就变成了

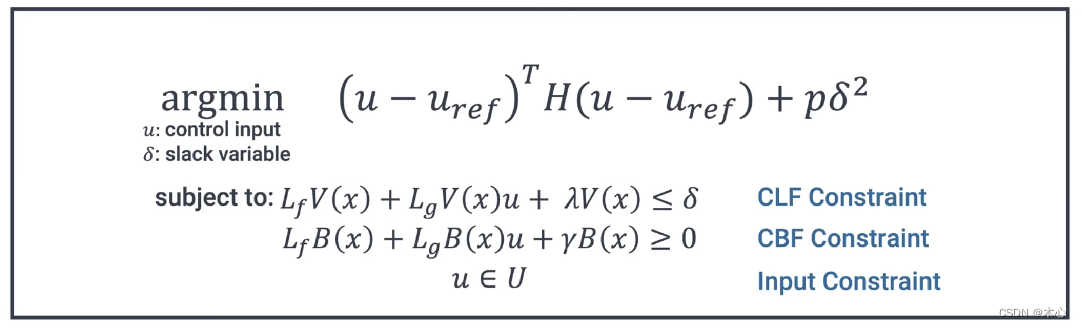
5. A Toy Example

我们考虑一个简单的例子，在这个例子中有两辆车辆，分别是lead vehicle和ego vehicle，如下图所示

下面我们先推导一下，然后再进行仿真验证。

5.1 Derivation

设计我们的状态量为：$x=[p,v,z{]}^T\in {\mathbb{R}}^3$，系统的微分方程为：

$$\{\begin{array}{rl}\dot{p}& =v\\ \dot{v}& =\frac{u-F_r(v)}{m},F_r(v)=f_0+f_{1}v+f_2{v}^2\\ \dot{z}& =v_0-v\end{array}$$

其中F_r(v)是摩擦力，将微分方程写成矩阵的形式

$$\dot{x}=\left[\begin{array}{c}\dot{p}\\ \dot{v}\\ \dot{z}\end{array}\right]=\left[\begin{array}{c}v\\ -\frac{1}{m}{F}_r(v)\\ v_0-v\end{array}\right]+\left[\begin{array}{c}0\\ \frac{1}{m}\\ 0\end{array}\right]u$$

为了保障系统的安全性，给系统的输入做如下的限制

$$-m{c}_{d}g\le u\le m{c}_{a}g$$

ego vehicle的目标速度为

$$v\to v_d$$

最小安全距离必须满足时间前瞻量的限制$T_h$

$$z\ge T_{h}v$$

系统的平衡点$x_e=[\cdot ,v_d,\cdot {]}^T$设计Lyapunov Function $V(x)$

$$\begin{array}{rl}V(x)& =(v-v_d{)}^2\\ \dot{V}(x)& =\nabla V(x)\dot{x}\end{array}$$

其中

$$\begin{gathered} \nabla V(x)=[0,2(v-v_d),0] \\ \dot{x}=\left[\begin{array}{c}v\\ -\frac{1}{m}{F}_r(v)\\ v_0-v\end{array}\right]+\left[\begin{array}{c}0\\ \frac{1}{m}\\ 0\end{array}\right]u \end{gathered}$$

然后我们可以获得

$$\begin{gathered} L_{f}V(x)=-\frac{2}{m}{F}_r(v)(v-v_d) \\ {L}_{g}V(x)=\frac{2}{m}(v-v_d) \end{gathered}$$

所以CLF的约束${\inf }_{u\in U}[L_{f}V(x)+L_{g}V(x)u]+\lambda V(x)\le 0$可以表示为

$$\underset{u\in U}{\inf }(v-v_d)[\frac{2}{m}(u-F_r)+\lambda (v-v_d)]\le 0$$

保障安全性的目标是$z\ge T_{h}V$，则设计CBF

$$B(x)=z-T_{h}V$$

则有

$$\begin{gathered} \nabla B(x)=[0,-T_h,1] \\ {L}_{f}B(x)=\frac{T_h}{m}{F}_r+(v_0-v),L_{g}B(x)=-\frac{T_h}{m} \end{gathered}$$

所以CBF的约束${\sup }_{u\in U}[L_{f}B(x)+L_{g}B(x)u]+\gamma B(x)\ge 0$ 可以表示为

$$\frac{T_h}{m}(F_r-u)+(v_0-v)+\gamma (z-T_{h}v)\ge 0$$

忽略$F_r$，当$u=-m{c}_{d}g$的时候，CBF的约束可以表示为

$$T_h{c}_{d}g+v_0+\gamma z-(1+T_h\gamma )v$$

当$v$足够大的时候，可能会导致CBF的约束小于0，所以我们需要重新设计CBF

$$B(x)=z-T_{h}v-\frac{1}{2}\frac{(v-v_0{)}^2}{c_{d}g}$$

则有

$$\dot{B}(x,u)=\frac{1}{m}(T_h+\frac{v-v_0}{c_{d}g})(F_r(v)-u)+(v_0-v)$$

当$u=-m{c}_{d}g$的时候，$\dot{B}(x,u)=\frac{1}{m}{T}_h{F}_r+T_h{c}_{d}g>0$，所以此CBF是一个可行的CBF，那么我们最终获得的CLF-CBF-QP为

$$\begin{array}{rl}\arg \min & u^{T}Hu\\ \text{s.t.}& (v-v_d)[\frac{2}{m}(u-F_r)+\lambda (v-v_d)]\le 0\\ & \frac{1}{m}(T_h+\frac{(v-v_0)}{c_{d}g})(F_r-u)+(v_0-v)+\gamma (z-T_{h}v)\ge 0\\ & -m{c}_{d}g\le u\le m{c}_{a}g\end{array}$$

5.2 Simulation

使用python来编写脚本代码，使用cvxopt凸优化的库来进行求解，具体可以参考cvxopt的wiki官网。

import numpy as np
import matplotlib.pyplot as plt
from cvxopt import matrix, solvers

# Simulation parameters
dt = 0.02
T = 30
length = int(np.ceil(T / dt))

# System initialization
p = np.zeros((length + 1, 1))
v = np.zeros((length + 1, 1))
z = np.zeros((length + 1, 1))
u = np.zeros((length, 1))

sys = {
    'm': 1650,
    'g': 9.81,
    'v0': 14,
    'vd': 24,
    'f0': 0.1,
    'f1': 5,
    'f2': 0.25,
    'ca': 0.3,
    'cd': 0.3,
    'T': 1.8,
    'clf_rate': 5,
    'cbf_rate': 5,
    'weight_input': 2 / 1650**2,
    'weight_slack': 2e-2
}

sys['u_max'] = sys['ca'] * sys['m'] * sys['g']
sys['u_min'] = -sys['cd'] * sys['m'] * sys['g']

# Initial conditions
p[0] = 0
v[0] = 10
z[0] = 100

# Simulation loop
for i in range(length):
    current_p = p[i, 0]
    current_v = v[i, 0]
    current_z = z[i, 0]
    x = np.array([current_p, current_v, current_z])
    
    F_r = sys['f0'] + sys['f1'] * current_v + sys['f2'] * current_v**2
    f = np.array([current_v, -F_r / sys['m'], sys['v0'] - current_v])
    g = np.array([0, 1 / sys['m'], 0])

    V = (current_v - sys['vd'])**2
    dV = np.array([0, 2 * (current_v - sys['vd']), 0])
    LfV = np.dot(dV, f)
    LgV = np.dot(dV, g)
    B = current_z - sys['T'] * current_v - 0.5 * (current_v - sys['v0'])**2 / (sys['cd'] * sys['g'])
    dB = np.array([0, -sys['T'] - (current_v - sys['v0']) / (sys['cd'] * sys['g']), 0])
    LfB = np.dot(dB, f)
    LgB = np.dot(dB, g)

    # Quadratic program
    H_ = np.array([[sys['weight_input'], 0],
                   [0, sys['weight_slack']]])
    f_ = np.array([-sys['weight_input'] * F_r, 0])
    
    A_ = np.array([[LgV, -1], 
                   [-LgB, 0],
                   [1, 0],
                   [-1, 0]])
    b_ = np.array([-LfV - sys['clf_rate'] * V, 
                   LfB + sys['cbf_rate'] * B,
                   sys['u_max'],
                   -sys['u_min']])
    
    # Convert to cvxopt format
    P = matrix(H_)
    q = matrix(f_)
    G = matrix(A_)
    h = matrix(b_)

    # Solve QP problem using cvxopt
    sol = solvers.qp(P, q, G, h)
    u_opt = sol['x'][0] # Second term is the slack variable

    dx = f + g * u_opt
    x_n = x + dx * dt

    # Save data
    u[i, 0] = u_opt
    if i < length:
        p[i + 1, 0] = x_n[0]
        v[i + 1, 0] = x_n[1]
        z[i + 1, 0] = x_n[2]

# Plotting
time = np.arange(0, T + dt, dt)

plt.figure(figsize=(10, 8))
plt.subplot(4, 1, 1)
plt.plot(time, p)
plt.ylabel('p')

plt.subplot(4, 1, 2)
plt.plot(time, v)
plt.ylabel('v')

plt.subplot(4, 1, 3)
plt.plot(time, z)
plt.ylabel('z')

plt.subplot(4, 1, 4)
plt.plot(time[:-1], u)
plt.ylabel('u')

plt.xlabel('Time (s)')
plt.tight_layout()
plt.show()

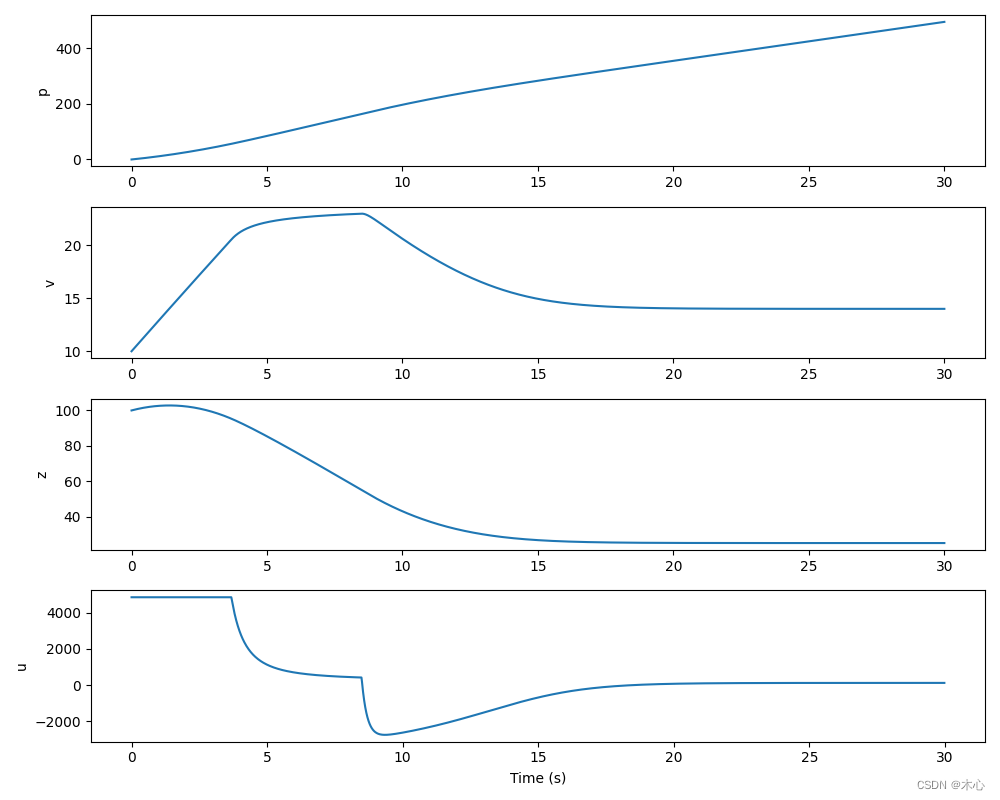
最后的结果如下

Reference

[1]Jason Choi – Introduction to Control Lyapunov Functions and Control Barrier Functions
[2]CBF-CLF-Helper