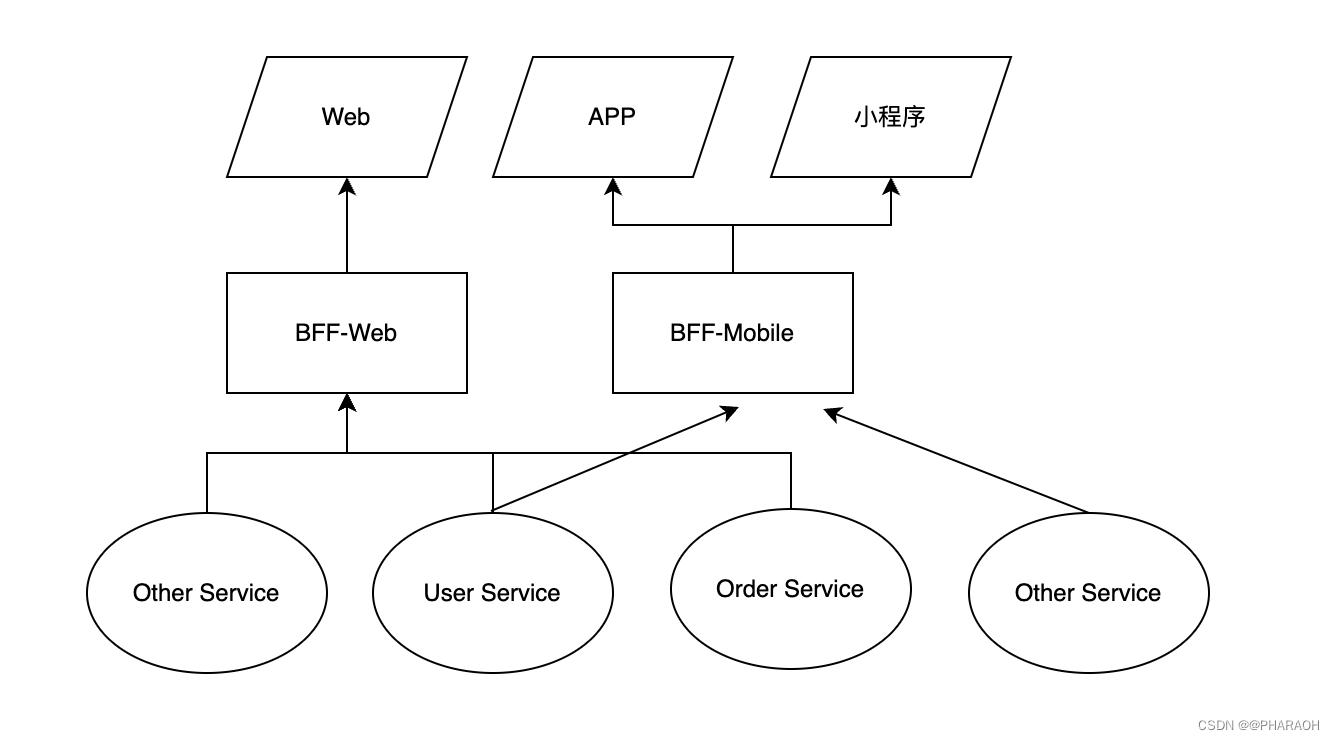
文章目录
- 算法简介
- 坏字符规则
- 坏字符的定义
- 坏字符的移动
- 好后缀规则
- 好后缀的定义
- 好后缀的移动
- 算法实现
算法简介
- BM算法也就是Boyer Moore算法,它是一种非常高效的字符串匹配算法,是一种滑动算法。
- 什么是滑动?
下面例子中,主串中的c,在模式串中不存在,所以模式串可以往后华滑动,因为只要有c存在,那么该字串肯定与模式串不匹配。
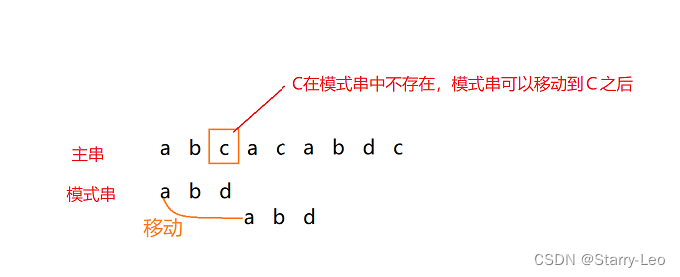
- BM算法,本质上其实就是在寻找这种规律,借助这种规律可以高效的实现字符串匹配。为了实现正确的滑动,BM算法包含了两个部分,分别是坏字符规则(bad character rule)和好后缀规则(good suffix shift)
坏字符规则
坏字符的定义
BM算法的匹配顺序是按照模式串的下标从大到小的顺序进行匹配的,当模式串的末尾倒着匹配中,发现某个字符没法匹配,我们就叫主串中的这个字符是坏字符。
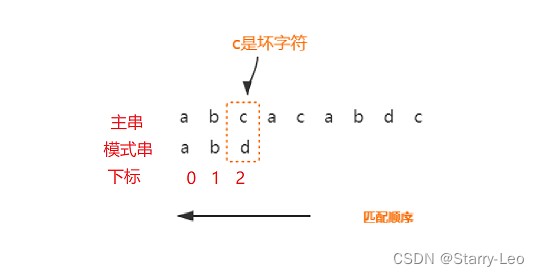
坏字符的移动
当模式串和主串的某个字串发生不匹配时,我们把坏字符串对应模式串的那个字符下标记作si,如果坏字符串在模式串中存在,我们把这个坏字符串在模式串中的下标记作xi,如果不在模式串中存在,则xi = -1。那么此时,模式串往后移动的位数就等于si - xi 。

好后缀规则
好后缀的定义
在模式串和主串字串匹配过程中,匹配上的字符串我们叫做好后缀。
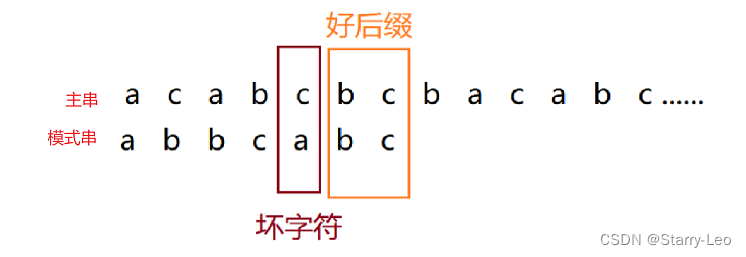
好后缀的移动
- 我们把已经匹配的子串,在模式串中查找,如果找到另外一个跟好后缀匹配的模式串子串{u},此时,移动位数=好后缀在模式串中的当前位置 - 好后缀在模式串上一次出现的位置(模式串倒数第二个好后缀),如果好后缀只在模式串中出现一次,则上一次出现位置的值为-1.
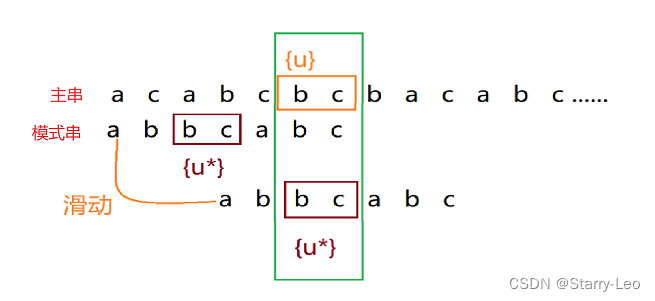
- 如果在模式串中找不到另外一个等于好后缀的字串,那么我们就直接将模式串,滑动到主串好后缀的后面。

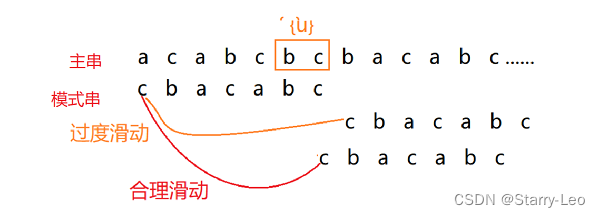
- 过度滑动的情况:当模式串滑动到前缀与主串中{u}的后缀有部分重合的时候,并且重合的部分相等的时候,就有可能会存在完全匹配的情况。针对这种情况,我们不仅要看好后缀在模式串中,是否有另一个匹配的子串,我们还要考察好后缀的后缀子串(c),是否存在跟模式串的前缀子串(c)匹配的。
算法实现
package com.xxliao.algorithms.string_match.bm;
import java.util.Arrays;
/**
* @author xxliao
* @description: 字符串匹配 BM算法
* @date 2024/5/31 16:19
*/
public class BMMatch {
public static void main(String[] args) {
String main = "acabcbcbacabc";
String pattern = "cbacabc";
System.out.println(indexOf(main,pattern));
}
private static final int CHARACTER_SIZE = 256; // 英文字符的种类,2^8
/**
* @description BM算法匹配字符串,匹配成功返回P在S中的首字符下标,匹配失败返回-1
* @author xxliao
* @date 2024/5/31 16:20
*/
public static int indexOf(String main, String pattern) {
char[] main_array = main.toCharArray();
char[] pattern_array = pattern.toCharArray();
int main_length = main_array.length;
int pattern_length = pattern_array.length;
// 模式串为空字符串,返回0
if (pattern_length == 0) {
return 0;
}
// 主串长度小于模式串长度,返回-1
if (main_length < pattern_length) {
return -1;
}
int[] bad_char_array = buildBadCharacter(pattern_array);
int[] good_char_array = buildGoodSuffix(pattern_array);
// 从尾部开始匹配,其中i指向主串,j指向模式串
for (int i = pattern_length - 1; i < main_length; ) {
int j = pattern_length - 1;
for (; main_array[i] == pattern_array[j]; i--, j--) {
if (j == 0) { // 匹配成功返回首字符下标
return i;
}
}
// 每次后移“坏字符规则”和“好后缀规则”两者的较大值
// 注意此时i(坏字符)已经向前移动,所以并非真正意义上的规则
i += Math.max(bad_char_array[main_array[i]], good_char_array[pattern_length - 1 - j]);
}
return -1;
}
/**
* @description 坏字符规则表,数组内默认填充的是后移位数
* @author xxliao
* @date 2024/5/31 16:30
*/
private static int[] buildBadCharacter(char[] pattern) {
int pattern_length = pattern.length;
int[] bad_char_array = new int[CHARACTER_SIZE]; // 记录坏字符出现时后移位数
Arrays.fill(bad_char_array, pattern_length); // 默认后移整个模式串长度
for (int i = 0; i < pattern_length - 1; i++) {
int ascii = pattern[i]; // 当前字符对应的ASCII值
bad_char_array[ascii] = pattern_length - 1 - i; // 对应的后移位数,若重复则以最右边为准
}
return bad_char_array;
}
/**
* @description 非真正意义上的好字符规则表,后移位数还加上了当前好后缀的最大长度
* @author xxliao
* @date 2024/5/31 16:30
*/
private static int[] buildGoodSuffix(char[] pattern) {
int pattern_length = pattern.length;
int[] good_char_array = new int[pattern_length]; // 记录好后缀出现时后移位数
int last_prefix_pos = pattern_length; // 好后缀的首字符位置
for (int i = pattern_length - 1; i >= 0; i--) {
// 判断当前位置(不含)之后是否是好后缀,空字符也是好后缀
if (isPrefix(pattern, i + 1)) {
last_prefix_pos = i + 1;
}
// 如果是好后缀,则GS=pLen,否则依次为pLen+1、pLen+2、...
good_char_array[pattern_length - 1 - i] = last_prefix_pos - i + pattern_length - 1;
}
// 上面在比较好后缀时,是从模式串的首字符开始的,但实际上好后缀可能出现在模式串中间。
// 比如模式串EXAMPXA,假设主串指针在比较P时发现是坏字符,那么XA就是好后缀,
// 虽然它的首字符X与模式串的首字符E并不相等。此时suffixLen=2表示将主串指针后移至模式串末尾,
// pLen-1-i=4表示真正的好字符规则,同样主串指针后移,使得模式串前面的XA对齐主串的XA
for (int i = 0; i < pattern_length - 1; i++) {
int suffixLen = suffixLength(pattern, i);
good_char_array[suffixLen] = pattern_length - 1 - i + suffixLen;
}
return good_char_array;
}
/**
* @description 判断是否是好后缀,即模式串begin(含)之后的子串是否匹配模式串的前缀
* @author xxliao
* @date 2024/5/31 16:30
*/
private static boolean isPrefix(char[] pattern, int begin) {
for (int i = begin, j = 0; i < pattern.length; i++, j++) {
if (pattern[i] != pattern[j]) {
return false;
}
}
return true;
}
/**
* @description 返回模式串中以pattern[begin](含)结尾的后缀子串的最大长度
* @author xxliao
* @date 2024/5/31 16:30
*/
private static int suffixLength(char[] pattern, int begin) {
int suffixLen = 0;
int i = begin;
int j = pattern.length - 1;
while (i >= 0 && pattern[i] == pattern[j]) {
suffixLen++;
i--;
j--;
}
return suffixLen;
}
}