前言:海明编码这一块在刚开始的时候没有弄懂,后面通过做实验、复习慢慢摸清了门道。在学习计算机组成原理的过程中,实验实践是很重要的,它会让你去搞清楚事情背后的原理,逼着你学会你没听懂的东西。这篇文章会从海明码的理论部分和实验部分进行阐述。
海明码
奇偶校验码
为什么要谈到奇偶校验码呢?因为它和海明码一样,都属于校验码。所谓校验码,就是数据位和校验位的合并,通过校验位的信息,你能知道数据是不是出错了,哪里出错了,它本应是多少。

注:后文均用 k k k 表示原式数据位数, r r r 表示校验位位数(也同时是校验组的组数), n n n 表示校验码(数据位 + 校验位)的总位数。
正如上图所示,校验码主要是用于数据发送方和接收方通信用的,通过校验位可以检查传过来的数据是否准确。
偶校验码通过设置
r
=
1
r=1
r=1 位校验位
P
P
P,使得校验码
P
D
k
⋯
D
2
D
1
PD_k\cdots D_2D_1
PDk⋯D2D1 所有位共有偶数个
1
1
1。计算公式是
P
=
D
1
⊕
D
2
⊕
⋯
⊕
D
k
(1)
P=D_1\oplus D_2\oplus\cdots\oplus D_k\tag 1
P=D1⊕D2⊕⋯⊕Dk(1)
比如发送方需要传输
k
=
5
k=5
k=5 位数据
11001
11001
11001,会生成一位校验位
1
1
1,打包成校验码
1
11001
\red{1}11001
111001 送给接收方。如果传输过程没有发生错误,接收方收到的就是
111001
111001
111001,看一下有
1
1
1 的个数是偶数,应该是没问题。如果传输过程中有一位出错了,比如
111001
→
11
0
001
111001\rightarrow 11\red 0001
111001→110001,接收方收到的数据就有奇数个
1
1
1,所以就能够判断传过来的数据出错了(但是不能分辨是哪一位错了)。
奇偶校验码的缺点也是显而易见的,对偶校验码来说,如果传输过程中出现了
2
2
2 位错误,接收方就会认为是正确的,这说明奇偶校验码最多检错
1
1
1 位。
码距
定长编码中任意两个合法编码最少有多少位不同,这个编码的码距就是多少。比如上面的奇偶校验码码距就是 2 2 2。海明码的码距是 3 3 3。
海明码
有多种类型的海明码校验,这里只介绍能纠一位错的海明码。
多校验组
前面提到,奇偶校验码可以检测
1
1
1 位错,但是不具备纠错能力。并且所有数据位于
1
1
1 个校验组中,即
r
=
1
r=1
r=1。
海明码在
k
k
k 位数据位中插入
r
r
r 个校验位,使得每个数据至少位于
2
2
2 个校验组中(为什么?后面会解释)。也就意味着对于某个
D
s
D_s
Ds 而言,它至少要参与
P
i
P_i
Pi 和
P
j
(
i
≠
j
)
P_j(i\neq j)
Pj(i=j) 的生成。同样的,
P
i
P_i
Pi 是由某一些数据位异或得到的,
P
i
P_i
Pi 和这些数据位共同构成
1
1
1 个校验组(偶校验组)。
P
i
=
D
i
1
⊕
D
i
2
⊕
⋯
⊕
D
i
t
(2)
P_i=D_{i1}\oplus D_{i2}\oplus \cdots\oplus D_{it}\tag 2
Pi=Di1⊕Di2⊕⋯⊕Dit(2)
式 ( 2 ) (2) (2) 描述了第二个第 i i i 个校验位的生成。
省流:每个校验组都是由一个 P P P 和若干 D D D 构成的, P P P 是这些 D D D 的异或结果。
接收方会生成一种叫检错码的东西,每个校验位生成
1
1
1 个检错码,所以一共有
r
r
r 个检错码,用
G
i
(
i
=
1
,
2
,
⋯
,
r
)
G_{i}(i=1,2,\cdots,r)
Gi(i=1,2,⋯,r) 来表示。 接收方会干这样的事情:
G
i
=
P
i
′
⊕
D
i
1
′
⊕
D
i
2
′
⊕
⋯
⊕
D
i
t
′
(3)
G_i=P_i'\oplus D_{i1}'\oplus D_{i2}'\oplus\cdots\oplus D_{it}'\tag 3
Gi=Pi′⊕Di1′⊕Di2′⊕⋯⊕Dit′(3)
其中加一个 ′ ' ′ 表示数据传输后的结果,比如发送方的 D 4 D_4 D4 在接收方变成了 D 4 ′ D_4' D4′。
注意 G i G_i Gi(检错码) 和 P i P_i Pi (校验码)是不同的东西, P i P_i Pi 是发送方根据 D D D 生成的; G i G_i Gi 是接收方根据 P i ′ P_i' Pi′ 和 D ′ D' D′ 生成的,用于检错。海明码的实现中结合了偶校验的思想。
显然,如果接收方发现 G i = 1 G_i=1 Gi=1,就说明第 i i i 个校验组有数据出错了。但是到底是谁出错了?是 P i P_i Pi 还是对应的 D i t D_{it} Dit 呢?
海明码原理
海明码致力于制定一套规则回答上面的问题。它将
k
k
k 个数据位
D
D
D 和
r
r
r 个校验位
P
P
P 以某种方式组合成
n
n
n 位校验码
H
H
H,以某种方式划分校验组,以期达到这样的目标:
G
r
⋯
G
1
G_r\cdots G_1
Gr⋯G1 直接指示出错的位置。比如
G
3
G
2
G
1
=
011
G_3G_2G_1=011
G3G2G1=011,代表海明码的
H
3
H_3
H3 出错了。其中,预留
G
3
G
2
G
1
=
000
G_3G_2G_1=000
G3G2G1=000 代表没有错误。
因此,对于海明码
n
=
k
+
r
n=k+r
n=k+r 位来说,
1
1
1 位错一共有
k
+
r
k+r
k+r 种可能,但是
G
r
⋯
G
1
G_r\cdots G_1
Gr⋯G1 只能指示
2
r
−
1
2^r-1
2r−1 种错误。所以应该有:
k
+
r
≤
2
r
−
1
(4)
k+r\leq 2^r-1\tag4
k+r≤2r−1(4)
并且,由于海明码要实现纠错功能,码距就不能是 2 2 2,至少要是 3 3 3,否则就会像奇偶校验码一样只能检错、不能纠错。为了减少冗余,海明码的码距设定为 3 3 3。这就意味着每个数据位 D s D_s Ds 至少要出现在 2 2 2 个校验组中。
假设数据位 D s D_s Ds 只出现在校验组 P i P_i Pi 中。当 D s = 0 D_s=0 Ds=0 时,记 P i = k P_i=k Pi=k,得到的海明码是 H \boldsymbol H H;当 D s = 1 D_s=1 Ds=1 时,根据异或的性质,有 P i = k ‾ P_i=\overline k Pi=k,得到的海明码是 H ′ \boldsymbol {H'} H′。你会发现 H \boldsymbol H H 和 H ′ \boldsymbol{H'} H′ 只有 D s D_s Ds 和 P i P_i Pi 两位是不一样的,那么海明码的码距就是 2 2 2。但是我们海明码的码距是 3 3 3,所以 D s D_s Ds 只出现在一个校验组是不够的。
现在我们来看海明码是怎么编码的。假设
r
=
3
r=3
r=3 的海明码,检错位是
G
3
G
2
G
1
=
001
G_3G_2G_1=001
G3G2G1=001——这说明只有校验组
1
1
1 出错了。那可能是生成
P
1
P_1
P1 的那些
D
D
D 出错了吗?不可能,因为一旦
D
D
D 出错,
G
3
G
2
G
1
G_3G_2G_1
G3G2G1 就至少有两个
1
1
1(至少两个校验组出错)了,因为每个数据位都至少要出现在
2
2
2 个校验组中。
所以,对于
G
3
G
2
G
1
G_3G_2G_1
G3G2G1 只有一位
1
1
1 的情况,只能是校验组所对应的检错位出错了。
那么
G
3
G
2
G
1
=
001
/
010
/
100
G_3G_2G_1=001/010/100
G3G2G1=001/010/100 分别对应检错位
P
1
,
P
2
,
P
3
P_1,P_2,P_3
P1,P2,P3 出错,根据海明码的目标“
G
r
⋯
G
1
G_r\cdots G_1
Gr⋯G1 直接指示出错的位置”,应该把
P
1
P_1
P1 放在
H
1
H_1
H1,
P
2
P_2
P2 放在
H
2
H_2
H2,
P
3
P_3
P3 放在
H
4
H_4
H4。且看下面的表格:
| 海明码 | H 1 H_1 H1 | H 2 H_2 H2 | H 3 H_3 H3 | H 4 H_4 H4 | H 5 H_5 H5 | H 6 H_6 H6 | H 7 H_7 H7 |
|---|---|---|---|---|---|---|---|
| 检错码/位置 G 3 G 2 G 1 G_3G_2G_1 G3G2G1 | 001 001 001 | 010 010 010 | 011 011 011 | 100 100 100 | 101 101 101 | 110 110 110 | 111 111 111 |
| 映射关系 (这一位 H H H 放什么) | P 1 P_1 P1 | P 2 P_2 P2 | D 1 D_1 D1 | P 3 P_3 P3 | D 2 D_2 D2 | D 3 D_3 D3 | D 4 D_4 D4 |
| 属于 G 1 G_1 G1 校验组 | √ | √ | √ | √ | |||
| 属于 G 2 G_2 G2 校验组 | √ | √ | √ | √ | |||
| 属于 G 3 G_3 G3 校验组 | √ | √ | √ | √ |
这个表格是对应海明码在
(
n
,
k
)
=
(
7
,
4
)
(n,k)=(7,4)
(n,k)=(7,4) 时的分组规则。预留了
G
3
G
2
G
1
=
000
G_3G_2G_1=000
G3G2G1=000 ,对应海明码没有出错。其实上面
D
D
D 的位置是可以随便放的,这个只影响后面校验位
P
P
P 的生成表达式。按照上面的
D
D
D 的放置方式,有:
{
P
1
=
D
1
⊕
D
2
⊕
D
4
P
2
=
D
1
⊕
D
3
⊕
D
4
P
3
=
D
2
⊕
D
3
⊕
D
4
(5)
\begin{cases}P_1=D_1\oplus D_2\oplus D_4\\P_2=D_1\oplus D_3\oplus D_4\\P_3=D_2\oplus D_3\oplus D_4\end{cases}\tag 5
⎩
⎨
⎧P1=D1⊕D2⊕D4P2=D1⊕D3⊕D4P3=D2⊕D3⊕D4(5)
式
(
5
)
(5)
(5) 是发送方要干的事情。给发送方一个
D
4
D
3
D
2
D
1
D_4D_3D_2D_1
D4D3D2D1,发送方需要按照
(
5
)
(5)
(5) 生成
P
3
P
2
P
1
P_3P_2P_1
P3P2P1,然后打包成
H
7
H
6
H
5
H
4
H
3
H
2
H
1
=
D
4
D
3
D
2
P
3
D
1
P
2
P
1
H_7H_6H_5H_4H_3H_2H_1=D_4D_3D_2P_3D_1P_2P_1
H7H6H5H4H3H2H1=D4D3D2P3D1P2P1,发送给接收方。
根据式
(
2
)
(
3
)
(2)(3)
(2)(3),接收方需要按照下面的方式生成检错位:
{
G
1
=
P
1
′
⊕
D
1
′
⊕
D
2
′
⊕
D
4
′
G
2
=
P
2
′
⊕
D
1
′
⊕
D
3
′
⊕
D
4
′
G
3
=
P
3
′
⊕
D
2
′
⊕
D
3
′
⊕
D
4
′
(6)
\begin{cases}G_1=P_1'\oplus D_1'\oplus D_2'\oplus D_4'\\ G_2=P_2'\oplus D_1'\oplus D_3'\oplus D_4'\\ G_3=P_3'\oplus D_2'\oplus D_3'\oplus D_4'\end{cases}\tag 6
⎩
⎨
⎧G1=P1′⊕D1′⊕D2′⊕D4′G2=P2′⊕D1′⊕D3′⊕D4′G3=P3′⊕D2′⊕D3′⊕D4′(6)
根据生成的 G 3 G 2 G 1 G_3G_2G_1 G3G2G1,接收方能够判断有没有出错,是谁出错了。
海明码的检错与纠错
海明码的检错、纠错能力是有限的。由于码距是 3 3 3,因此它最多能够检测 2 2 2 位错;但是它不能区分 1 1 1 位错和 2 2 2 位错。同时,它只能够纠正 1 1 1 位错。
检测 2 2 2 位错的含义是,编码在传输过程中有 2 2 2 位出错,接收方拿到之后能够识别到异常;而不是接收方拿到数据,说我发现你发送过来的数据里面有 2 2 2 位错。
举个例子,数据传输过程中 D 1 D_1 D1 出错,接收方得到的是 G 3 G 2 G 1 = 011 G_3G_2G_1=011 G3G2G1=011;但是如果 D 2 , D 3 D_2,D_3 D2,D3 同时出错,那么接收方得到的还是 G 3 G 2 G 1 = 011 G_3G_2G_1=011 G3G2G1=011。所以只有在假定最多发生 1 1 1 位错的前提条件下,海明码才能够正确地检错并纠错。
拓展海明码
前面说了海明码不能区分
1
1
1 位错和
2
2
2 位错。如果再引入一个总偶校验位
P
a
l
l
P_{all}
Pall,就能够分辨一位错和两位错。
P
a
l
l
=
H
n
⊕
⋯
⊕
H
2
⊕
H
1
(7)
P_{all}=H_n\oplus \cdots\oplus H_2\oplus H_1\tag7
Pall=Hn⊕⋯⊕H2⊕H1(7)
G
a
l
l
=
P
a
l
l
′
⊕
H
n
′
⊕
⋯
⊕
H
2
′
⊕
H
1
′
(8)
G_{all}=P_{all}'\oplus H_n'\oplus \cdots\oplus H_2'\oplus H_1'\tag8
Gall=Pall′⊕Hn′⊕⋯⊕H2′⊕H1′(8)
( 7 ) (7) (7) 是发送方做的事情, ( 8 ) (8) (8) 是接收方做的事情。假设没有 3 3 3 位错,接收方在发现 G 3 G 2 G 1 ≠ 000 G_3G_2G_1\neq 000 G3G2G1=000 即有错的条件下,可利用 G a l l G_{all} Gall 判断是一位错 ( G a l l = 1 ) (G_{all}=1) (Gall=1) 还是两位错 ( G a l l = 0 ) (G_{all}=0) (Gall=0)。
海明码实验
海明编码
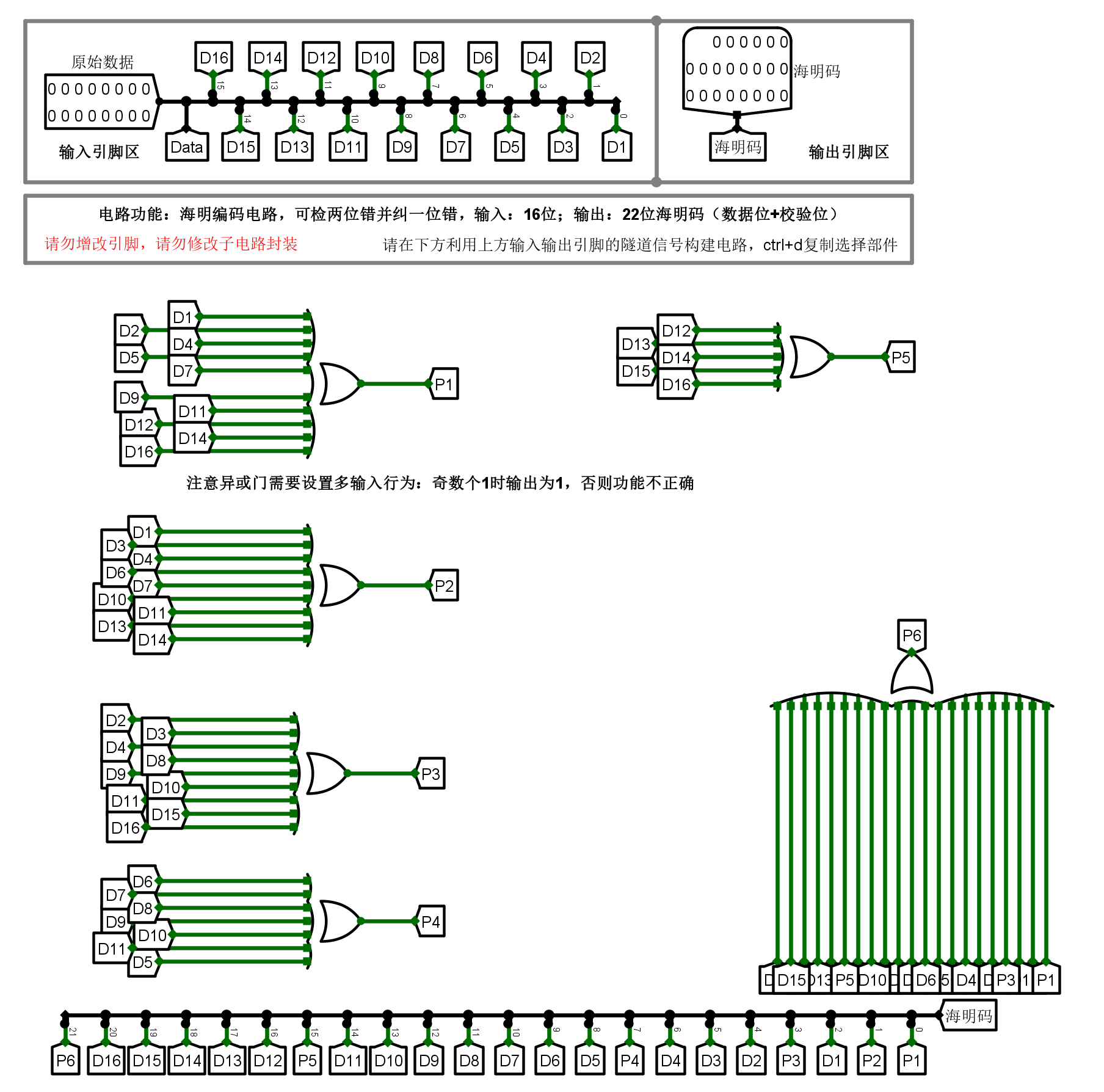
实际上就是填写分组规则表,像前文的那个表格一样。这里原始数据有
k
=
16
k=16
k=16 位,检错位有
r
=
5
r=5
r=5 位加上
1
1
1 位
P
a
l
l
(
P
6
)
P_{all}(P_6)
Pall(P6)。
P
1
P_1
P1~
P
5
P_5
P5 的线路连接参考式
(
2
)
(
5
)
(2)(5)
(2)(5),
P
6
P_{6}
P6 的线路连接参考式
(
7
)
(7)
(7)。
海明解码实验
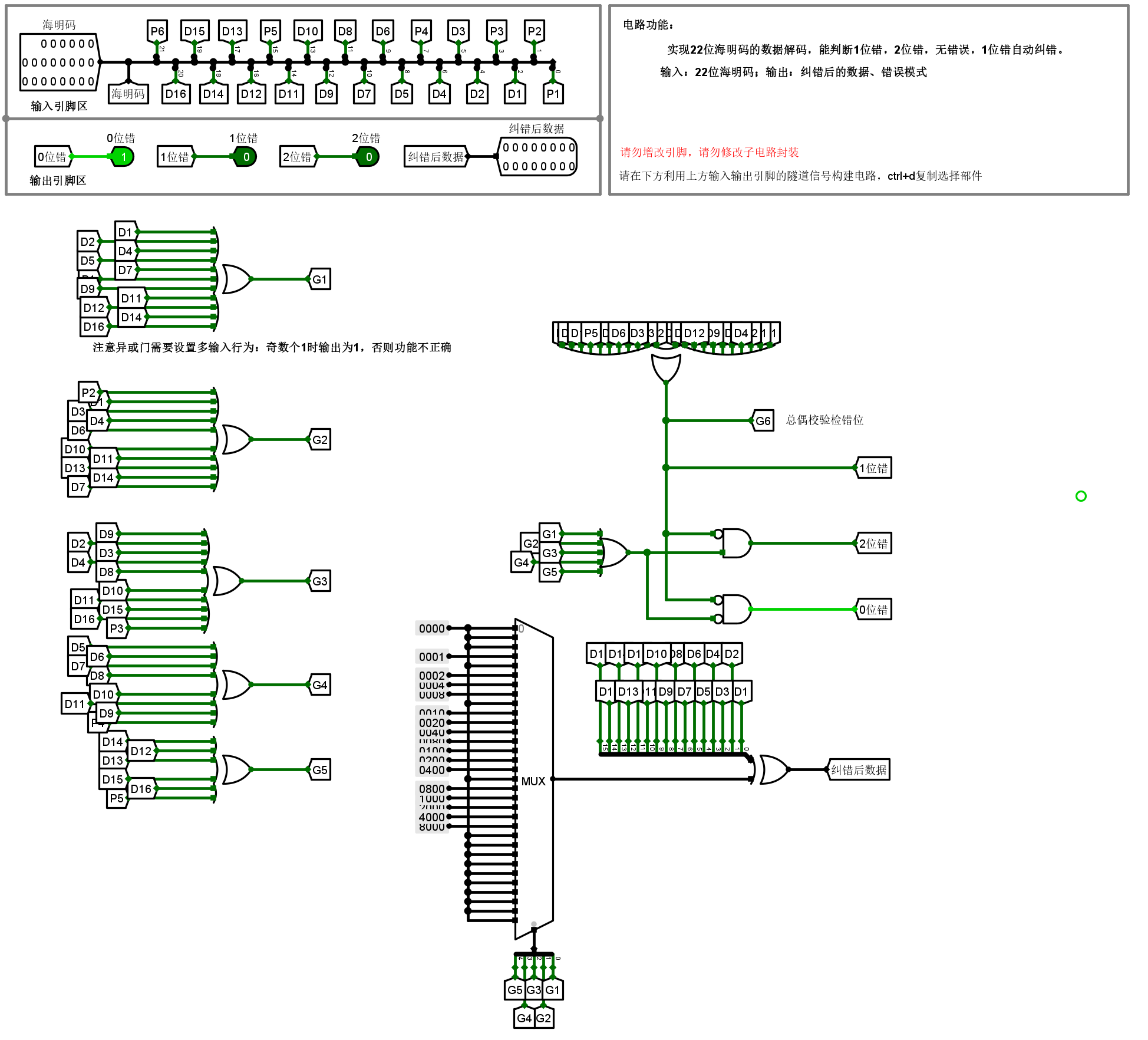
参考
(
3
)
(
6
)
(3)(6)
(3)(6),根据分组规则表生成
G
1
G_1
G1~
G
5
G_5
G5。
G
6
G_6
G6 根据
(
8
)
(8)
(8) 式生成。这里面多路选择器根据检错码
G
\boldsymbol G
G 的情况,选择一个数与原来的数据
D
\boldsymbol D
D 异或一下,使得异或的数据能够恢复成正确的数据。
资源获取
华中科技大学计算机组成原理实验
华中科技大学计算机组成原理实验——数据表示实验