因为本套题没有BFS例题,所以我先把BFS模板放着
#include<bits/stdc++.h>
using namespace std;
int n,m;//n*m的棋盘
int dis[402][402];
bool vis[402][402];
int X[]={-2,-2,-1,-1,1,1,2,2};//偏移量的表
int Y[]={-1,1,-2,2,-2,2,-1,1};//定义一个数组,我直接把这些元素从0位置填充进去
struct node{
int x;
int y;
int dis;//从起点走到当前(x,y)的最短步数
};
int st,ed;//起点x y坐标
void bfs(){
queue<node>q;
node now;
now.x=st;
now.y=ed;
now.dis=0;
q.push(now);//放入队列,第一个搜索的状态 dfs(st,ed,0)
while(!q.empty()){
//第一步取出队首状态
//第二步,弹出队首
//第三步 判断当前状态是不是已经走过了 后面再来到这个点肯定不是最短距离
//仅限于所有距离都一样的情况
//第四步 判断当前的点是不是终点
//第五步 打标记
//第六步 做相关的数据统计 比如记录(now.x,now.y)的最小步数
//第七步 以这个点拓展出去的其余状态 注意判断非法情况
}
//bfs结束
}
signed main(){
int x,y;
cin>>n>>m;
cin>>st>>ed;
//memset(dis,-1,sizeof(dis));//初始化数组
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dis[i][j]=1e9;//表示不可到达
}
}//dis[i][j]表示从起点走到(i,j)的最短距离
bfs();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
// dis[i][j]=1e9;//表示不可到达
if(dis[i][j]==1000000000)cout<<-1;
else cout<<dis[i][j];
cout<<" ";
}
cout<<'\n';
}
return 0;
}
马的便利
#include<bits/stdc++.h>
using namespace std;
struct node{
int x;
int y;
int dis;//从起点走到(x,y)的距离
};
int n,m,x,y;
int X[]={-1,-1,-2,-2,1,1,2,2};
int Y[]={2,-2,-1,1,2,-2,1,-1};
int dis[405][405];
int vis[405][405];
void bfs(){
queue<node>q;
node now;
now.x=x;
now.y=y;
now.dis=0;
q.push(now);
while(!q.empty()){
node now=q.front();
q.pop();
if(vis[now.x][now.y]==1){
continue;//已经走过这个点了
}
dis[now.x][now.y]=now.dis;
vis[now.x][now.y]=1;
node cnt;
for(int i=0;i<8;i++){
cnt.x=now.x+X[i];
cnt.y=now.y+Y[i];
cnt.dis=now.dis+1;
if(cnt.x<1||cnt.x>n||cnt.y<1||cnt.y>m)continue;
q.push(cnt);
}
}
}
int main(){
cin>>n>>m>>x>>y;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dis[i][j]=-1;
}
}
bfs();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout<<dis[i][j]<<" ";
}
cout<<'\n';
}
return 0;
}
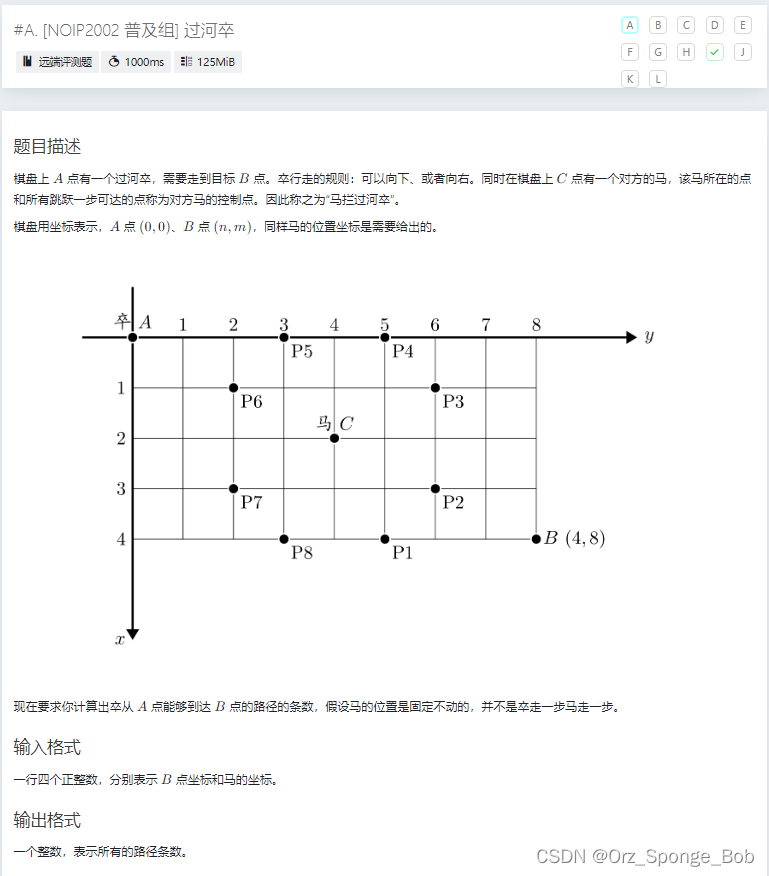
需要考虑记忆化处理
#include<bits/stdc++.h>
using namespace std;
#define int long long
int vis[30][30];
int n,m,s,b;
int dfs(int x,int y){
if(x<0||y<0)return 0;
if((x==s&&y==b)||(x==s-1&&y==b-2)||(x==s-2&&y==b-1)||(x==s-2&&y==b+1))return 0;
if((x==s-1&&y==b+2)||(x==s+1&&y==b+2)||(x==s+2&&y==b+1)||(x==s+2&&y==b-1)||(x==s+1&&y==b-2))return 0;
if(x==0&&y==0)return 1;
if(vis[x][y])return vis[x][y];
return vis[x][y]=dfs(x-1,y)+dfs(x,y-1);
}
signed main() {
cin>>n>>m>>s>>b;
cout<<dfs(n,m);
return 0;
}
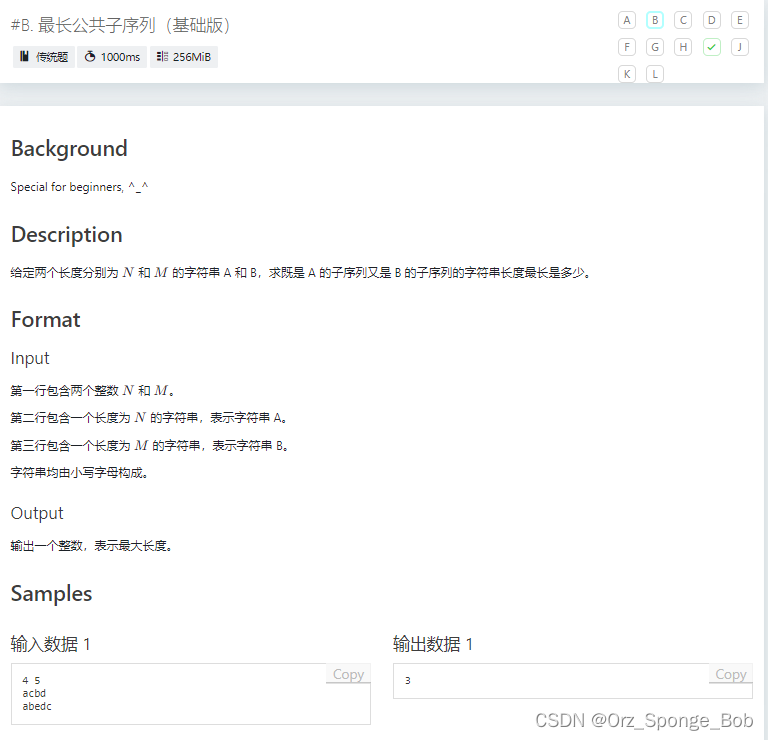
#include<bits/stdc++.h>
using namespace std;
char A[1005];
char B[1005];
int dp[1005][1005];
int main(){
int n,m;
cin>>n>>m;
cin>>A+1>>B+1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(A[i]==B[j]){
dp[i][j]=dp[i-1][j-1]+1;
}
else{
dp[i][j]=max(dp[i-1][j-1],max(dp[i-1][j],dp[i][j-1]));
}
}
}
cout<<dp[n][m];
return 0;
}
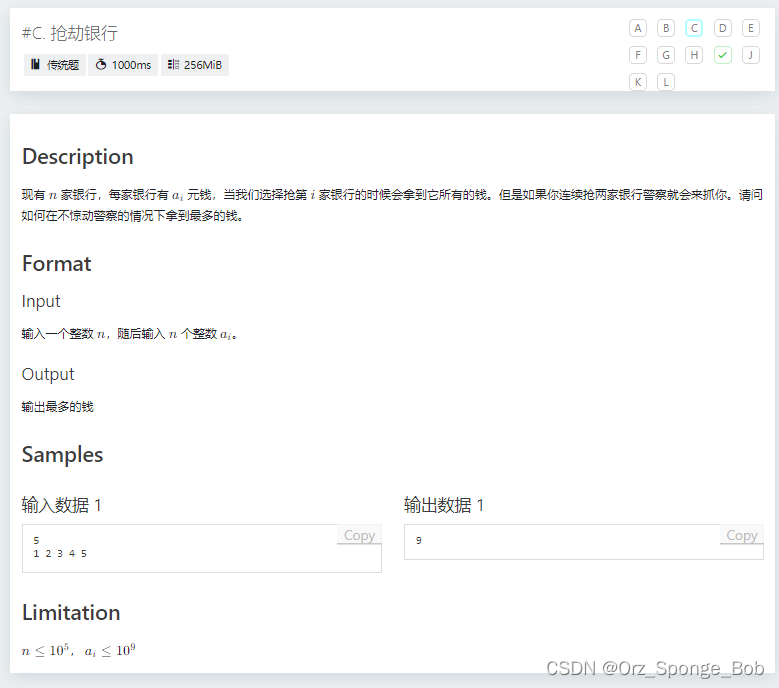
#include<bits/stdc++.h>
using namespace std;
long long dp[100005][2];
int main() {
int n;
cin>>n;
//dp[0][0]=dp[0][]
//dp[i][0] 没抢i银行
for(int i=1;i<=n;i++){
long long x;
cin>>x;
// cout<<i<< " ";
dp[i][0]=max(dp[i-1][0],dp[i-1][1]);//没抢
dp[i][1]=dp[i-1][0]+x;
// cout<<dp[i][0]<<" "<<dp[i][1]<<'\n';
}
cout<<max(dp[n][0],dp[n][1]);
return 0;
}
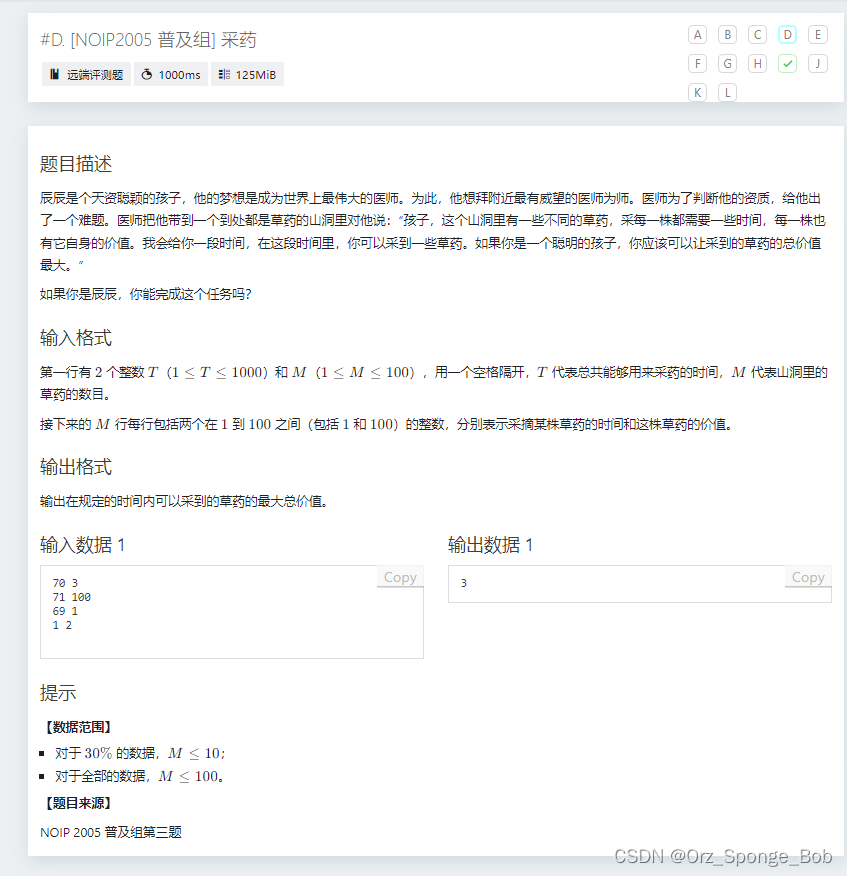
物品只拿一次,01背包
#include<bits/stdc++.h>
using namespace std;
int V[1005],W[1005];//
int dp[1005];
//有一大堆财宝,体积分别是V[i] 价值是W[i]
//你现在有一个体积为M的包,你想知道怎么样拿 能保证 在背包容量的限制下 拿到最多价值的财宝
signed main(){
//总背包容量10
//只考虑拿价值高的 价值是10,体积是10 可能有其他财宝价值5 体积1 有若干个
//dfs(拿/不拿) 暴力 n<=20
/*背包dp 01背包
dp[i][j] 表示处理完前i个物品 有j的容量
单独考虑处理第i个物品,那么是不是跟dp[i-1][] + 如何处理第i个物品=> dp[i][] 有关联
如果第i个物品你要拿
因为你拿了第i个物品,体积变大,变成了dp[i][j]
dp[i][j] = dp[i-1][j-V[i]] + W[i]
如果我们不拿第i个物品 变到了dp[i][j]
dp[i][j] =dp[i-1][j]
?????我们的容量j
dp[i][j] =max(dp[i-1][j],dp[i-1][j-V[i]]+W[i]);
// j=?+V[i]
*/
int M,n;
cin>>M>>n;//M是总体积 n是物品个数
for(int i=1;i<=n;i++){
cin>>V[i]>>W[i];//输入体积 和 价值
}
for(int i=1;i<=n;i++){
for(int j=M;j>=V[i];j--){
dp[j]=max(dp[j],dp[j-V[i]]+W[i]);
}
}
cout<<dp[M];
return 0;
}
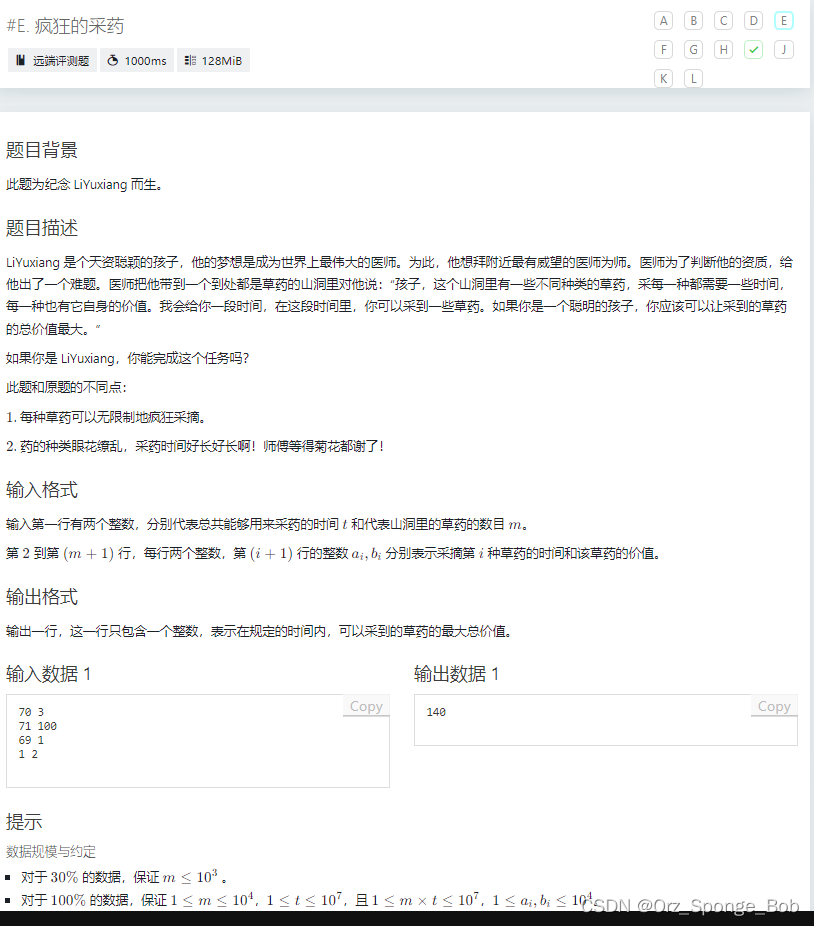
#include<bits/stdc++.h>
using namespace std;
long long T,M,t[10001],v[10001],dp[10000001];
int main(){
cin>>T>>M;
for(int i=1;i<=M;i++)
cin>>t[i]>>v[i];
for(int i=1;i<=M;i++)
for(int j=t[i];j<=T;j++)
dp[j]=max(dp[j],dp[j-t[i]]+v[i]);
cout<<dp[T];
return 0;
}
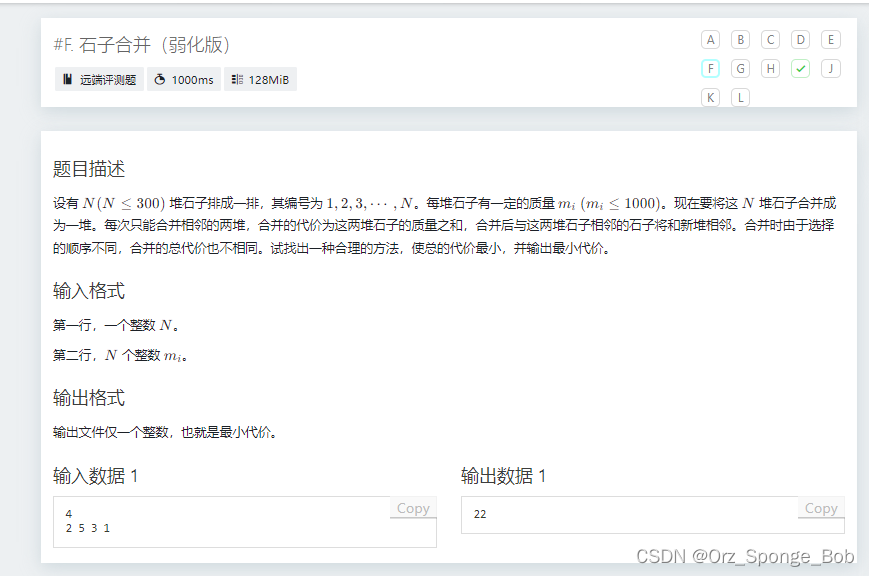
#include<bits/stdc++.h>
using namespace std;
int dp[305][305];
int w[305];
int sum[305];
signed main(){
/* 考虑区间dp
dp[l][r]= 表示把[L,R]的石头合并成一堆所需要的最小花费
考虑转移
1 1 1 1 1 1 1
所有大的区间一定由小区间转移
考虑合并成长度为2的区间
// dp[i][i+1]=(dp[i][i]+dp[i+1][i+1])+w[i]+w[i+1]
合并成3区间 来自于长度为2 + 拼长度为1
长度为4的区间 1+3 2+2 3+1 ....
考虑dp[l][r] 拆成两个区间,进行合并 */
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>w[i];
sum[i]=sum[i-1]+w[i];//前缀和
}
for(int len=1;len<=n;len++){
for(int i=1;i<=n;i++){
//i作为区间起点
//枚举区间长度
//计算右端点在哪
int j=i+len;
dp[i][j]=1e9;
if(j>n)break;
for(int k=i;k<j;k++){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]);
}
}
}
cout<<dp[1][n];
return 0;
}
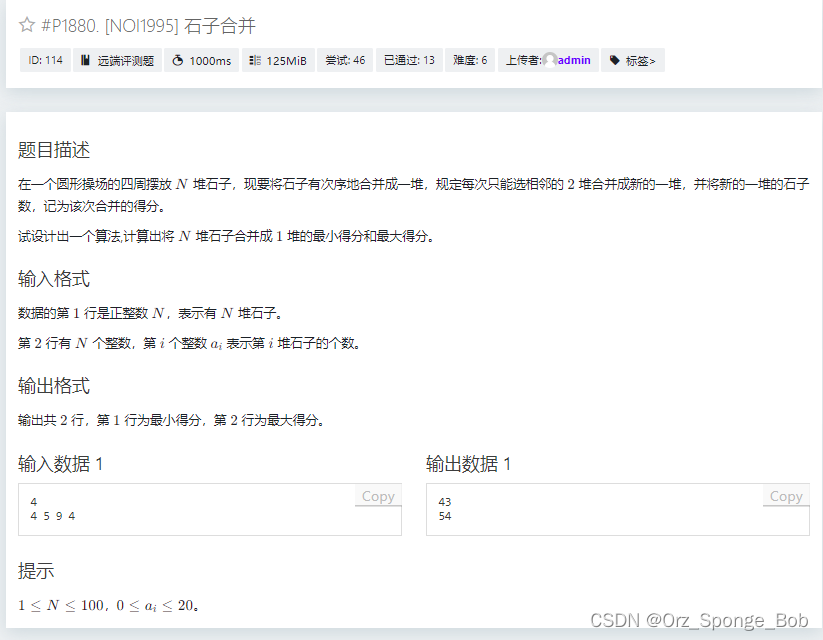
#include<bits/stdc++.h>
using namespace std;
int n;
int minx = 0x3f3f3f3f,maxn = -1;
int s[305];
int m[305];
int dp1[305][305];
int dp2[305][305];
int main()
{
cin >> n;
for(int i = 1; i <= n; i++){
cin >> m[i];
m[i + n] = m[i];
}
memset(dp1,0x3f3f3f3f,sizeof(dp1));
memset(dp2,-1,sizeof(dp2));
for(int i = 1; i <= n * 2; i++){
s[i] = s[i - 1] + m[i];
dp1[i][i] = 0;
dp2[i][i] = 0;
}
for(int i = 2; i <= n; i++){
for(int l = 1; l <= n * 2 - i + 1; l++){
int r = l + i - 1;
for(int j = l; j < r; j++){
dp1[l][r] = min(dp1[l][r],dp1[l][j] + dp1[j + 1][r]);
dp2[l][r] = max(dp2[l][r],dp2[l][j] + dp2[j + 1][r]);
}
dp1[l][r] += (s[r] - s[l - 1]);
dp2[l][r] += (s[r] - s[l - 1]);
}
}
for(int i = 1; i <= n; i++){
minx = min(minx,dp1[i][i + n - 1]);
maxn = max(maxn,dp2[i][i + n - 1]);
}
cout << minx << "\n" << maxn;
return 0;
}
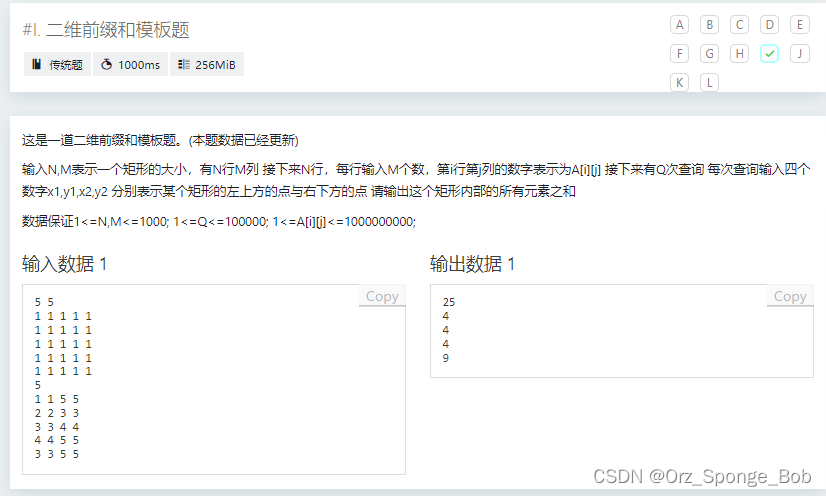
注意输出格式啊。。。。注意数据类型 long long
#include <bits/stdc++.h>
using namespace std;
int n, m;
int a[1005][1005];
long long sum[1005][1005];
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
cin >> a[i][j];
}
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
}
}
int q; cin >> q;
while(q--) {
int X1, Y1, X2, Y2;
cin >> X1 >> Y1 >> X2 >> Y2;
cout << sum[X2][Y2] - sum[X1 - 1][Y2] - sum[X2][Y1 - 1] + sum[X1 - 1][Y1 - 1] << '\n';
}
return 0;
}

#include<bits/stdc++.h>
using namespace std;
int a[100005];
long long int pre[100005];
long long int sum[100005];
int main()
{
int n;
scanf("%d",&n);
for(int i=1; i<=n; i++)
{
scanf("%d",&a[i]);
pre[i]=a[i]-a[i-1];
}
//1 2 3 4 5
//+2 -2
//+3 -3
int m;
scanf("%d",&m);
while(m--)
{
int l,r,x;
scanf("%d%d%d",&l,&r,&x);
pre[l]+=x;
pre[r+1]-=x;
}
int st,ed;
scanf("%d%d",&st,&ed);
long long int ans=0;
long long int cnt=0;
for(int i=1;i<=n;i++){
sum[i]=sum[i-1]+pre[i];
}
for(int i=st; i<=ed; i++)
{
ans+=sum[i];
}
printf("%lld",ans);
}

#include<bits/stdc++.h>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define all(x) x.begin(),x.end()
using namespace std;
const double eps=1e-8;
const double PI=acos(-1.0);
typedef long long ll;
template<class T>int chkmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>int chkmax(T &a,T b){return a<b?a=b,1:0;}
template<class T>T sqr(T a){return a*a;}
template<class T>T mmin(T a,T b){return a<b?a:b;}
template<class T>T mmax(T a,T b){return a>b?a:b;}
template<class T>T aabs(T a){return a<0?-a:a;}
#define min mmin
#define max mmax
#define abs aabs
int a[1024][1024];
int main(){
#ifdef cnyali_lk
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
int n,m,xa,ya,xb,yb;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d%d%d%d",&xa,&ya,&xb,&yb);
++a[xa][ya];
--a[xb+1][ya];
--a[xa][yb+1];
++a[xb+1][yb+1];
}
for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)printf("%d%c",a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1],j==n?'\n':' ');
return 0;
}
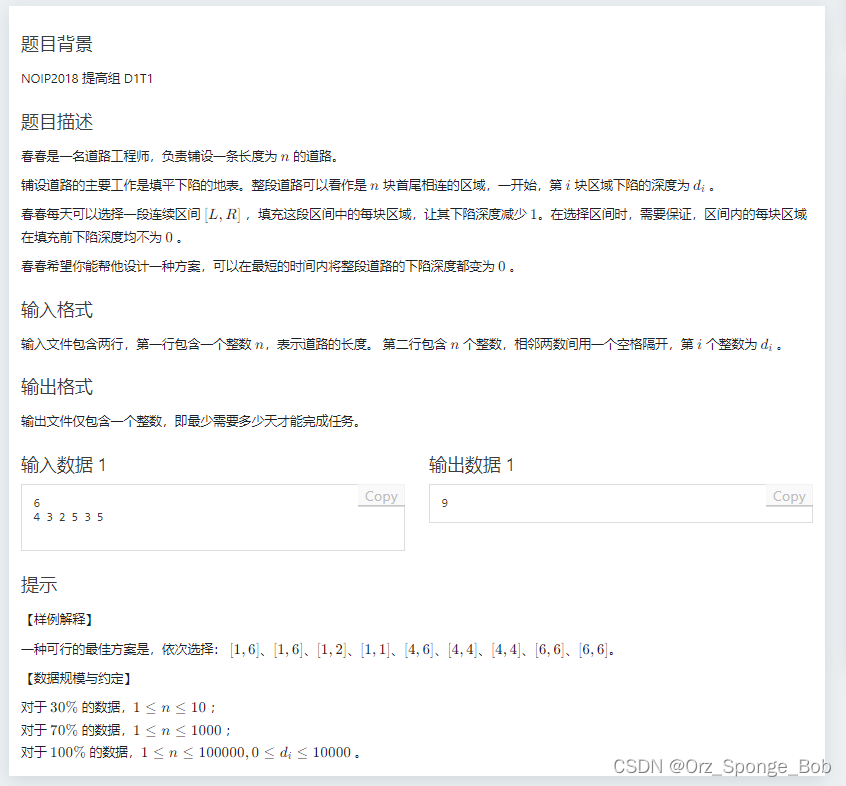
答案 A【1】+ 枚举i=2~n 里面所有的A[i]>A[i-1] 的情况的差