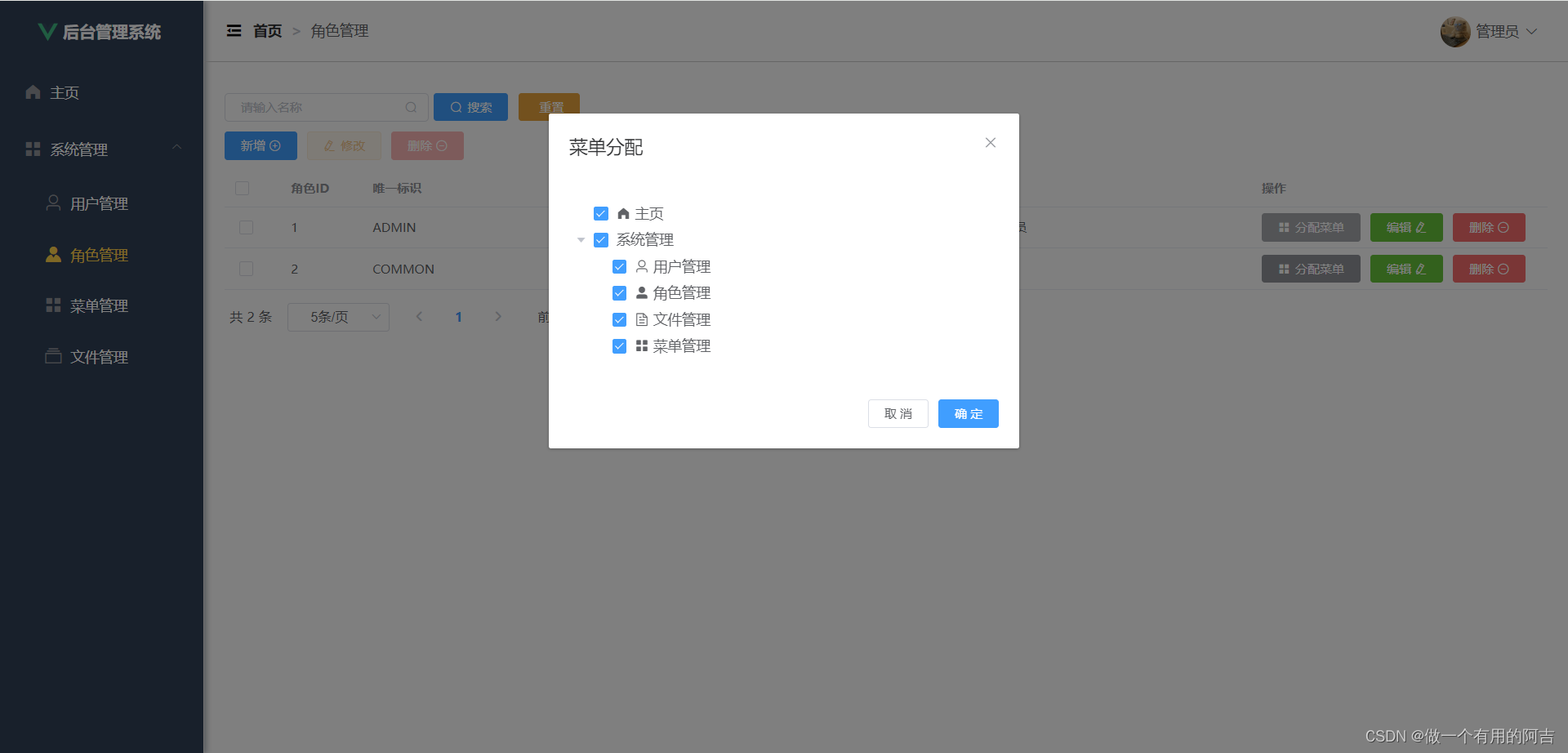
一、问题描述
三次样条插值的实现。
二、实验目的
掌握三次样条插值方法的原理,能够编写代码获得自然、抛物线端点以及非纽结三次样条。
三、实验内容及要求
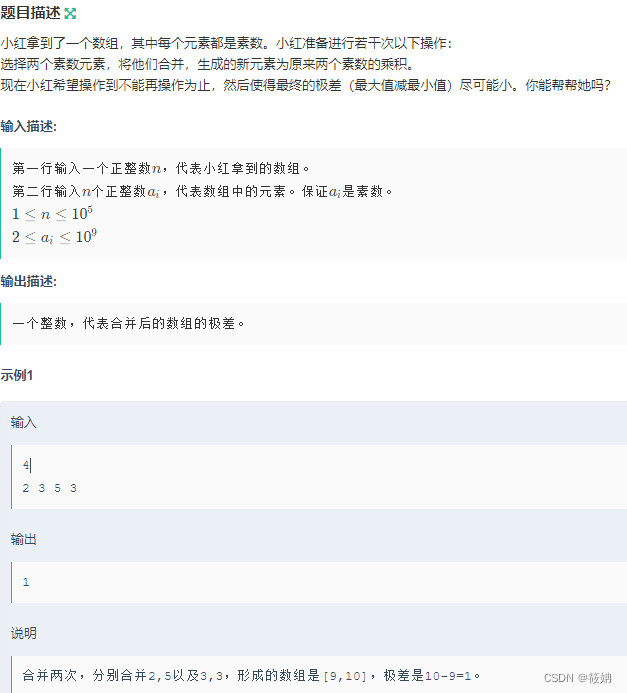
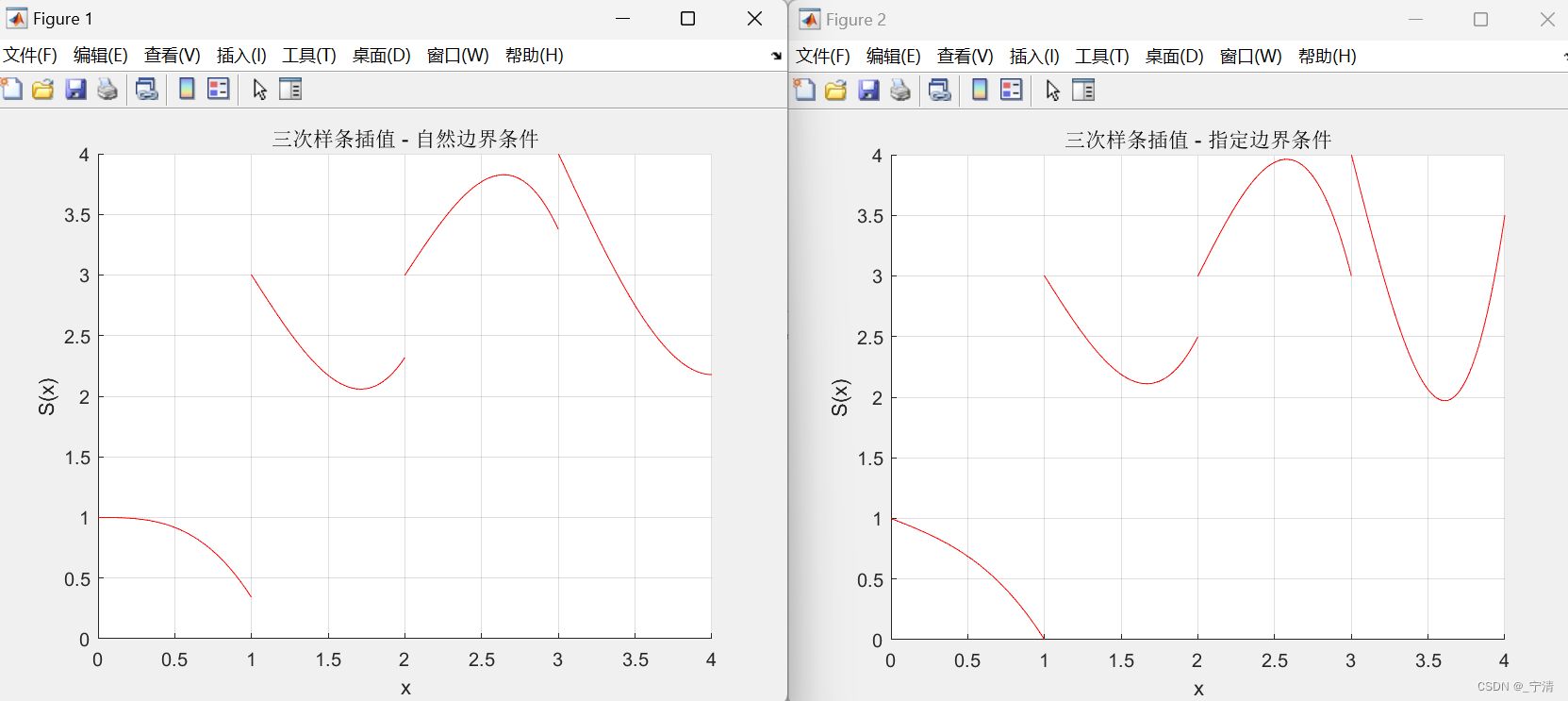
- 找出并画出三次样条S,满足S(0) = 1, S(1) = 3, S(2) = 3, S(3) = 4, S(4) = 2,其中边界条件分别设置为自然、抛物线端点以及非纽结。
- 找出并画出三次样条S,满足S(0) = 1, S(1) = 3, S(2) = 3, S(3) = 4, S(4) = 2,其中边界条件分别设置为S’‘(0)=3, S’'(4)=2。
四、算法原理
- 给出三次样条函数的的具体形式,及合格的三次样条函数需要满足的三大组性质。
- 如何获得自然三次样条、抛物线端点的三次样条、非纽结三次样条中的未知系数?
1. 三次样条函数的具体形式及性质
三次样条函数的形式:
在区间 [ x i , x i + 1 ] [x_i, x_{i+1}] [xi,xi+1] 上,三次样条函数 S i ( x ) S_i(x) Si(x)的一般形式为:
S i ( x ) = a i + b i ( x − x i ) + c i ( x − x i ) 2 + d i ( x − x i ) 3 S_i(x) = a_i + b_i(x - x_i) + c_i(x - x_i)^2 + d_i(x - x_i)^3 Si(x)=ai+bi(x−xi)+ci(x−xi)2+di(x−xi)3
其中, a i , b i , c i , d i a_i, b_i, c_i, d_i ai,bi,ci,di 是系数,需要通过一系列的性质和条件来确定。
三大组性质:
为了确保三次样条插值的平滑性和连续性,三次样条函数需要满足以下三大组性质:
-
插值性质: 保证插值点上的函数值与原始数据点一致。
S i ( x i ) = y i S_i(x_i) = y_i Si(xi)=yi
S i ( x i + 1 ) = y i + 1 S_i(x_{i+1}) = y_{i+1} Si(xi+1)=yi+1 -
平滑性质: 保证相邻区间的两个三次样条函数在插值点处的一阶和二阶导数相等。
S i ′ ( x i + 1 ) = S i + 1 ′ ( x i + 1 ) S'_i(x_{i+1}) = S'_{i+1}(x_{i+1}) Si′(xi+1)=Si+1′(xi+1)
S i ′ ′ ( x i + 1 ) = S i + 1 ′ ′ ( x i + 1 ) S''_i(x_{i+1}) = S''_{i+1}(x_{i+1}) Si′′(xi+1)=Si+1′′(xi+1) -
端点条件: 根据实际问题选择边界条件,常见的有自然边界条件、抛物线端点条件、非纽结条件等。
2. 获得未知系数的方法
自然三次样条:
- 由插值性质得到 (n-1) 个方程。
- 由平滑性质得到 (n-2) 个方程(去掉两个端点)。
- 自然边界条件提供两个方程。
- 共 (3n - 3) 个方程,解 (3n - 3) 个未知数。
抛物线端点的三次样条:
- 由插值性质得到 (n-1) 个方程。
- 由平滑性质得到 (n-2) 个方程。
- 抛物线端点条件提供两个方程。
- 共 (3n - 3) 个方程,解 (3n - 3) 个未知数。
非纽结三次样条:
- 由插值性质得到 (n-1) 个方程。
- 由平滑性质得到 (n-2) 个方程。
- 根据非纽结条件提供 (n-2) 个方程。
- 共 (3n - 3) 个方程,解 (3n - 3) 个未知数。
求解未知系数:
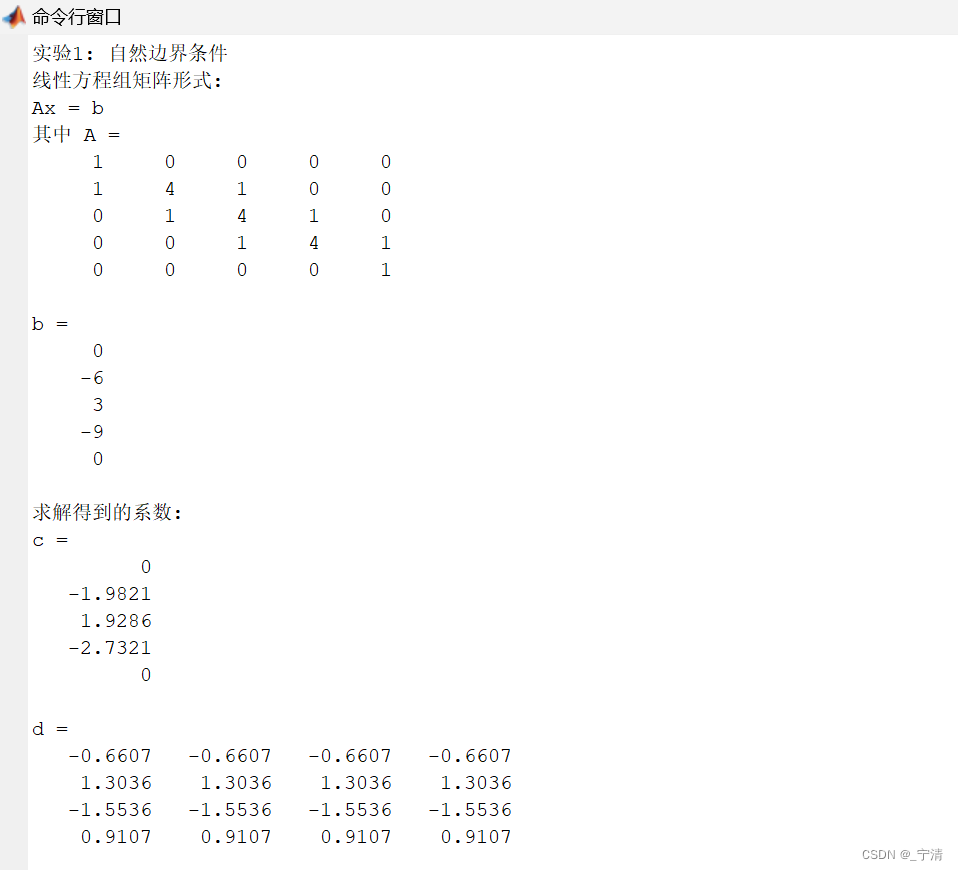
以上得到的方程组可以写成矩阵形式 A x = b Ax = b Ax=b,其中 A A A 是系数矩阵, x x x 包含 a i , b i , c i , d i a_i, b_i, c_i, d_i ai,bi,ci,di 的向量, b b b 是右侧常数向量。通过求解这个线性方程组,可以得到三次样条函数的所有未知系数。
五、测试数据及结果
对于两道题目,分别给出求解系数c 时的线性方程组的矩阵形式,然后给出求出的b、c、d 三组系数。

六、总结与思考
在完成三次样条插值的实验过程中,我获得了许多关于插值方法和 MATLAB 编程的经验。以下是我的总结和思考:
1. 三次样条插值的原理理解:
通过这个实验,我更深入地理解了三次样条插值的原理。三次样条插值是一种通过分段定义的三次多项式来逼近原始数据的方法。理解插值、平滑和端点条件的关系对正确实现算法至关重要。
2. MATLAB 编程技巧:
在编写 MATLAB 代码的过程中,我学到了一些有关函数文件和主文件的组织结构的技巧。将不同功能的代码模块化,使用函数文件进行封装,有助于提高代码的可读性和维护性。同时,注释的使用也对代码的理解和他人阅读提供了帮助。
3. 线性方程组求解:
实验中需要解一个线性方程组来获得三次样条插值的系数。MATLAB 中有强大的线性代数库,使用反斜杠运算符(\)可以很方便地解决线性方程组。理解这一点对于处理插值问题和其他需要解线性方程组的情况都是非常有用的。
4. 实验中的边界条件选择:
实验中涉及到了不同的边界条件,包括自然边界条件、抛物线端点条件和非纽结条件。根据具体问题选择合适的边界条件对于得到符合实际情况的插值结果至关重要。深入理解每种边界条件的含义和适用场景是提高实验准确性的关键。
5. 对问题的思考和解决:
实验中还涉及到一些错误和问题,例如代码报错等。对这些问题进行仔细的思考和排查是解决问题的关键。通过查阅文档、调试代码和阅读错误信息,我更加熟悉了问题定位和解决的过程。
通过这次实验,我不仅学到了有关三次样条插值的知识,还提高了在 MATLAB 中编写科学计算代码的能力。这种实践不仅加深了我对插值方法的理解,也提高了我的编程水平和问题解决能力。在今后的学习和工作中,我将继续积累经验,不断提升自己在数值分析和科学计算领域的能力。