看到大厂工时爆料，我沉默了。。

news2025/1/10 23:47:28

大厂工时爆料

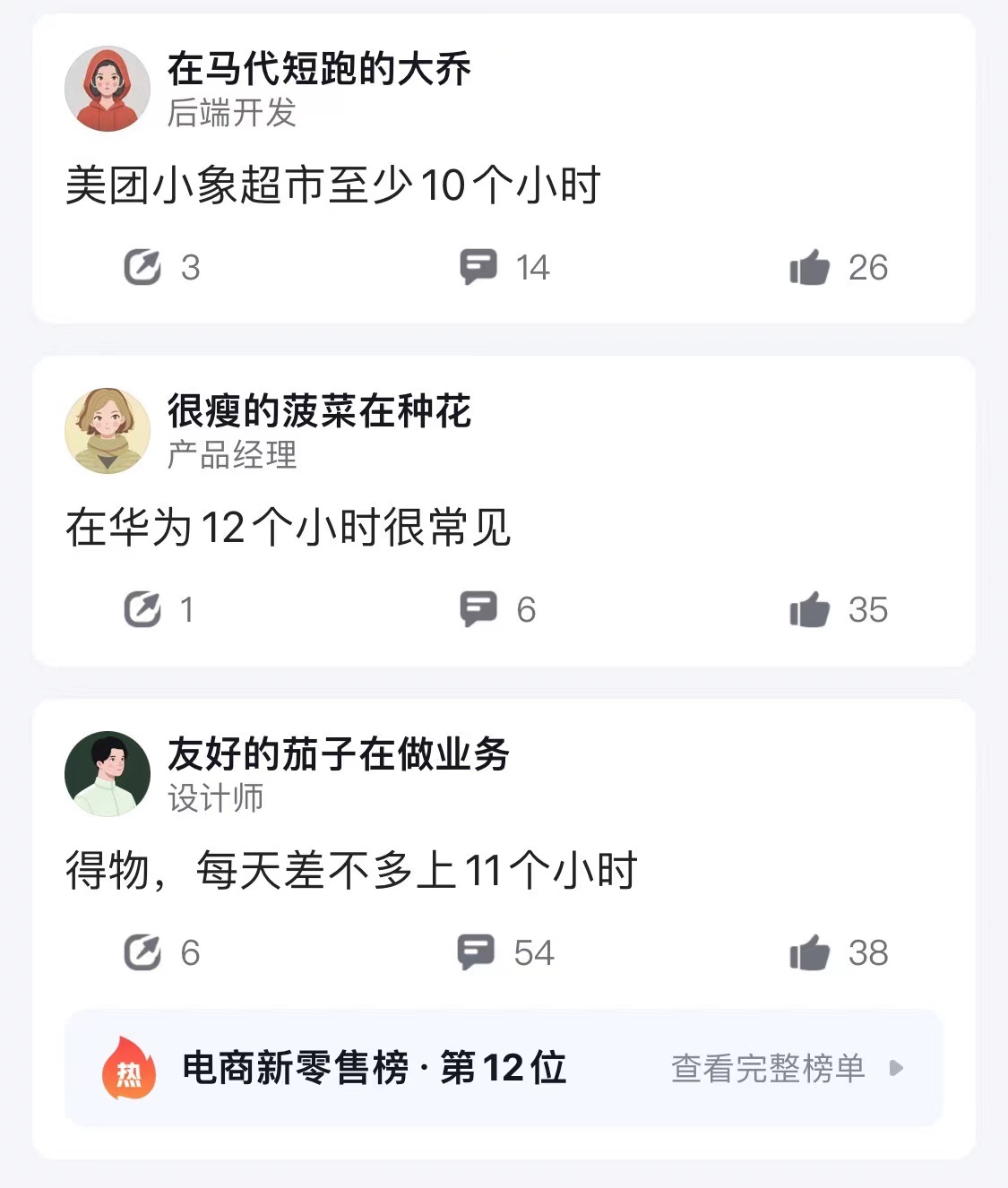
今天逛脉脉的时候，看到一篇名为「一人一句，大厂工时爆料」的帖子：

点开之后，我沉默了 ...

出来爆料的基本上都是 10+ 小时。

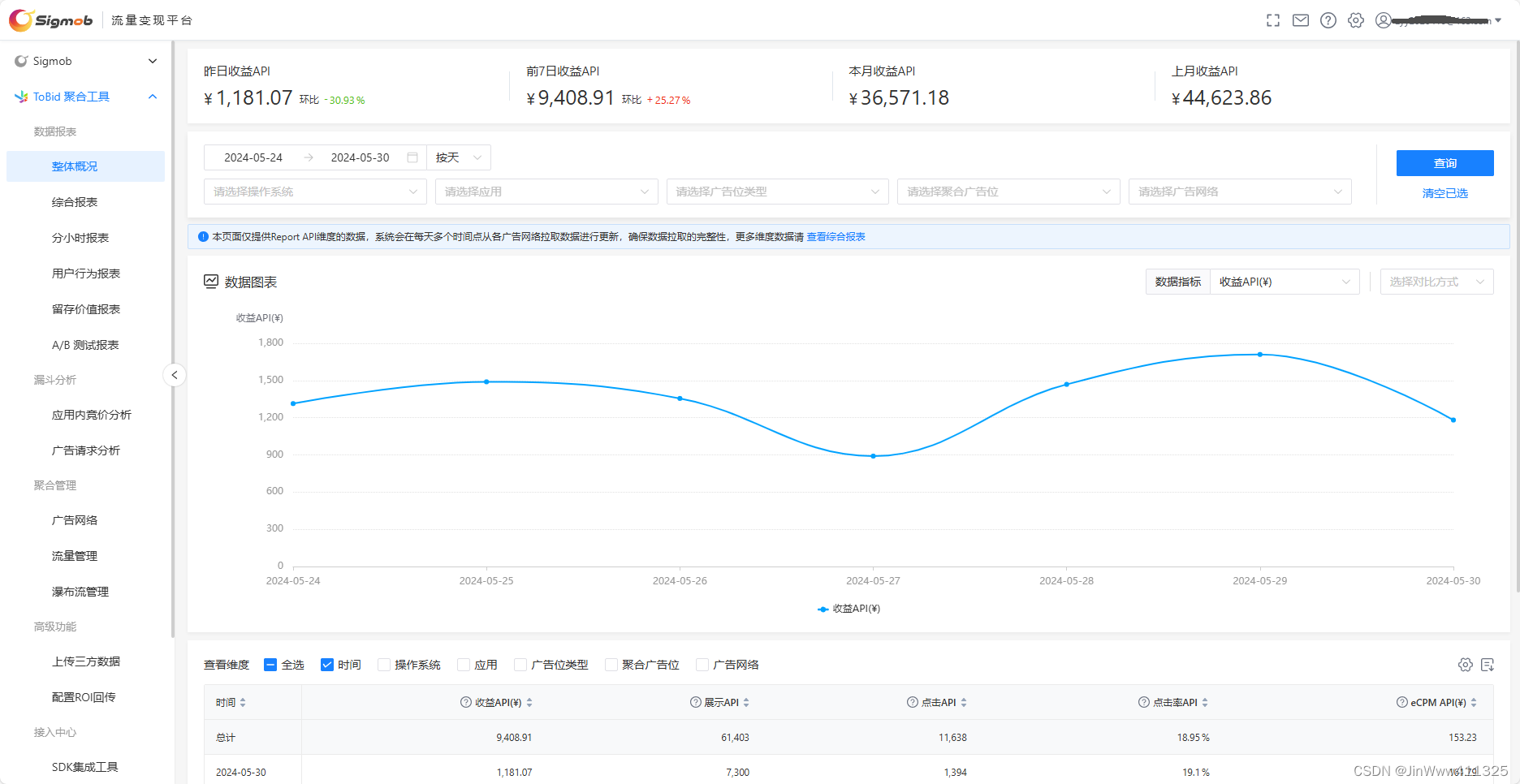
好奇心之下，我搜索了一下去年很热的排行榜：

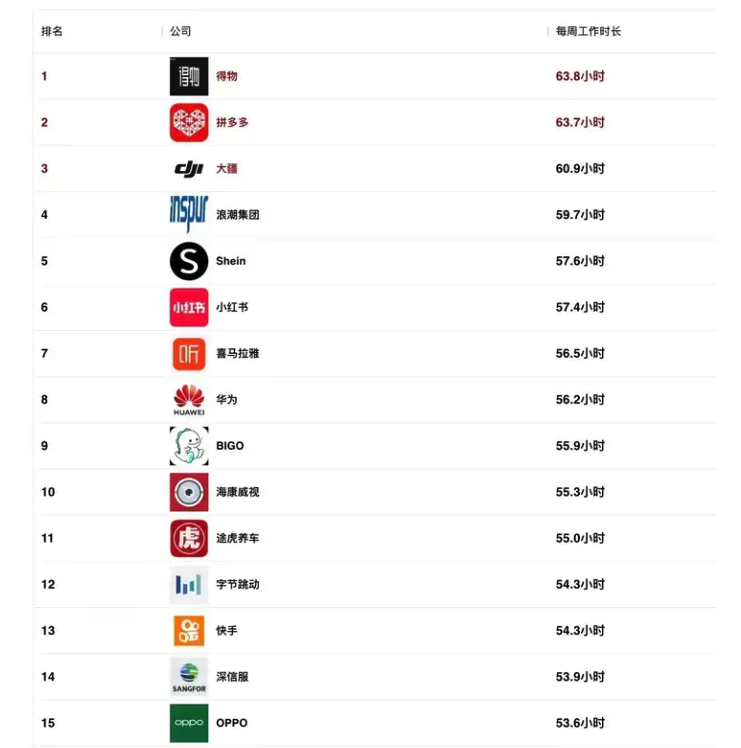
好家伙，依然稳定。

如果是偶尔赶项目，加班一下能理解，去年周工作时长已经长达 60+ 小时，今年还被爆料日均 10+ 个小时，说明内卷已经成为日常了。

过去几年，各行各业都羡慕计算机行业，但大多围城外的人只看到巨额年终，而看不到超低时薪。

对此，你怎么看？欢迎新建「匿名身份」在评论区爆料你的工时（貌似还很多同学不知道公众号新出的这功能，有段时间了

...

回归主题。

来一道不算容易的，和「字节跳动（社招四面）」相关的题目。

题目描述

平台：LeetCode

题号：862

给你一个整数数组 nums 和一个整数 k ，找出 nums 中和至少为 k 的最短非空子数组，并返回该子数组的长度。

如果不存在这样的子数组，返回 -1 。

子数组是数组中连续的一部分。

示例 1：

输入：nums = [1], k = 1

输出：1

示例 2：

输入：nums = [1,2], k = 4

输出：-1

示例 3：

输入：nums = [2,-1,2], k = 3

输出：3

提示：

前缀和 + 离散化 + 权值树状数组

由于求解的对象是子数组，容易联想到求连续段之和，容易联想到「前缀和」，假设我们预处理出的前缀和数组为 sum（为了方便，我们令前缀和数组坐标从 1 开始）。

即每个而言，本质上是找满足「」条件的最大下标 j，其中 j 的取值范围为，从而知道以 i 作为右端点时，满足条件的最短子数组长度为。

先考虑存在负数域的问题，由于我们需要使用，以及对应的，同时 k 的取值为（过大），我们可以通过「离散化」手段将其映射到 2 倍的数组长度，即大小为的正数域。

随后来考虑如何求解「满足条件的最大下标」问题，可以通过「权值树状数组」来做：对于每个而言，我们利用「权值树状数组」来维护满足大于等于的最大下标。起始我们先初始化树状数组为 -1，遍历过程中，查询是否存在满足条件的下标（若不为 -1 则更新 ans），并更新权值树状数组对应的最大下标即可。

Java 代码：

class Solution {
    static int N = 200010;
    static int[] tr = new int[N], sum = new int[N];
    int n, m, ans;
    int lowbit(int x) {
        return x & -x;
    }
    void update(int val, int loc) {
        for (int i = val; i < m; i += lowbit(i)) tr[i] = Math.max(tr[i], loc);
    }
    int query(int x) {
        int ans = -1;
        for (int i = x; i > 0; i -= lowbit(i)) ans = Math.max(ans, tr[i]);
        return ans;
    }
    int getIdx(List<Long> list, long x) {
        int l = 0, r = list.size() - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (list.get(mid) >= x) r = mid;
            else l = mid + 1;
        }
        return r + 1;
    }
    public int shortestSubarray(int[] nums, int k) {
        n = nums.length; m = 2 * n + 10; ans = n + 10;
        Arrays.fill(tr, -1);
        long[] temp = new long[m];
        List<Long> list = new ArrayList<>();
        list.add(0L);
        for (int i = 1; i <= 2 * n + 1; i++) {
            if (i <= n) temp[i] = temp[i - 1] + nums[i - 1];
            else temp[i] = temp[i - (n + 1)] + k;
            list.add(temp[i]);
        }
        Collections.sort(list);
        for (int i = 0; i <= 2 * n + 1; i++) sum[i] = getIdx(list, temp[i]);
        update(sum[n + 1], 0);
        for (int i = 1; i <= n; i++) {
            int j = query(sum[i]);
            if (j != -1) ans = Math.min(ans, i - j);
            update(sum[n + 1 + i], i);
        }
        return ans == n + 10 ? -1 : ans;
    }
}

C++ 代码：

class Solution {
public:
    static const int N = 200010;
    vector<int> tr, sum;
    int n, m, ans;
    int lowbit(int x) {
        return x & -x;
    }
    void update(int val, int loc) {
        for (int i = val; i < m; i += lowbit(i)) tr[i] = max(tr[i], loc);
    }
    int query(int x) {
        int ans = -1;
        for (int i = x; i > 0; i -= lowbit(i)) ans = max(ans, tr[i]);
        return ans;
    }
    int shortestSubarray(vector<int>& nums, int k) {
        n = nums.size(); m = 2 * n + 10; ans = n + 10;
        tr.resize(m, -1); sum.resize(m + 10, 0);
        vector<long long> temp(m);
        vector<long long> list;
        for (int i = 1; i <= 2 * n + 1; i++) {
            if (i <= n) temp[i] = temp[i - 1] + nums[i - 1];
            else temp[i] = temp[i - (n + 1)] + k;
            list.push_back(temp[i]);
        }
        sort(list.begin(), list.end());
        for (int i = 0; i <= 2 * n + 1; i++) {
            sum[i] = lower_bound(list.begin(), list.end(), temp[i]) - list.begin() + 1;
        }
        update(sum[n + 1], 0);
        for (int i = 1; i <= n; i++) {
            int j = query(sum[i]);
            if (j != -1) ans = min(ans, i - j);
            update(sum[n + 1 + i], i);
        }
        return ans == n + 10 ? -1 : ans;
    }
};