前言:
说到桶排序,那必定要有桶,那么桶的作用是什么呢?桶的作用就是将序列分为若干份放到桶中,每个桶中能装入的数量范围是一定的,只有最后一个桶可以设置装入很多。这是因为当分的桶一定时,前面的桶装入的数的范围有限,这时还有序列中的数大于最后一个桶的数值范围,就把多余的装到最后一个桶中。
那么如何把序列一个个放入不同的桶中呢,好比有从1到100这么多个数,我们要怎么分桶,分多少桶,可以根据序列的性质来设置。可以分10个桶,然后每个桶就是装10个数的范围,第一个桶装1-10的数,第二个桶装11-20的数,......,第十个桶装91-100的数,当然若有超过100的数由于没有第十一个桶,我们就把它装入第十个桶中。由此可知,每个桶装一定范围的数。
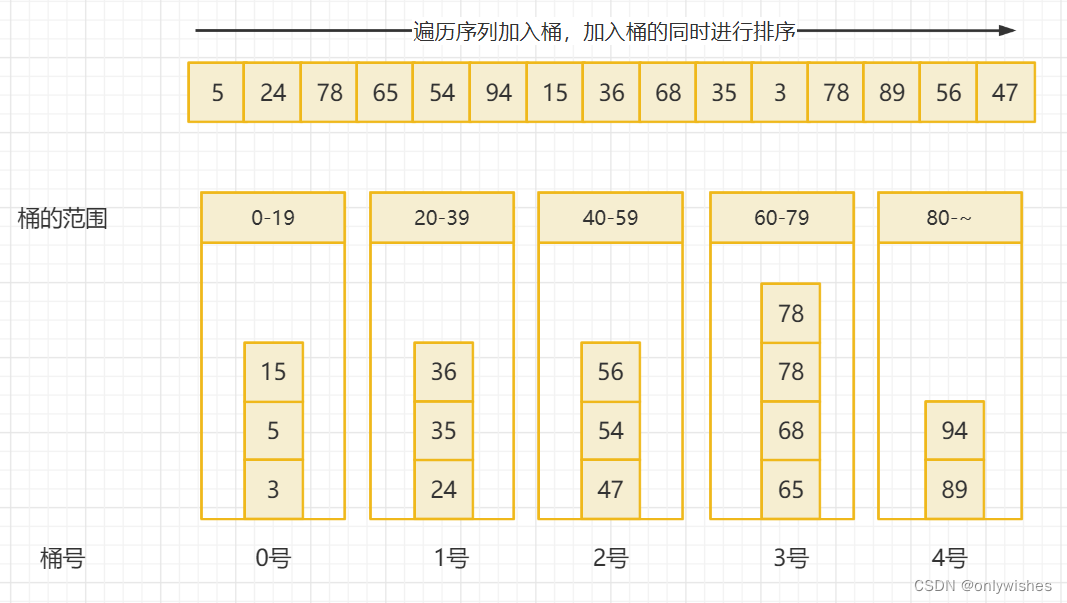
把序列装入桶中就完了么,当然不是,还没有排序呢。这里当把一个序列装入桶中时,就用插入排序,从后往前插入,如果该数比前面的数大就插入其后面,不然就向前比较插入。就是说桶中每插入一个数就会把该数放到合适的位置使桶整体有序。
最后就是按顺序逐个把每个桶中的元素放回原来的序列中。
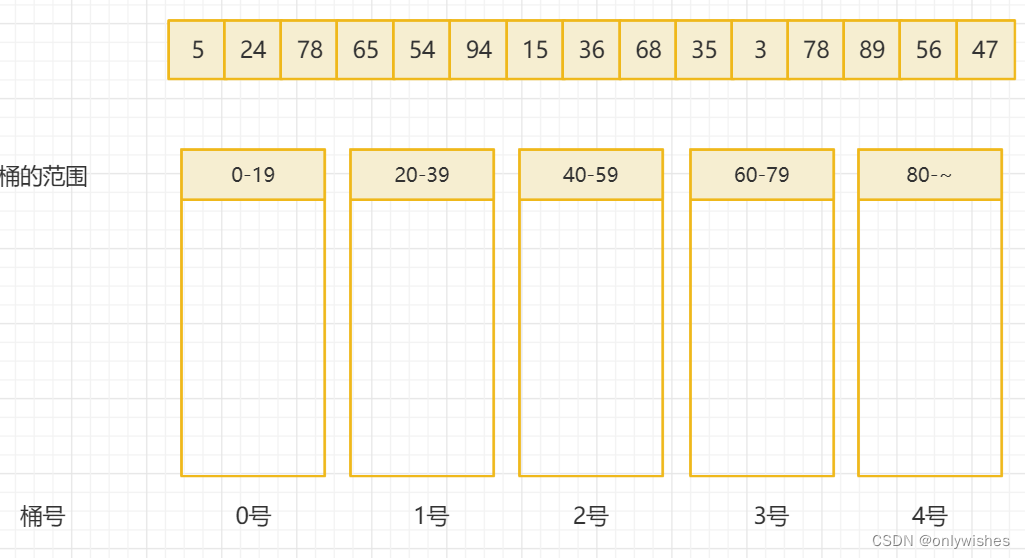
如下图,我们以序列【5, 24, 78, 65, 54, 94, 15, 36, 68, 35, 3, 78, 89, 56, 47】为例,进行桶排序。可以分配5个桶,每个桶中包含20个数的范围。
实现代码:
def BucketSort(li, n=100, max_num=10000):
buckets = [[] for _ in range(n)] #创建桶
for var in li:
i = min(var // (max_num // n), n-1) # i 表示当前的数(var)放到几号桶里,最后一个桶是最大的一段数
buckets[i].append(var) #把var加到对应的桶里面
#保持桶内的顺序
for j in range(len(buckets[i])-1, 0, -1): # 从最后一个位置往前比较
if buckets[i][j] < buckets[i][j-1]:
buckets[i][j], buckets[i][j-1] = buckets[i][j-1], buckets[i][j]
else:
break
# 把桶内数据放回原序列
li.clear()
for buc in buckets: #每个桶内都是有序的,连接起来
li.extend(buc)
return li
import random
li = [random.randint(0,10000) for i in range(100000)] # 创建一个0-10000的随机数列表
li = BucketSort(li)
print(li) 排序结果如图:

桶排序改进:
从代码中可以看出在每个数插入到桶中时,要对该数在通中的顺序进行排序调整,用的是插入排序进行比较来使桶序列有序的,这种方法还是比较慢的,我们可以使用其他的排序方法来代替插入排序。如快速排序。
代码实现:
由于我们用到快速排序,我们可以把我们之前写的快速排序进行一下改装,放到QuickSort.py下
之前的快速排序代码:
def partition(li, left, right):
tmp = li[left] # 设置tmp为最左边起始值
while left < right:
while left < right and li[right] >= tmp: # 从右边找比tmp小的数
right -= 1 # 没找到就往左走一步
li[left] = li[right] # 找到了比tmp小的,就把右边的值写到左边空位上,否则就是left=right
while left < right and li[left] <= tmp: # 从左边找比tmp大的数
left += 1 # 没找到就往右走一步
li[right] = li[left] # 找到了比tmp大的,就把左边的值写到右边空位上,否则就是left=right
li[left] = tmp # 此时,right=left为空,把tmp值放置到此处,
return left # 返回下标,对左右两边进行递归排序
def QuickSort(li, left, right):
if left < right: # 至少两个元素,一个不需要
mid = partition(li, left, right) # 排序并返回mid(相对)
QuickSort(li, left, mid - 1) # 对mid左边排序
QuickSort(li, mid + 1, right) # 对mid右边排序我们为了比较一下改进是否有效,比较其排序时间更直观。因此我们需要一个装饰器。来记录每个函数的排序时间。
装饰器代码如下:
import time
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print("%s 运行时间: %s secs." %(func.__name__, t2-t1))
return result
return wrapper改进版桶排序及比较:
import copy
import random
import sys
from cal_time import *
import QuickSort
# 原版桶排序
@cal_time
def BucketSort(li, n=100, max_num=10000):
buckets = [[] for _ in range(n)] # 创建桶
for var in li:
i = min(var // (max_num // n), n-1) # i 表示var放到几号桶里,最后一个桶是最大的一段数
buckets[i].append(var) # 把var加到对应的桶里面
# 保持桶内的顺序
for j in range(len(buckets[i])-1, 0, -1):
if buckets[i][j] < buckets[i][j-1]:
buckets[i][j], buckets[i][j-1] = buckets[i][j-1], buckets[i][j]
else:
break
li.clear()
for buc in buckets: # 每个桶内都是有序的,连接起来
li.extend(buc)
return li
# 改进版
@cal_time
def BucketSortPro(li, n=100, max_num=10000):
buckets = [[] for _ in range(n)] # 创建桶
for var in li:
i = min(var // (max_num // n), n-1) # i 表示var放到几号桶里,最后一个桶是最大的一段数
buckets[i].append(var) # 把var加到对应的桶里面
# 保持桶内的顺序, 使用快排进行每个桶的排序
for i in buckets:
QuickSort.QuickSort(i,0,len(i)-1)
li.clear()
for buc in buckets: # 每个桶内都是有序的,连接起来
li.extend(buc)
return li
# 快速排序
@cal_time
def quicksort(li):
"""
:type li: list
"""
QuickSort.QuickSort(li,0,len(li)-1)
return li
li = [random.randint(0,10000) for i in range(100000)] # 创建范围很大的随机序列
li1 = copy.deepcopy(li) # 将序列深拷贝3份
li2 = copy.deepcopy(li)
li3 = copy.deepcopy(li)
li1 = BucketSort(li1)
li2 = BucketSortPro(li2)
li3 = quicksort(li3) # 排序结果是一样的,我们看排序时间快慢运行时间比较:
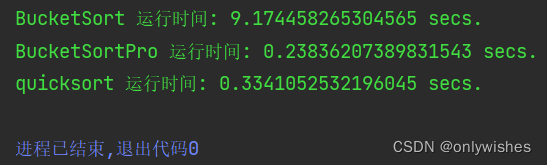
可以看到改进前桶排序用时达到了9秒多, 而快速排序用时0.3341秒,明显快排较快,而改进后的桶排序内部也采用了快速排序,结果比快排还要快为0.2383秒,所以改进是有效的且显著的。



![[ChatGPT]](https://img-blog.csdnimg.cn/img_convert/a646c6fec3634300acb88545051acb68.jpeg)