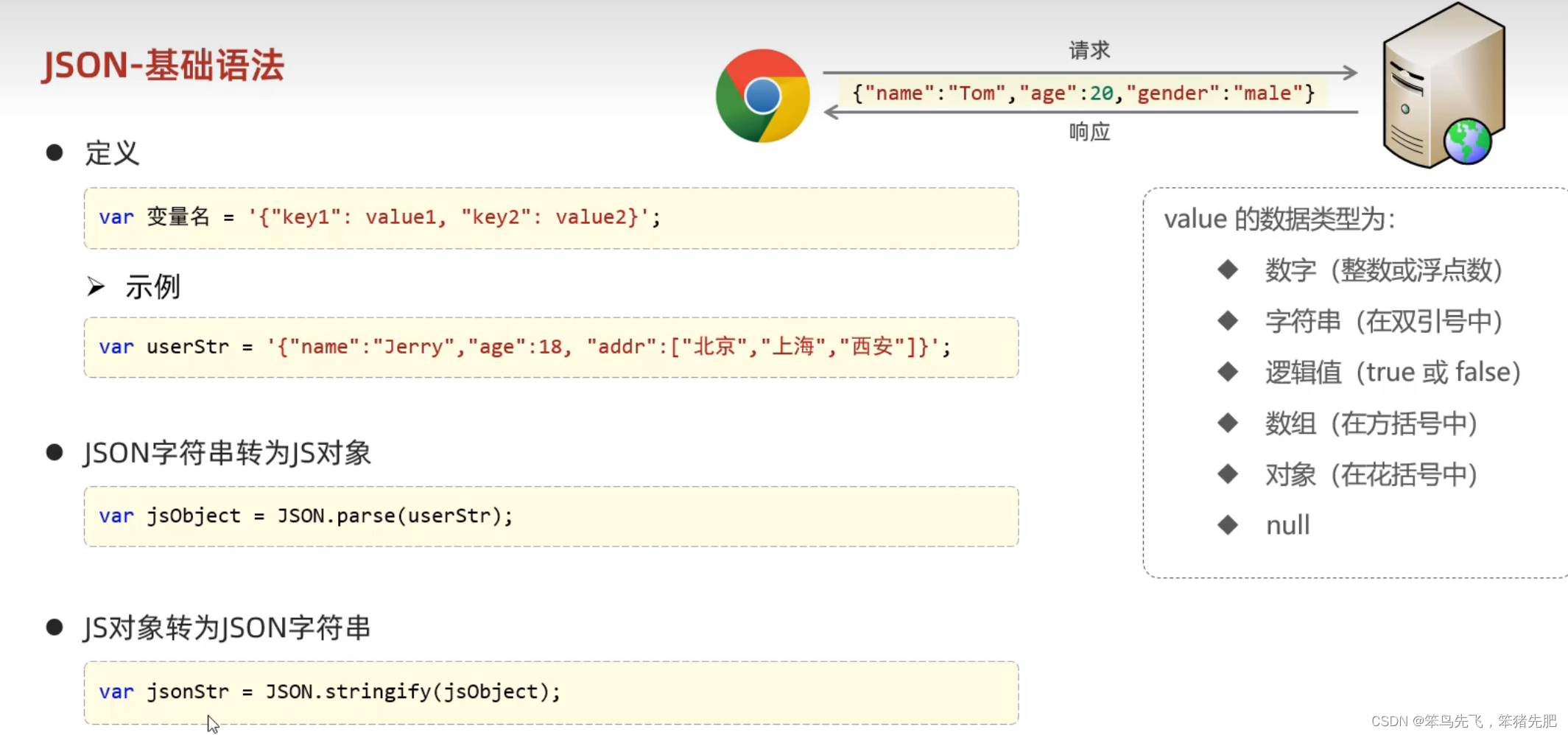
1.整数拆分

代码随想录

视频讲解：动态规划，本题关键在于理解递推公式！| LeetCode：343. 整数拆分_哔哩哔哩_bilibili

代码：

class Solution {
public:
    int integerBreak(int n) {
        // dp[i] 拆分数字i所获得的最大乘积为dp[i]
        vector<int> dp(n + 1,0);
        // 初始化
        dp[2] = 1;
        // 递推公式
        for(int i = 3;i <= n; i++){
            for(int j = 1;j < i - 1; j++){
                dp[i] =max(dp[i], max(j * (i - j),j * dp[i - j]));
            }
        }
        return dp[n];
    }
};

 思路：

dp数组的含义：拆分数字i所获得的最大乘积为dp[i]

dp数组的递推公式：分为两种情况，拆分为两个数字，拆分为两个以上的数字。因此，dp[i] =max(dp[i], max(j * (i - j),j * dp[i - j]))。

        这里要强调的是：max函数里dp[i]是为了去记录 之前遍历j的不同数值时的 等号左边的最终要求得的dp[i] 可能取到的最大值——通过不断更新 dp[i] 的值，我们可以在动态规划的过程中找到拆分数字 i 所获得的最大乘积。也正是因为这种记录历史信息的方式，我们才能够不断地比较并选择最优解，从而得到最终的结果。

dp数组的初始化：从dp[2]开始有意义，dp[2]初始化为1

遍历顺序：从左到右

2.不同的二叉搜索树 

代码随想录

视频讲解：动态规划找到子状态之间的关系很重要！| LeetCode：96.不同的二叉搜索树_哔哩哔哩_bilibili

代码：

class Solution {
public:
    int numTrees(int n) {
        // dp[i]表示i个节点组成的互不相同的二叉搜索树的种类
        vector<int> dp(n + 1,0);
        // 初始化
        dp[0] = 1;
        // 递推公式
        for(int i = 1; i <= n; i++){
            for(int j = 1;j <= i ;j++){
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};

 思路：

dp数组的含义：dp[i]表示i个节点组成的互不相同的二叉搜索树的种类

dp数组的递推公式：确认好一个节点为根结点，dp[i]就等于 它的不同数目左右子树的种类和的乘积 的总和。即dp[i] += dp[j - 1] * dp[i - j]

dp数组的初始化：

从递归公式上来讲，dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0，也需要dp[以j为头结点左子树节点数量] = 1， 否则乘法的结果就都变成0了。

因此dp[0] = 1

遍历顺序：从左到右 

我在做这道题的时候，犯了两个错，一个是我忘记左右子树的节点总数是i-1了，另一个是dp[i]对应着不同数目的左右子树，因此它是取不同情况的总和数。