本周有一个客户,购买Hostease的虚拟主机,询问我们的在线客服,如何在.htaccess文件创建一个自定义404页面?我们为用户提供相关教程,用户很快解决了遇到的问题。在此,我们分享这个操作教程,希望可以对您有帮助。
自定义 404 页面发挥作用,它允许网站所有者为登陆到丢失页面的访问者创建更友好、更吸引人的体验。修改 .htaccess 文件的最简单方法是使用 cPanel 的文件管理器,并按照下面的说明操作,当然也可以通过 FTP 上传 .htaccess 文件。
第一步:登入到用户cPanel面板。
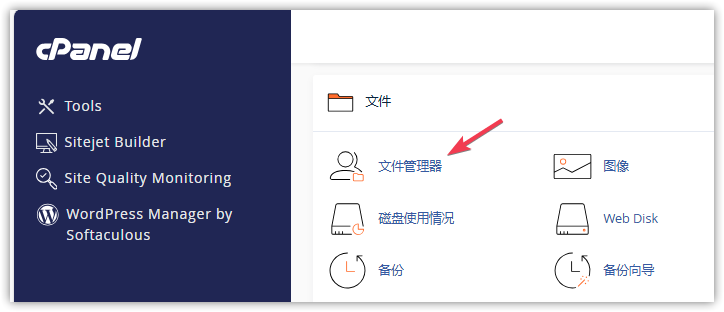
第二步:在 "文件 "部分点击 "文件管理器"。
第三步:导航至网站的文档根文件夹。
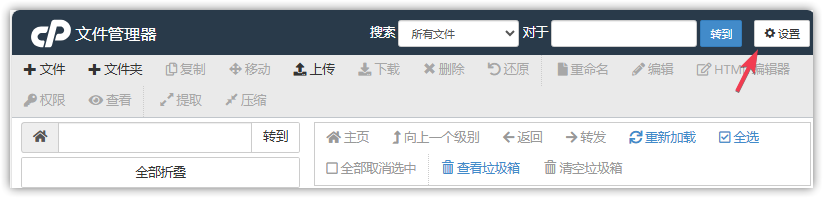
第四步:点击设置。
第五步:确保选择了显示隐藏文件。

第六步:右键单击 .htaccess 文件并选择编辑。
如果您已经有了一个静态 HTML 页面,希望用于处理 404 错误,也可以直接用 .htaccess 文件指向该文件。在本例中,我们要提供一个 404.html 页面。请务必将 "404.html "替换为实际页面名称:

编辑完 .htaccess 文件后,点击保存更改。
到此,在.htaccess文件创建一个自定义404页面操作就完成了!