一、二分查找基础
(1)int mid = ((right - left) >> 1) + left;
(2)lower_bound的底层实现
int lower_bound(vector<int>& nums, int x)
{
int left = 0;
int right = nums.size() - 1;
// 区间为 左闭右闭
while (left <= right) {
int mid = left +(right - left) / 2;
if (x > nums[mid]) {
left = mid + 1;
}
else {
right = mid - 1;
}
}
return left;
}
upper_bound用法和上面类似。只是把lower_bound的 【大于等于】 换成 【大于】 。仿函数等等全是相同的用法
底层实现
int upper_bound(vector<int>& nums, int x) {
int left = 0;
int right = nums.size() - 1;
while (left <= right) {
int mid = left +(right - left) / 2;
if (x >= nums[mid]) { //这里是大于等于
left = mid + 1;
}
else {
right = mid - 1;
}
}
return left;
}
(3)binary_search()实现
template <class ForwardIterator, class T>
bool binary_search (ForwardIterator first, ForwardIterator last, const T& val)
{
first = std::lower_bound(first,last,val);
return (first!=last && !(val<*first));
}
(5)二分查找
int search(vector<int>& nums, int target){
// 二分查找区间[left, right),初始为整个区间
int left = 0;
int right = nums.size();
// 找到首个大于target的值
while(left < right){
int mid = left + ((right - left) >> 1);
if(nums[mid] > target){
right = mid; // 找到一个大于target的值,暂存并在左半区间继续查找
}else{
left = mid + 1; // 没有找到大于target的值,在右半区间继续查找
}
}
return right;
}
二、35. 搜索插入位置
1 题目

2 解题思路
(1)由于是排序数组,所以可以使用二分法来进行目标值查找
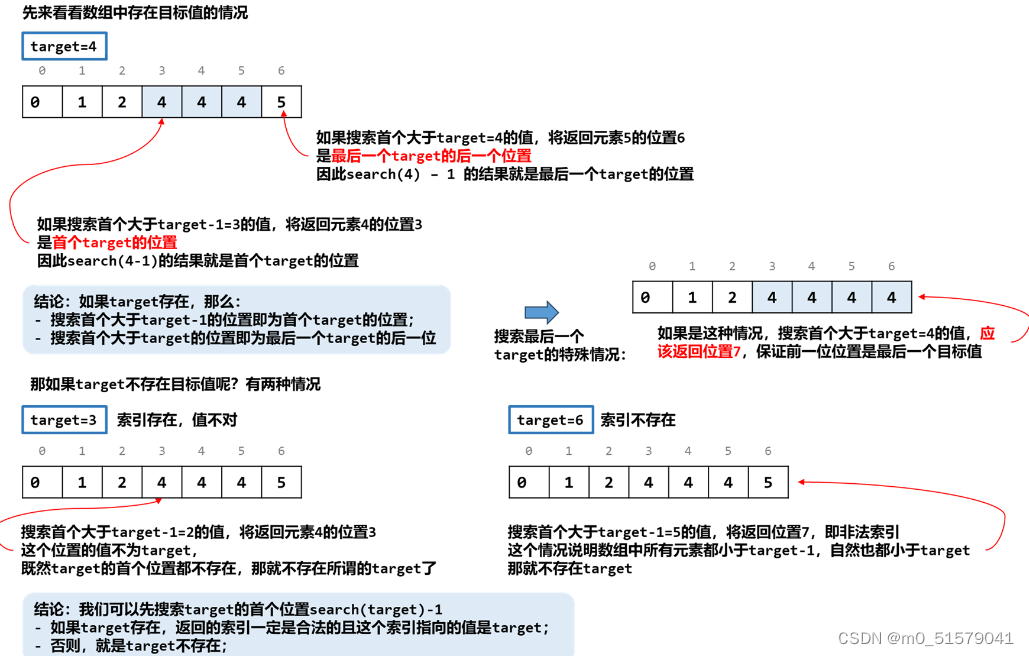
(2)假设题意是叫你在排序数组中寻找是否存在一个目标值,那么训练有素的读者肯定立马就能想到利用二分法在 O(logn)的时间内找到是否存在目标值。但这题还多了个额外的条件,即如果不存在数组中的时候需要返回按顺序插入的位置,那我们还能用二分法么?答案是可以的,我们只需要稍作修改即可。
考虑这个插入的位置 pos,它成立的条件为:
nums[pos−1]<target≤nums[pos]
其中 nums 代表排序数组。由于如果存在这个目标值,我们返回的索引也是 pos,因此我们可以将两个条件合并得出最后的目标:「在一个有序数组中找第一个大于等于 target的下标」。
问题转化到这里,直接套用二分法即可,即不断用二分法逼近查找第一个大于等于 target的下标 。下文给出的代码是笔者习惯的二分写法,ans 初值设置为数组长度可以省略边界条件的判断,因为存在一种情况是 target 大于数组中的所有数,此时需要插入到数组长度的位置。
3 code
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int n=nums.size();
int left=0;
int right=n-1;
int ans=n;
while(left<=right)
{
// >>1相当于/2
int mid= left+((right-left)>>1);
//移动逻辑
if(target<=nums[mid])
{
ans=mid;
right=mid-1;
}
else
{
left=mid+1;
}
}
return ans;
}
};
三、74. 搜索二维矩阵
1 题目

2 解题思路
(1)由于每行的第一个元素大于前一行的最后一个元素,且每行元素是升序的,所以每行的第一个元素大于前一行的第一个元素,因此矩阵第一列的元素是升序的。
(2)我们可以对矩阵的第一列的元素二分查找,找到最后一个不大于目标值的元素,然后在该元素所在行中二分查找目标值是否存在。
3 code
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target)
{
// 我们可以对矩阵的第一列的元素二分查找,找到最后一个不大于目标值的元素
auto row=upper_bound(matrix.begin(),matrix.end(),target,[](const int b, const vector<int>&a)
{
return b<a[0];
});
if(row==matrix.begin())
{
return false;
}
--row;
//然后在该元素所在行中二分查找目标值是否存在。
return binary_search(row->begin(),row->end(),target);
}
};
四、34. 在排序数组中查找元素的第一个和最后一个位置
1 题目

2 解题思路
3 code
class Solution {
private:
/**
* @brief 返回首个大于target的元素索引,如果不存在,返回数组长度n
* @param nums: 输入数组
* @param target: 目标值
* @return: 目标值索引
*/
int search(vector<int>& nums, int target){
// 二分查找区间[left, right),初始为整个区间
int left = 0;
int right = nums.size();
// 找到首个大于target的值
while(left < right){
int mid = left + ((right - left) >> 1);
if(nums[mid] > target){
right = mid; // 找到一个大于target的值,暂存并在左半区间继续查找
}else{
left = mid + 1; // 没有找到大于target的值,在右半区间继续查找
}
}
return right;
}
public:
vector<int> searchRange(vector<int>& nums, int target) {
// 首个target如果存在,一定是首个大于target-1的元素
int start = search(nums, target - 1);
if(start == nums.size() || nums[start] != target){
return {-1, -1}; // 首个target不存在,即数组中不包含target
}
// 找到首个大于target的元素,最后一个target一定是其前一位
int end = search(nums, target);
return {start, end - 1};
}
};
五、34. 在排序数组中查找元素的第一个和最后一个位置
1 题目

2 解题思路
这道题要在一个旋转了的有序数组中搜索目标值,要求时间复杂度为 O(logn)。这个时间复杂度只能首先尝试二分查找,但是二分查找的前提是数组有序,这个数组并不满足,还可以用吗?
先别急,虽然这个数组不是整体有序,但它是局部有序的,我们尝试二分着去做看看会发生什么。
二分每次都需要取中点 mid,对于这个旋转的有序数组:
- 如果当前区间 [left, right) 分别在两端有序区间之内,那么就按二分查找去做即可。
- 如果当前区间 [left, right) 是跨越了两端有序子区间的,那么中间点 mid 总会把当前区间 [left, right] 分成两段,一段是有序的,一段是无序的:
(1)如果 nums[mid] > nums[left],肯定是左半区间有序;
(2)如果 nums[mid] < nums[right-1],肯定是右半区间有序;【之所以 -1,是因为 right 初始为数组长度 n,直接取 right 会导致越界】
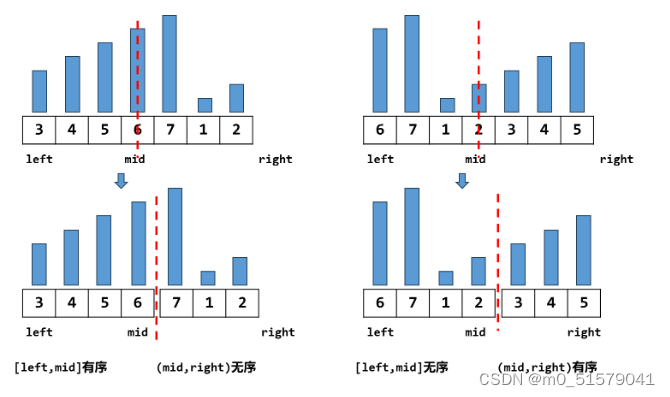
二分的策略还是一样的,二分的关键是要判断 target 落在哪个区间。我们只能取有序的那个区间来比较,因为只有区间有序,才能 通过端点值的大小比较判断是否落入对应的区间

因此我们只要能够每次判断目标值落到哪个区间,就可以通过二分排除另一半的区间,并不一定要求必须整个数组有序。

3 code
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0; // 二分查找左边界(左闭)
int right = nums.size(); // 二分查找右边界(右开)
while(left < right){
int mid = left + ((right - left) >> 1);
if(nums[mid] == target){
// 找到目标值,直接返回索引
return mid;
}
if(nums[left] < nums[mid]){
// 左半区间有序
if(nums[left] <= target && target < nums[mid]){
right = mid; // 目标值落入左半区间,更新右边界
}else{
left = mid + 1; // 否则在右半区间查找
}
}else{
// 右半区间有序
if(nums[mid] < target && target <= nums[right -1]){
left = mid + 1; // 目标值落入右半区间,更新左边界
}else{
right = mid; // 否则在左半区间查找
}
}
}
return -1; // 如果退出循环,说明没有找到目标值,返回-1
}
};
六、153. 寻找旋转排序数组中的最小值
1 题目