更好的阅读体验

Skiers

Description

给定 $n$ 个点的有向无环平面图，求最少多少条从 $1$ 到 $n$ 的路径能覆盖原图的所有边？

$1\le n\le 5\times 10^3$

Solution

考虑从 $1$ 到 $n$ 的路径其实是边的链覆盖，那么最小链覆盖即为求解的答案。通过 Dilworth 定理可知，最小链覆盖等于最大反链，从而问题转化为求最大反链（两两无法到达的边的集合）。

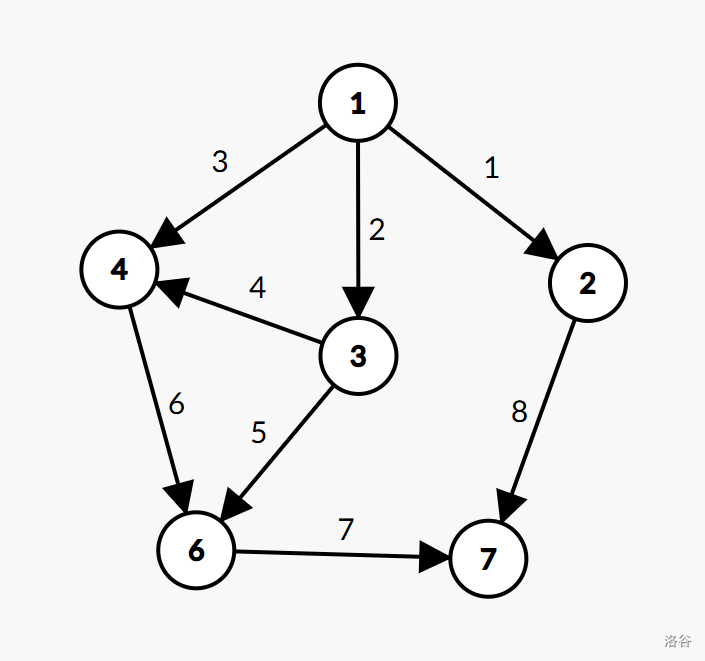
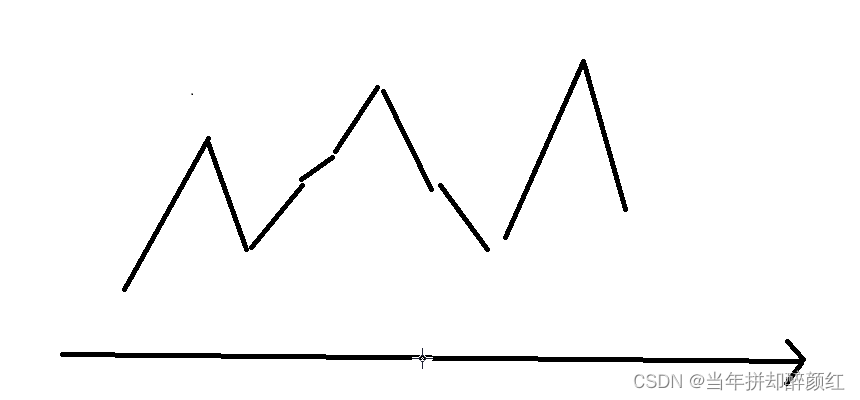
例如：图示的有向无环平面图，$1$ 号点为起点，$7$ 号点为汇点。最大反链是 $3,4,5,8$ 边构成的集合（注意集合不唯一），不难发现原图的答案就是 $4$。

考虑如何求解最大反链，可以将平面图转化为对偶图，则最大反链即为对偶图的最长路。

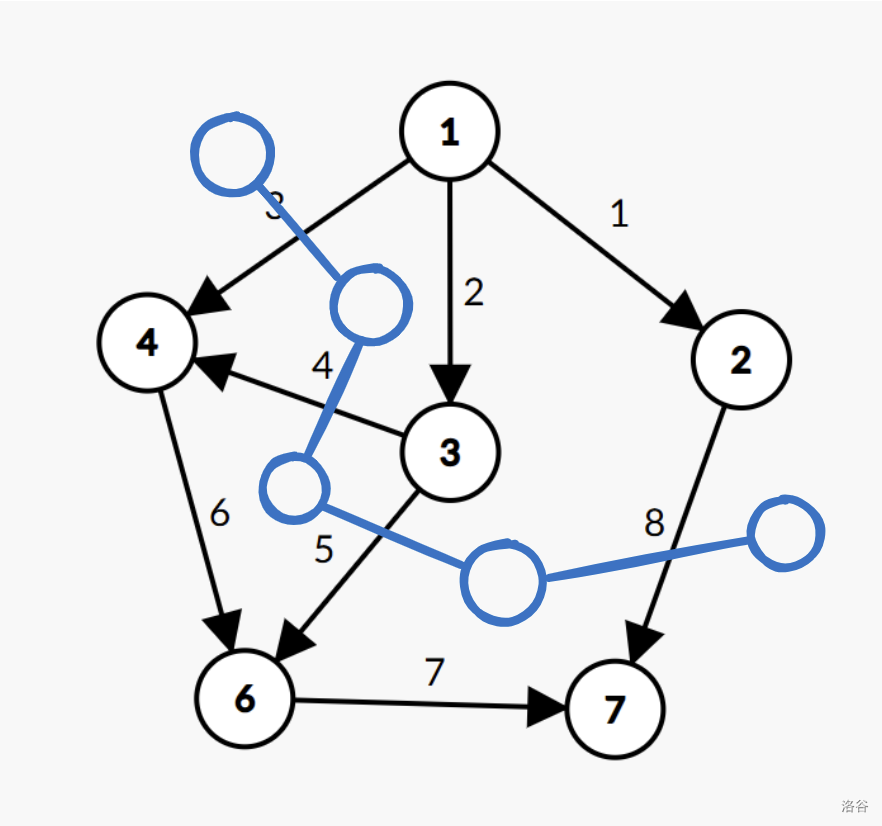
如图，给出了原图的对偶图的最长路，注意这里多开了虚拟起点和汇点。

那么，怎么求最长路呢，这里给出一种简单又迅速的做法，从起点开始 DFS，如果遍历到 $1$ 个点之前已经遍历过了，那么说明多出了一条对偶图的边。

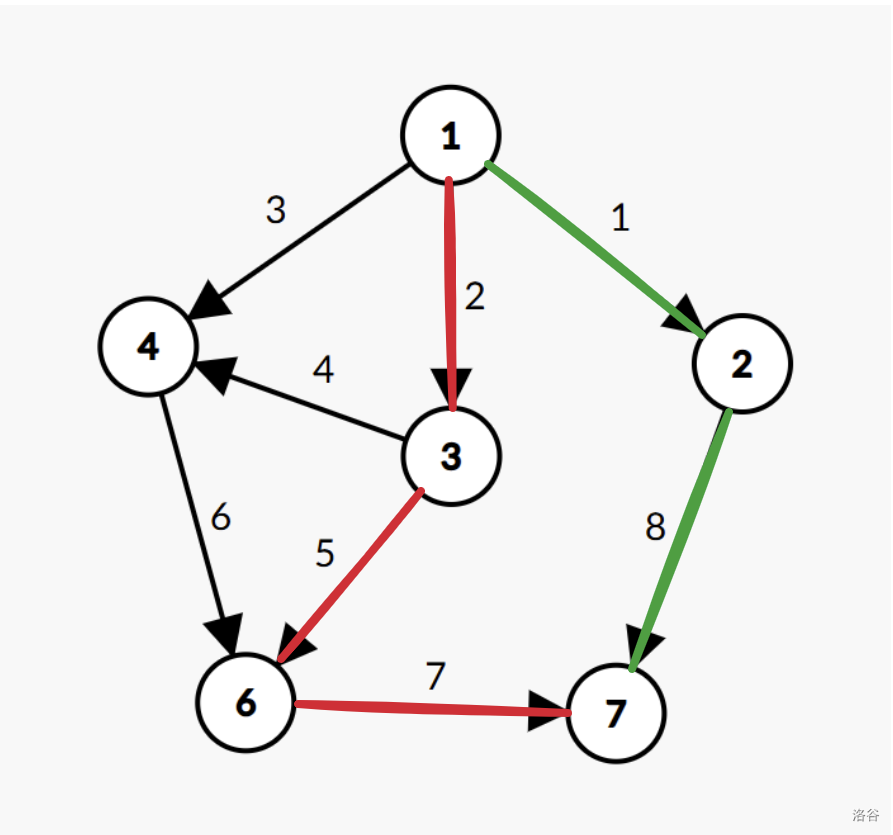
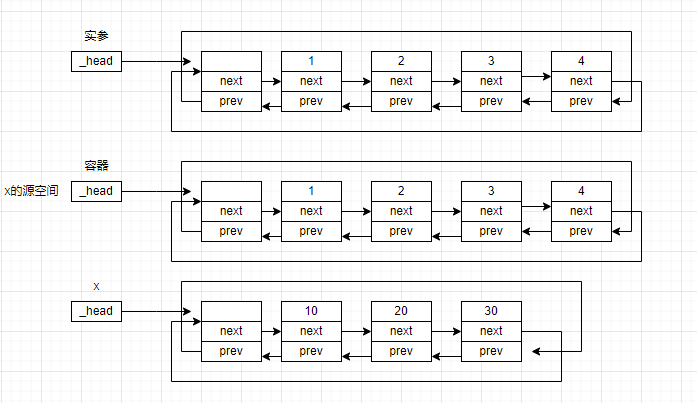
若绿色路径为当前 DFS 的路径，红色为之前 DFS 的路径，此时发现到达了一个已经经过的点，则从该点开始将红色的边筛出来，直到绿色节点经过过的点，即 $1$ 号节点。用红色边最长路 $+1$ 再去更新绿色边的最长路即可。

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 5e3 + 10, M = 3 * N;

int n;
int h[N], e[M], ne[M], idx;
int st[N], dp[M];
PII lst[N];

void add(int a, int b) {
	e[idx] = b, ne[idx] = h[a], dp[idx] = 1, h[a] = idx ++;
}
void dfs(int u) {
	st[u] = 1;
	for (int i = h[u]; ~i; i = ne[i]) {
		int v = e[i];
		if (st[v] == 0) lst[v] = {u, i}, dfs(v);
		else {
			int res = 0, tmp = u;
			while (st[v] == -1) res = max(res, dp[lst[v].se] + 1), v = lst[v].fi;
			dp[i] = res;
			while (tmp != v) dp[lst[tmp].se] = res, tmp = lst[tmp].fi;
			lst[e[i]] = {u, i};
		}
	}
	st[u] = -1;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> n;
	memset(h, -1, sizeof h);

	int k, x;
	for (int i = 1; i < n; i ++) {
		cin >> k;
		for (int j = 1; j <= k; j ++)
			cin >> x, add(i, x);
	}

	dfs(1);

	int res = 0;
	for (int i = 0; i < idx; i ++)
		res = max(res, dp[i]);

	cout << res << endl;

	return 0;
}