力扣爆刷第146天之贪心算法五连刷
文章目录
- 力扣爆刷第146天之贪心算法五连刷
- 总结
- 一、455. 分发饼干
- 二、376. 摆动序列
- 三、53. 最大子数组和
- 四、122. 买卖股票的最佳时机 II
- 五、5. 跳跃游戏
总结
贪心算法的本质就是选择每一阶段的局部最优,从而达到全局最优。
一、455. 分发饼干
题目链接:https://leetcode.cn/problems/assign-cookies/description/
思路:求满足最多的饼干数量,即每个孩子需要吃的数量必须被饼干覆盖,要想达到最多,只需要给孩子和饼干分别排序,然后逐个比较大小,满足需求即计数。
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int count = 0, i = 0, j = 0;
while(i < g.length && j < s.length) {
if(g[i] <= s[j]) {
count++;
i++;
}
j++;
}
return count;
}
}
二、376. 摆动序列
题目链接:https://leetcode.cn/problems/wiggle-subsequence/description/
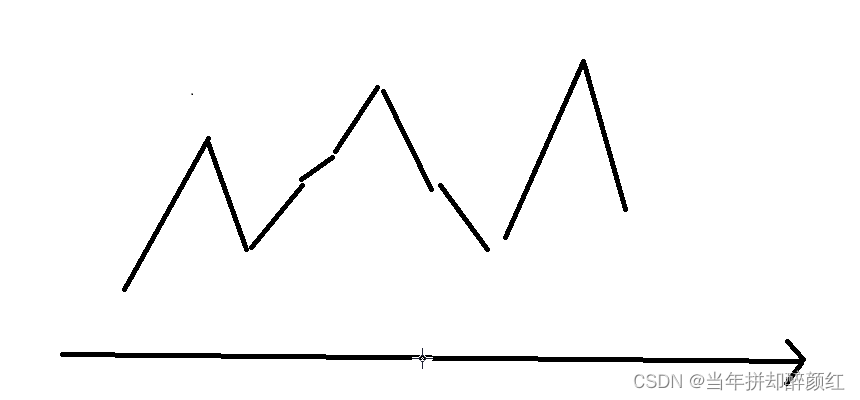
思路:求最长摆动序列,可以发现,本题是可能出现相邻状态一致的情况,简化来看,就是需要从头到尾比较相邻元素差的正负情况,如果差的情况一样,跳过即可,这样剩下的就都是相邻差不一致的了,只不过启动需要做一下处理。
下图为: true、false、true、true、true、false、false、true、false,只需要跳过相邻一致的情况,即可。
class Solution {
public int wiggleMaxLength(int[] nums) {
if(nums.length == 1) return 1;
int count = 1;
boolean flag = true, pro = false;
for(int i = 1; i < nums.length; i++) {
if(nums[i] == nums[i-1]) continue;
boolean cur = nums[i] - nums[i-1] > 0;
if(flag) {
pro = !cur;
flag = false;
}
if(pro != cur) {
count++;
pro = cur;
}
}
return count;
}
}
三、53. 最大子数组和
题目链接:https://leetcode.cn/problems/maximum-subarray/description/
思路:求最大子数组和,是连续子数组,可以使用动态规划,也可以使用贪心,下面分别展示。
动态规划:定义dp[i]表示以nums[i]为结尾的最大子数组和,既然是以nums[i]为结尾,那么要求累加和必须要大于nums[i],如果小于nums[i]则直接以nums[i]为起点,也是结尾,新开累加计算。
贪心是类似,基本思路就是记录累加和,但只要当前值小于0就重新计算。
class Solution {
public int maxSubArray(int[] nums) {
int max = nums[0], sum = nums[0];
for(int i = 1; i < nums.length; i++) {
sum = Math.max(sum + nums[i], nums[i]);
max = Math.max(max, sum);
}
return max;
}
}
贪心:
class Solution {
public int maxSubArray(int[] nums) {
int max = Integer.MIN_VALUE, sum = 0;
for(int i = 0; i < nums.length; i++) {
sum += nums[i];
if(sum > max) max = sum;
if(sum < 0) sum = 0;
}
return max;
}
}
四、122. 买卖股票的最佳时机 II
题目链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/description/
思路:本题可以使用动态规划也可以使用贪心。
动态规划:定义每一天有两种状态,即持有与不持有,如果持有分为当天持有和之前就已经持有,如果不持有分为当天就不持有和之前就已经不持有。然后根据状态进行选择。
class Solution {
public int maxProfit(int[] prices) {
int[] dp = new int[2];
dp[0] = -prices[0];
for(int i = 1; i < prices.length; i++) {
dp[0] = Math.max(dp[0], dp[1]-prices[i]);
dp[1] = Math.max(dp[1], dp[0]+prices[i]);
}
return dp[1];
}
}
贪心:因为买卖股票是相邻两天的差值,那为了利益最大化,自然是只要差值大于0就累加,差值小于0就不加,即不交易。
class Solution {
public int maxProfit(int[] prices) {
if(prices.length == 1) return 0;
int sum = 0;
for(int i = 1; i < prices.length; i++) {
int t = prices[i] - prices[i-1];
if(t > 0) {
sum += t;
}
}
return sum;
}
}
五、5. 跳跃游戏
题目链接:https://leetcode.cn/problems/jump-game/description/
思路:跳跃游戏,其实就是一个右边界的扩大过程,如果向右行进超过了右边界即无法跳跃,如果一直为于右边界内,且遍历结束,右边界大于数组结尾,即可以跳跃成功。
class Solution {
public boolean canJump(int[] nums) {
if(nums.length == 1) return true;
int right = nums[0];
for(int i = 1; i < nums.length; i++) {
if(i > right) return false;
if(nums[i] + i > right) right = nums[i] + i;
}
return true;
}
}