🎩 欢迎来到技术探索的奇幻世界👨‍💻

📜 个人主页：@一伦明悦-CSDN博客

✍🏻 作者简介： C++软件开发、Python机器学习爱好者

🗣️ 互动与支持：💬评论      👍🏻点赞      📂收藏     👀关注+

如果文章有所帮助，欢迎留下您宝贵的评论，

点赞加收藏支持我，点击关注，一起进步！

目录

前言             

正文 

01-k近邻简介           

02-最近邻回归实战           

03-基于局部离群因子算法进行离群检测          

 04-最近邻分类实战         

05-最近邻质心分类实战         

总结             

---

前言             

       sklearn.neighbors是scikit-learn库中用于实现K近邻算法的模块。它提供了用于分类、回归、密度估计等任务的K近邻算法的实现。该模块包含了多种K近邻算法的实现，如基本的KNN分类器、回归器、最近邻图等。你可以使用该模块来构建K近邻模型，并对数据进行分类、回归等任务。

        K近邻（K-Nearest Neighbors，KNN）是一种常用的监督学习算法，用于分类和回归问题。在分类问题中，给定一个未标记的样本，KNN算法会通过查找其最近的K个已标记的样本（即邻居），以多数投票的方式确定该样本的类别。在回归问题中，KNN算法会通过取其K个最近邻居的平均值来预测目标变量的值。KNN算法的核心思想是假设相似的样本在特征空间中具有相似的类别或值。

        接下来，本篇内容将从k近邻算法原理出发，逐步介绍k近邻的用法，并给出具体代码分析应用过程。

正文 

01-k近邻简介           

        K近邻算法（K-Nearest Neighbors，KNN）是一种基本的监督学习算法。其原理简单而直观：给定一个未标记的样本，通过计算其与训练集中所有已标记样本的距离，找到离该样本最近的K个邻居（即最相似的K个样本），然后利用这K个邻居的标记信息进行决策。

计算过程可以简述为：

         计算未标记样本与训练集中每个已标记样本的距离，常用的距离度量包括欧氏距离、曼哈顿距离等。

        根据距离找出K个最近邻居。        

        对于分类问题，采用多数投票的方式确定未标记样本的类别，即将K个最近邻居中出现次数最多的类别作为未标记样本的预测类别。

        对于回归问题，采用平均值或加权平均值的方式确定未标记样本的目标值 

        现在我们来看一个K近邻分类的例子，并通过可视化代码来分析应用过程。让我们假设我们有一个简单的二维数据集，包含两个类别，我们想要使用KNN算法对其进行分类。我们将使用Python的matplotlib和scikit-learn库来实现这个例子。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.neighbors import KNeighborsClassifier

# 生成一个二维数据集
X, y = make_classification(n_samples=100, n_features=2, n_informative=1, n_redundant=0, n_repeated=0, n_classes=2, n_clusters_per_class=1, random_state=42)

# 创建KNN分类器
knn = KNeighborsClassifier(n_neighbors=3)

# 拟合模型
knn.fit(X, y)

# 可视化数据集
plt.figure(figsize=(8, 6))

# 绘制样本点
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, marker='o', s=50)

# 绘制决策边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])

# 将结果放入彩色图中
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)

plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('KNN Classification')

plt.show()

        示例运行结果如下图所示：

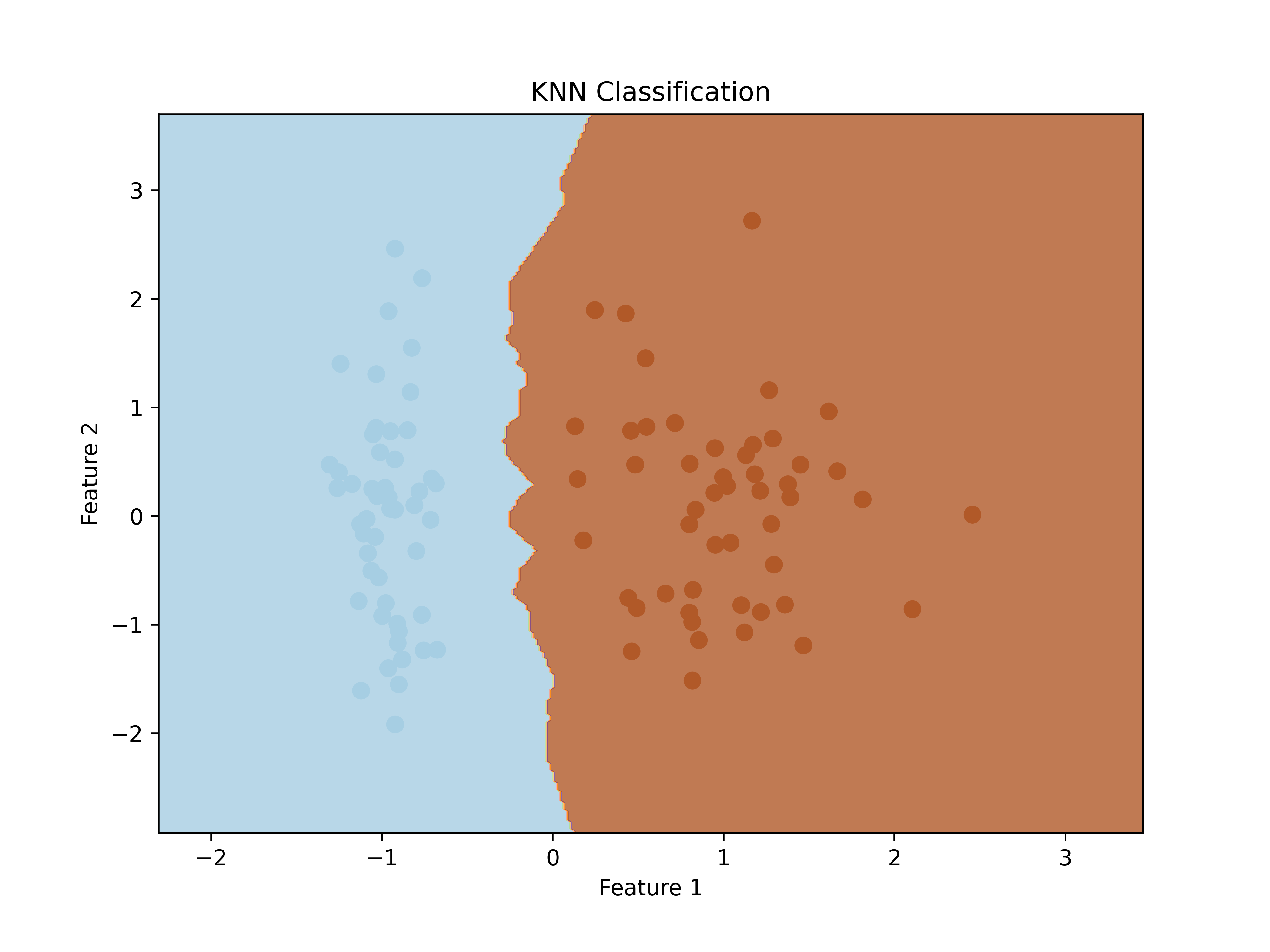
02-最近邻回归实战           

        在K近邻算法中，除了可以用于分类问题外，也可以用于回归问题。对于回归问题，KNN算法的原理与分类问题类似，但是在确定未标记样本的目标值时，不再使用多数投票的方式，而是采用平均值或加权平均值的方式。

        具体来说，对于每个未标记样本，找到其K个最近邻居后，可以使用以下两种方法来确定其目标值：

        平均值：简单地将K个最近邻居的目标值取平均作为未标记样本的预测目标值。

        加权平均值：根据距离远近，对K个最近邻居的目标值进行加权平均。通常距离越近的样本权重越大，距离越远的样本权重越小，可以使用距离的倒数或其他加权方式来计算权重。

        在回归问题中，使用K近邻算法可以实现非常灵活的插值方法，因为它不依赖于数据的分布假设，而是直接根据数据的局部结构进行预测。这使得KNN算法在处理非线性、非参数化的回归问题时具有一定的优势。

        在实际应用中，可以根据数据的特点和需求选择合适的K值、距离度量方法以及加权方式，来调整K近邻算法的表现，以达到最佳的回归效果。

        下面给出一个代码示例分析应用过程：这段代码演示了使用K近邻算法进行回归的示例。示例分析如下：

        通过np.random.seed(0)设置随机种子，然后生成一组带有噪声的正弦波数据作为样本数据X和y。

        创建一组用于预测的数据T，这里是在0到5之间均匀分布的500个数据点。

        在原始正弦波数据y中每隔5个样本添加随机噪音，模拟真实世界中的数据。

        确定K值为5，在两种不同的权重计算方式下（uniform和distance），分别拟合K近邻回归模型并进行预测。

# 获得样本数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn import neighbors
plt.rcParams['font.sans-serif'] = ['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus'] = False 

np.random.seed(0)
X = np.sort(5 * np.random.rand(40, 1), axis=0)
T = np.linspace(0, 5, 500)[:, np.newaxis]
y = np.sin(X).ravel()

# 在标签中添加噪音
y[::5] += 1 * (0.5 - np.random.rand(8))

# #############################################################################
# 拟合回归模型
n_neighbors = 5

for i, weights in enumerate(['uniform', 'distance']):
    knn = neighbors.KNeighborsRegressor(n_neighbors, weights=weights)
    y_ = knn.fit(X, y).predict(T)

    plt.subplot(2, 1, i + 1)
    plt.scatter(X, y, color='red', label='数据')
    plt.plot(T, y_, color='blue', label='预测')
    plt.axis('tight')
    plt.legend()
    plt.title("k近邻回归 (k = %i, weights = '%s')" % (n_neighbors,weights))

plt.tight_layout()
plt.savefig("../4.png", dpi=500)
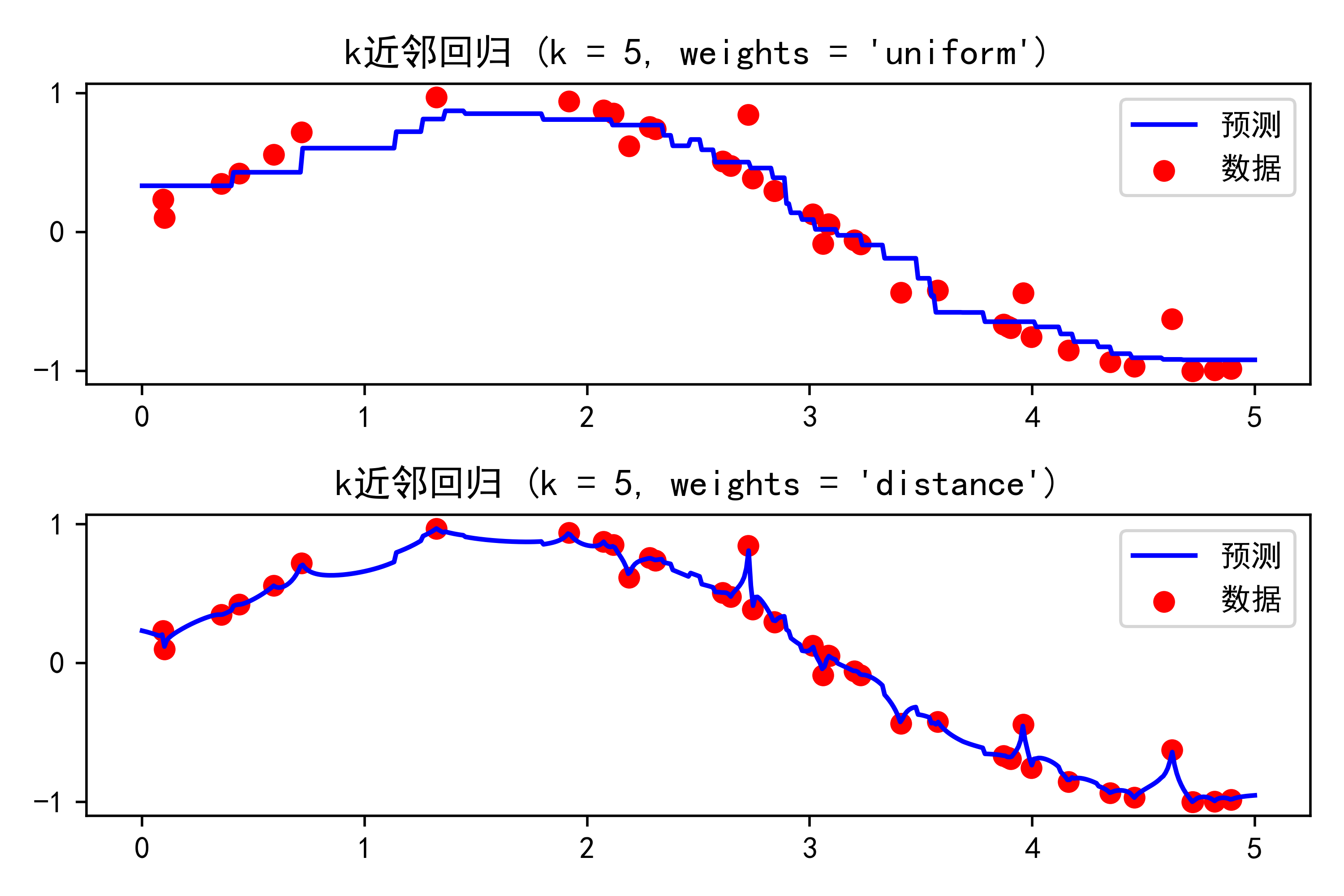
plt.show()

        示例运行结果如下图所示：

        上半部分展示了基于uniform权重计算方式的K近邻回归结果。红色点表示原始数据样本，蓝色线为模型预测的回归曲线。

        下半部分展示了基于distance权重计算方式的K近邻回归结果，同样红色点代表原始数据样本，蓝色线为模型预测的回归曲线。

        通过这两幅图可以清晰地看到，K近邻回归模型在样本数据点附近对数据的趋势进行了不错的拟合，尤其是在添加噪音的情况下，模型依然能够较好地捕捉到数据的整体趋势。

03-基于局部离群因子算法进行离群检测          

        局部离群因子算法（LOF）是一种常用的离群检测方法，用于识别数据集中的离群点或异常点。它与传统的离群检测方法相比，更加注重数据点与其邻近点之间的关系，而不是全局的统计特征。

        具体来说，LOF算法通过计算每个数据点周围邻近点的密度来度量其离群程度。一个数据点的局部离群因子（LOF）值表示该点与其邻近点的密度相比较于邻近点的密度之比，从而反映了该点的异常程度。如果一个点的LOF值远高于其邻近点的平均密度，那么它很可能是一个离群点。

        LOF算法的主要步骤包括：

        对于每个数据点，计算其到其K个最近邻点的距离，这些距离可以用来估计该点的密度。

        计算每个数据点的局部可达密度（Local Reachability Density，LRD），表示该点相对于其邻近点的密度。

        计算每个数据点的局部离群因子（LOF），表示该点相对于其邻近点的异常程度。

        根据计算出的LOF值对数据点进行排序，找出离群点。

        LOF算法的优点是能够有效地识别非球形和高维数据中的离群点，且不需要对数据的分布做出假设。然而，它也有一些缺点，例如对参数K的选择比较敏感，且计算复杂度较高。

        总的来说，LOF算法是一种强大的离群检测方法，适用于各种类型的数据集和应用场景，能够帮助用户发现潜在的异常情况和问题。

        下面给出一个具体的代码示例分析应用过程：这段代码演示了使用局部离群因子算法（LOF）进行离群检测的示例。详细分析如下：

        首先，使用np.random.seed(42)设置随机种子，然后生成包含正常数据点和离群点的样本数据。其中，正常数据点集中在以(2, 2)和(-2, -2)为中心的两个簇内，离群点则在整个空间内随机分布。

        创建一个ground_truth数组，用于标记每个数据点是否为离群点。其中，正常数据点标记为1，离群点标记为-1。

        使用LocalOutlierFactor类创建LOF模型，并设置参数，如邻居数量（n_neighbors）和污染度（contamination）。

        使用fit_predict方法拟合模型并预测样本点的标签。值得注意的是，在使用LOF进行离群检测时，没有“预测”这一说法，而是通过计算negative_outlier_factor_属性获得异常程度的分数。

        根据预测的标签和异常程度的分数，绘制散点图。其中，蓝色点表示数据点，红色空心圆表示被识别为离群点的数据点，圆的半径与其离群程度成正比。

import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor

print(__doc__)

np.random.seed(42)

# 制造训练数据
X_inliers = 0.3 * np.random.randn(100, 2)
X_inliers = np.r_[X_inliers + 2, X_inliers - 2]

# 制造一些离群值
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.r_[X_inliers, X_outliers]

n_outliers = len(X_outliers)
ground_truth = np.ones(len(X), dtype=int)
ground_truth[-n_outliers:] = -1

# 拟合模型以进行离群值检测（默认）
clf = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
# 使用fit_predict计算训练样本的预测标签（当使用LOF进行离群值检测时，估计器没有预测，decision_function和score_samples方法）。
y_pred = clf.fit_predict(X)
n_errors = (y_pred != ground_truth).sum()
X_scores = clf.negative_outlier_factor_

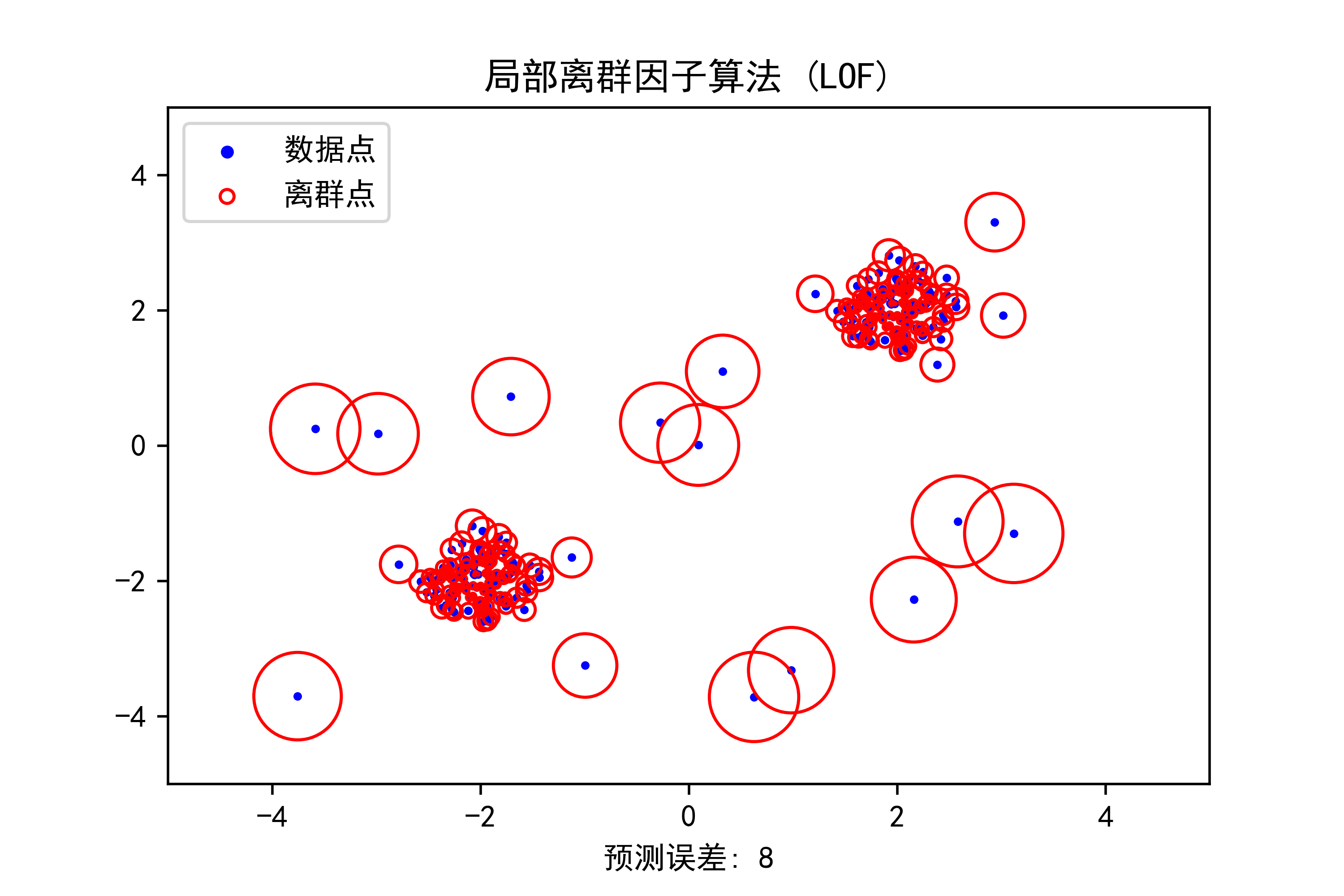
plt.title("局部离群因子算法 (LOF)")
plt.scatter(X[:, 0], X[:, 1], color='b', s=3., label='数据点')
# plot circles with radius proportional to the outlier scores
radius = (X_scores.max() - X_scores) / (X_scores.max() - X_scores.min())
plt.scatter(X[:, 0], X[:, 1], s=1000 * radius, edgecolors='r',
            facecolors='none', label='离群点')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.xlabel("预测误差: %d" % (n_errors))
legend = plt.legend(loc='upper left')
legend.legendHandles[0]._sizes = [10]
legend.legendHandles[1]._sizes = [20]
plt.show()

        示例运行结果如下图所示：

        数据点呈现出两个主要的聚类簇，分别位于(2, 2)和(-2, -2)。

        散点图中的红色空心圆表示被标记为离群点的数据点，它们分布在主要聚类簇的周围或孤立的区域。

        通过这个可视化结果，我们可以直观地观察到LOF算法对于检测离群点的效果，并识别出数据集中的异常情况。

 04-最近邻分类实战         

        最近邻居分类（K-Nearest Neighbors，简称KNN）是一种基于实例的、懒惰学习的监督学习算法。它的原理可以概括如下：

        距离度量：KNN基于距离度量来对样本进行分类。通常使用的距离度量方法是欧氏距离，但也可以根据实际情况选择其他距离度量方法。

        邻居选择：对于一个未知类别的样本，KNN算法会计算它与训练集中所有样本点的距离，并选择距离最近的K个样本点作为其最近邻居。

        投票表决：根据这K个最近邻居的类别标签，KNN算法采用投票表决的方式来确定未知样本的类别。通常，将未知样本归为K个最近邻居中出现最多次的类别。

        决策边界：KNN的决策边界是由各个类别的样本点组成的分界线，在特征空间中将不同类别的样本分开。

        参数K的选择：KNN中的一个关键参数是K值，它决定了邻居的数量。选择合适的K值对于KNN的性能至关重要，通常通过交叉验证等方法来确定最优的K值。

        KNN算法的优点包括简单易懂、无需训练过程等；缺点则包括对数据集规模敏感、计算复杂度高等。在实际应用中，KNN通常用于中小型数据集和低维特征空间的分类问题，以及作为其他算法的基准进行性能评估。

        下面给出示例代码分析分类过程的应用过程：这段代码首先导入了必要的库，并加载了鸢尾花数据集。然后，它循环遍历两种不同的权重参数（uniform和distance），每种参数对应一个图像。在每次循环中，它创建一个K近邻分类器实例并拟合数据，然后使用Meshgrid在特征空间中创建网格点，并对这些点进行分类预测，最后绘制决策边界和训练数据的散点图。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets

n_neighbors = 15

# 导入需要处理的数据
iris = datasets.load_iris()

# 我们仅采用前两个特征。我们可以通过使用二维数据集来避免使用复杂的切片
X = iris.data[:, :2]
y = iris.target

h = .02  # 设置网格中的步长

# 提取色谱
cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue'])
cmap_bold = ListedColormap(['darkorange', 'c', 'darkblue'])

for i, weights in enumerate(['uniform', 'distance']):
    # 我们创建最近邻分类器的实例并拟合数据。
    clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
    clf.fit(X, y)

    # 绘制决策边界。 为此，我们将为网格[x_min，x_max] x [y_min，y_max]中的每个点分配颜色。
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

    # 将结果放入颜色图
    Z = Z.reshape(xx.shape)
    plt.figure()
    plt.pcolormesh(xx, yy, Z, cmap=cmap_light)

    # 绘制训练数据
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
                edgecolor='k', s=20)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.title("3-Class classification (k = %i, weights = '%s')"
              % (n_neighbors, weights))
    plt.savefig("../plot_%d.png" % i, dpi=500)  # 保存当前图像
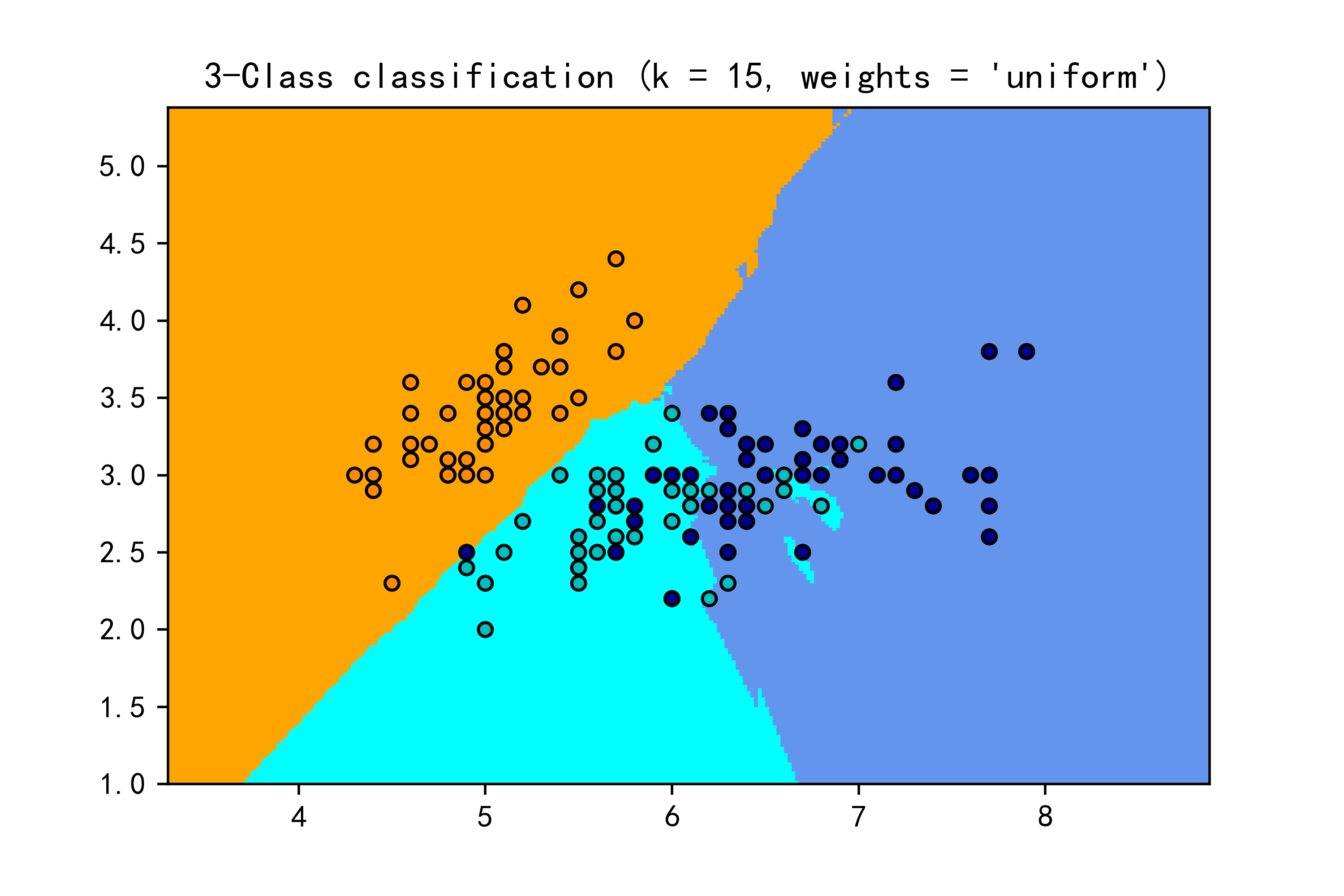
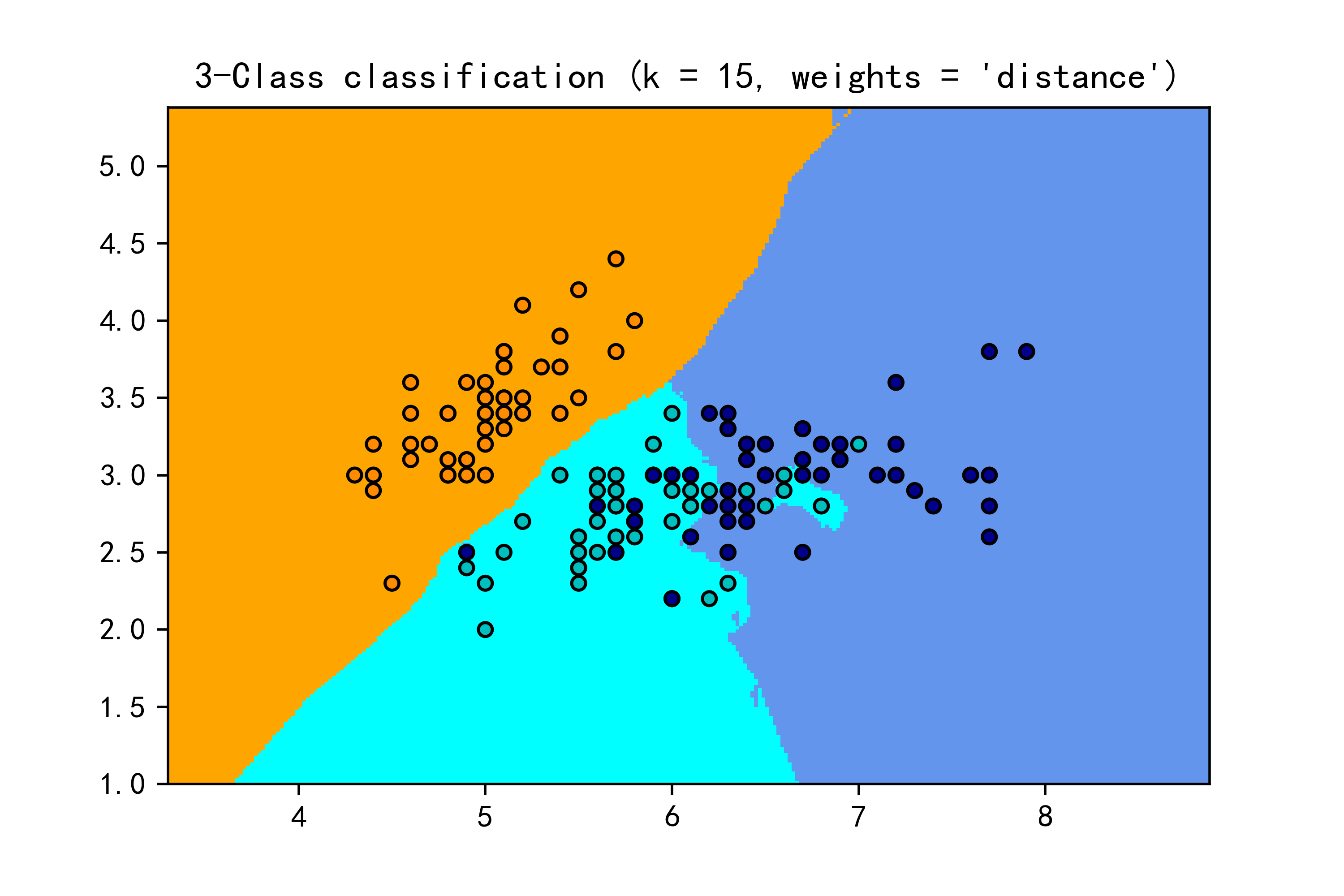
    plt.show()  # 展示当前图像

        示例运行结果如下图所示：第一张图使用的是uniform权重，它将所有最近邻的样本点视为同等重要，因此决策边界比较平滑，各个类别的样本点区分度不太明显。第二张图使用的是distance权重，它考虑了最近邻样本点的距离权重，因此决策边界更贴近各个类别的样本点，更能反映出样本分布的局部特征，使得分类边界更清晰。

05-最近邻质心分类实战         

        最近邻质心分类（Nearest Centroid Classification）是一种简单但有效的分类算法，它基于样本的类别质心来进行分类。其原理可以概括如下：

        质心计算：首先，对于每个类别，计算该类别所有样本的特征均值，得到该类别的质心（centroid）。质心是该类别样本在特征空间中的平均位置。

        距离度量：对于一个未知样本，计算它与每个类别质心之间的距离，通常使用欧氏距离或其他距离度量方法。

        分类决策：将未知样本分配给距离最近的类别质心所对应的类别。

        决策边界：分类决策边界是由各个类别质心组成的分界线，在特征空间中将不同类别的样本分开。

        最近邻质心分类的优点包括简单易懂、计算效率高等；缺点则包括对特征空间中样本分布的假设较强、对异常值敏感等。在实际应用中，最近邻质心分类通常用于处理线性可分的数据集，并且适用于低维特征空间的分类问题。

        下面给出示例代码分析分类过程的应用过程：

        这段代码首先导入了所需的库，并加载了鸢尾花数据集。然后，它定义了一个循环，其中shrinkage分别为None和0.2两种情况。在每次循环中，它创建了一个最近邻分类器的实例，并使用fit方法拟合数据。

        接下来，它定义了一个网格，根据数据的范围和指定的步长h，生成了一系列点。然后，对于每个点，使用分类器预测其所属类别，并在对应位置绘制出预测结果的决策边界。

        在循环内部，每次循环都会生成一张图像。图像中包含了决策边界和训练数据的散点图。最后，通过调用plt.savefig方法保存图像，文件名包含了当前循环的shrinkage值。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import datasets
from sklearn.neighbors import NearestCentroid

n_neighbors = 15

# 导入需要处理的数据
iris = datasets.load_iris()
# 我们仅采用前两个特征。我们可以通过使用二维数据集来避免使用复杂的切片
X = iris.data[:, :2]
y = iris.target

h = .02  # 设置网格中的步长

# 提取色谱
cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue'])
cmap_bold = ListedColormap(['darkorange', 'c', 'darkblue'])

for shrinkage in [None, .2]:
    # 我们创建最近邻分类器的实例并拟合数据。
    clf = NearestCentroid(shrink_threshold=shrinkage)
    clf.fit(X, y)
    y_pred = clf.predict(X)
    print(shrinkage, np.mean(y == y_pred))
    # 绘制决策边界。为此，我们将为网格[x_min，x_max] x [y_min，y_max]中的每个点分配颜色。
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

    # 将结果放入颜色图
    Z = Z.reshape(xx.shape)
    plt.figure()
    plt.pcolormesh(xx, yy, Z, cmap=cmap_light)

    # 绘制训练数据
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
                edgecolor='k', s=20)
    plt.title("3-Class classification (shrink_threshold=%r)"
              % shrinkage)
    plt.axis('tight')
    
    # 保存图像
    plt.savefig(f"classification_{shrinkage}.png")

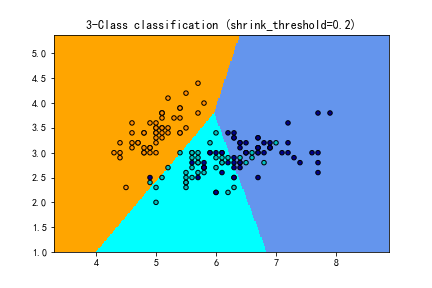
plt.show()

        示例运行结果如下图所示：对于生成的两张图像，第一张图像对应shrinkage为None时，第二张图像对应shrinkage为0.2时。在每张图像中，决策边界将不同程度地考虑了每个类别中心的重要性，这是由shrinkage参数控制的。因此，两张图像展示了在不同shrinkage下的分类效果。 

总结             

       k近邻回归（kNN Regression）：

        概述：k近邻回归是一种用于回归任务的非参数算法。它通过对其k个最近邻居的输出进行平均来预测查询点的输出。

        过程：聚合这些邻居的输出以预测查询点的输出，通常通过取它们的输出的平均值或加权平均值来实现。基于计算出的距离选择k个最近邻居。计算查询点与数据集中所有其他点之间的距离。

        参数：k：考虑的最近邻居的数量。距离度量：通常使用欧氏距离，但也可以使用其他度量标准，如曼哈顿距离。

        优点：简单直观。不对基础数据分布进行假设。

        缺点：对于大型数据集而言计算成本高昂。对k和距离度量的选择敏感。

        k近邻分类（kNN Classification）：

        概述：k近邻分类是一种用于分类任务的非参数算法。它根据其k个最近邻居中的多数类别分配查询点的类标签。

        过程：计算查询点与数据集中所有其他点之间的距离。基于计算出的距离选择k个最近邻居。根据邻居中的多数类别为查询点分配类标签。

        参数：k：考虑的最近邻居的数量。距离度量：与k近邻回归类似。

        优点：简单易用。对具有非线性决策边界的分类任务有效。

        缺点：需要谨慎选择k以避免过拟合或欠拟合。可能对噪声或无关特征敏感。

        局部离群因子算法（Local Outlier Factor，LOF）：

        概述：LOF是一种用于离群点检测的无监督算法。它衡量数据点与其邻居之间的局部密度的局部偏差。

        过程：对每个数据点，基于其与其k个最近邻居的距离计算局部密度。计算每个数据点的局部离群因子，该因子衡量对象与其邻居的偏差程度。具有显著高于邻居的LOF的数据点被视为离群点。

        参数：k：考虑的邻居数量。

        优点：在高维数据集中有效检测离群点。不假设特定的数据分布。

        缺点：计算密集，特别是对于大型数据集而言。对k和基础数据分布的选择敏感。