本文介绍光栅幅值细分原理与实现。
光栅是工业测量领域中常见的传感器,如下图。主要厂家有雷尼绍,海德汉,配套的光栅读数头有模拟信号的,也有直接细分输出数字脉冲的,本文的细分针对模拟信号,即有正弦信号,余弦信号,Index信号输出的光栅读数头。光栅细分方法有很多(如锁相倍频细分法,幅值细分法等),本文介绍常用的幅值细分法。

1.细分原理
由于常见的光栅栅距为20um,40um,对应一个正弦或余弦周期输出,分辨率太低,因此需要采用相应的细分方法,将分辨率调整到合适的值,如采用1000细分,可将栅距为20um的光栅尺,分辨率调高到20/1000um=0.02um。
幅值细分法是根据莫尔信号幅值和相位的对应关系,通过对幅值大小的分割判断来实现莫尔信号的相位细分。传统的幅值细分法利用电压比较器组将幅值信号与参考电压信号比较来输出细分脉冲,由于光栅传感器输出的莫尔信号波形近似正弦信号,如下图,在不同的相位处所对应的灵敏度不同,当信号幅值接近峰值时需要较大的相位变化才能引起微小的幅值变化,因此容易造成细分误差。
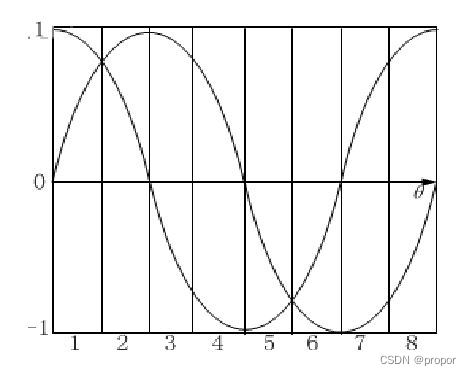
为了克服莫尔信号灵敏度不等造成细分误差的缺点,通常采用构造新函数的方法,以提高信号的线性度,这里采用正切函数构造的方法。
1)正切函数构造原理
设光栅传感器输出的2路莫尔信号为:
则可构造如下正切函数:
其中,
a)为光栅信号相位
b)A为光栅信号幅值,通常2个信号的幅值是相同的
构造的正切函数波形如下图。
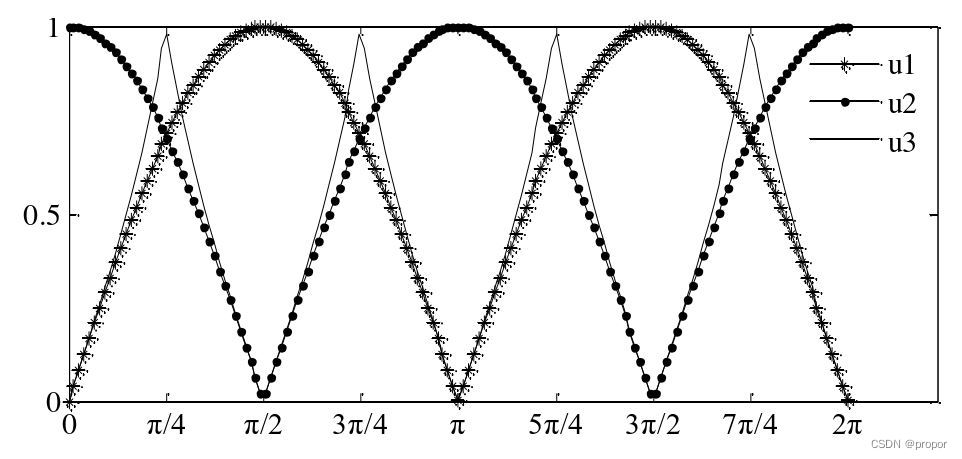
新函数近似三角波,是一个周期函数,包含一半正切函数波形,一半余切函数波形。采用这种方法的线性度高,且不需要确定莫尔信号的峰值大小,不易受信号衰减的影响,因此,幅值细分法得到了广泛的应用。
2)区间划分
由于不同的区间采用的函数是不一样的,为了便于信号处理,将整个周期划分为8个区间,当前信号所处的区间可由和
极性,
和
大小关系来进行确定。区间划分如下表。
| 区间 | |||
| 1 | + | + | |
| 2 | + | + | |
| 3 | + | - | |
| 4 | + | - | |
| 5 | - | - | |
| 6 | - | - | |
| 7 | - | + | |
| 8 | - | + |
3)区间细分数确定
设N为一个周期内总细分数。为了方便计算,我们将8个区间的计算统一映射到第1个区间,得到在不同区间的细分数值,如下表。
| 区间 | 细分数 |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
其中,
a)和
为各自区间的电压值
b)区间可由“2)区间划分”确定
2.细分实现
清楚原理,细分实现就比较简单了,细分实现框图如下图。
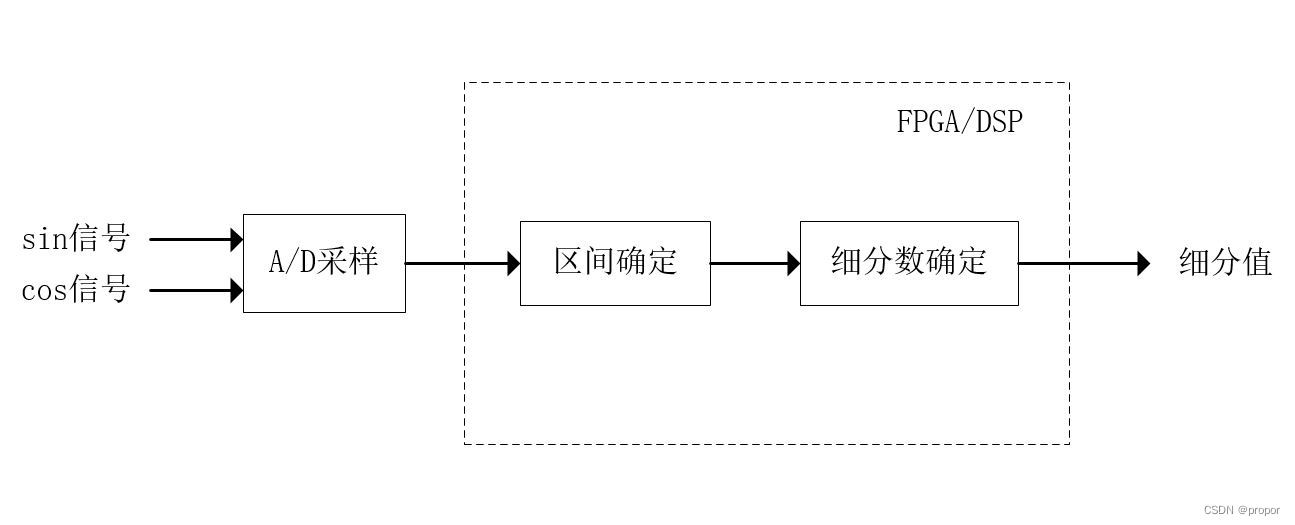
总的流程如下:
1)FPGA/DSP通过同步高速A/D采样,获取sin信号和cos信号幅值
2)FPGA/DSP通过区间划分表获取当前区间
3)FPGA/DSP通过当前区间,计算当前细分数
4)当信号经过一个周期后,总细分数加1
5)输出当前细分值
3.细分误差来源
造成细分误差的来源有很多,主要有以下几种:
1)直流误差。光栅输出正弦信号和余弦信号直流偏置不一样,造成A/D采样幅值不一样,从而造成计算相位时的误差。
2)幅值误差。光栅输出正弦信号和余弦信号幅值不一样,造成A/D采样幅值不一样,从而造成计算相位时的误差。
3)正交误差。光栅输出正弦信号和余弦信号有相位差,在计算相位时出现误差,可以通过示波器的李沙育图的圆度来判断。
可以通过误差补偿的方法减小误差,误差补偿顺序应遵循先进行直流补偿,再进行幅值补偿,最后进行正交补偿。
本文介绍了光栅幅值细分原理与实现。