目录
详细布置:
1. 层序遍历
2. 226. 翻转二叉树
3. 101. 对称二叉树
详细布置:
1. 层序遍历
昨天练习了几种二叉树的深度优先遍历,包括:
- 前中后序的递归法
- 前中后序的迭代法
- 前中后序迭代的统一写法
今天,将会练习下一种遍历方式:层序遍历,是图论中的广度优先遍历。
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历,动画如下:
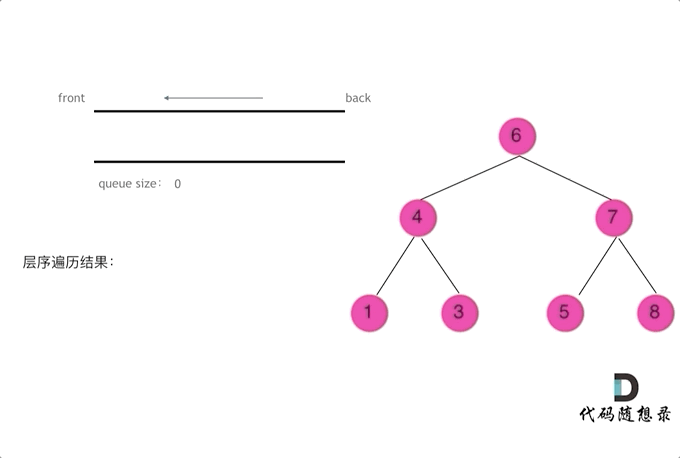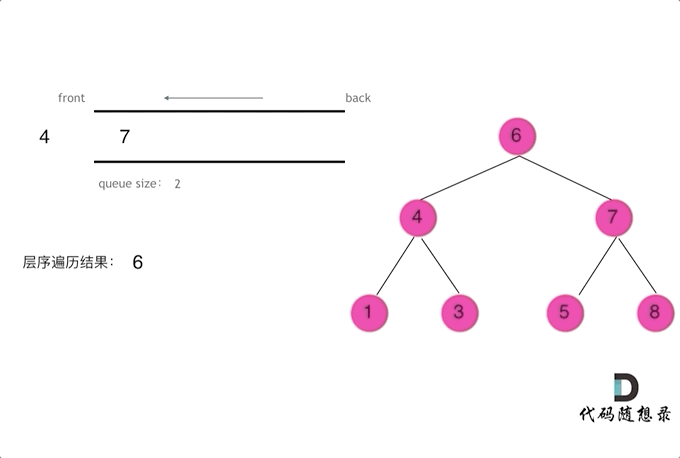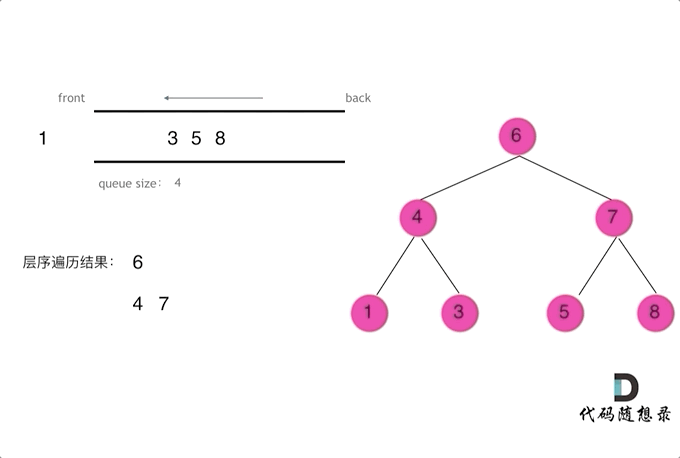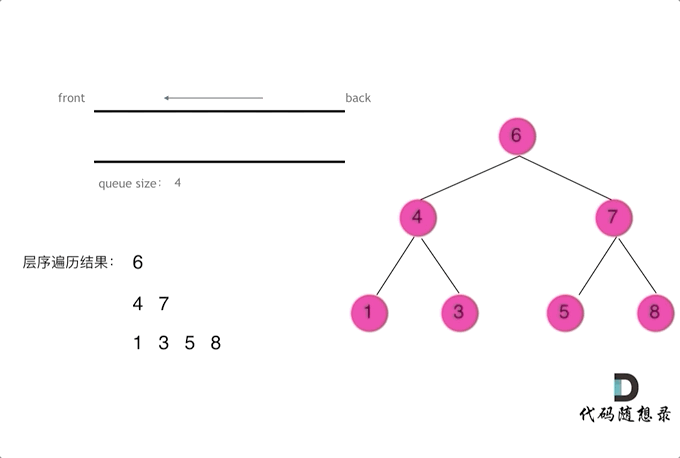
来源:代码随想录
Python代码实现如下:
# 利用长度法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root])
result = []
while queue:
level = []
for _ in range(len(queue)):
cur = queue.popleft()
level.append(cur.val)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
result.append(level)
return result# 递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
levels = []
self.helper(root, 0, levels)
return levels
def helper(self, node, level, levels):
if not node:
return
if len(levels) == level:
levels.append([])
levels[level].append(node.val)
self.helper(node.left, level + 1, levels)
self.helper(node.right, level + 1, levels)有了这个模版,可以一下解决十道力扣题:
- 102.二叉树的层序遍历
- 107.二叉树的层次遍历II
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的层序遍历
- 515.在每个树行中找最大值
- 116.填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
- 104.二叉树的最大深度
- 111.二叉树的最小深度
2. 226. 翻转二叉树
给你一棵二叉树的根节点
root,翻转这棵二叉树,并返回其根节点。
建议:这道题目 一些做过的同学 理解的也不够深入,建议大家先看我的视频讲解,无论做过没做过,都会有很大收获。
# 迭代法:广度优先遍历(层序遍历):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
queue = collections.deque([root])
while queue:
for i in range(len(queue)):
node = queue.popleft()
node.left, node.right = node.right, node.left
if node.left: queue.append(node.left)
if node.right: queue.append(node.right)
return root
3. 101. 对称二叉树
给你一个二叉树的根节点
root, 检查它是否轴对称。
建议:先看视频讲解,会更容易一些。
# 层次遍历
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
queue = collections.deque([root.left, root.right])
while queue:
level_size = len(queue)
if level_size % 2 != 0:
return False
level_vals = []
for i in range(level_size):
node = queue.popleft()
if node:
level_vals.append(node.val)
queue.append(node.left)
queue.append(node.right)
else:
level_vals.append(None)
if level_vals != level_vals[::-1]:
return False
return True