算法与数据结构：二叉排序树与AVL树

news2024/11/17 9:39:19

    ACM大牛带你玩转算法与数据结构-课程资料

 本笔记属于船说系列课程之一，课程链接：

哔哩哔哩_bilibiliicon-default.png?t=N7T8https://www.bilibili.com/cheese/play/ep66799?csource=private_space_class_null&spm_id_from=333.999.0.0

你也可以选择购买『船说系列课程-年度会员』产品『船票』，畅享一年内无限制学习已上线的所有船说系列课程：船票购买入口icon-default.png?t=N7T8https://www.bilibili.com/cheese/pages/packageCourseDetail?productId=598

做题网站OJ：HZOJ - Online Judge

Leetcode :力扣 (LeetCode) 全球极客挚爱的技术成长平台

二叉排序树  ​

构建二叉排序树：

        数据结构 = 结构定义 + 结构操作

结构定义：

        这个数据结构是靠二叉树来得到的，那么我们就先定义树形结构，而树形结构是由节点构成的，那么最终我们定义一个节点的结构体，以及对节点的初始化操作和清空操作：

//定义节点结构
typedef struct Node {
    int key;
    struct Node *lchild, *rchild;
} Node;

//初始化
Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->lchild = p->rchild = NULL;
    return p;
}

//清空
void clear(Node *root) {
    if (root == NULL) return ;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}
结构操作：

        在对结构定义完成后，那么就是开始定义结构操作了，那就是对二叉排序的增加节点和删除节点：

        增加节点

        由于增加节点的操作比较简单，就不做图来解释了：

//和之前学习树时的插入节点是差不多的
//只是多了对二叉排序树性质的判断
Node *insert(Node *root, int key) {
    if (root == NULL) return getNewNode(key);
    //当插入值等于当前节点值时,返回当前节点，说明不用插入该节点
    if (key == root->key) return root;
    //当插入值小于当前节点值时，往左子树递归进行插入
    if (key < root->key) root->lchild = insert(root->lchild, key);
    //当插入值大于当前节点值时，往右子树递归进行插入
    else root->rchild = insert(root->rchild, key);
    return root;
}
        删除节点

        删除节点时，需要判断当前删除的节点的度：

  • 删除度为0的节点：直接删除
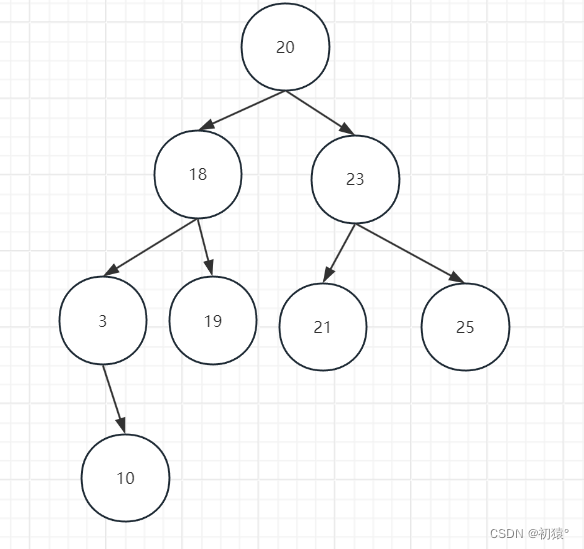
  • 删除度为1的节点：

        如图一个排序二叉树，当前如果删除的节点为3，而它的度为1，可以直接删除，然后接在18的左子树上，也不会影响二叉排序树的性质。

        


         

  • 删除度为2的节点：

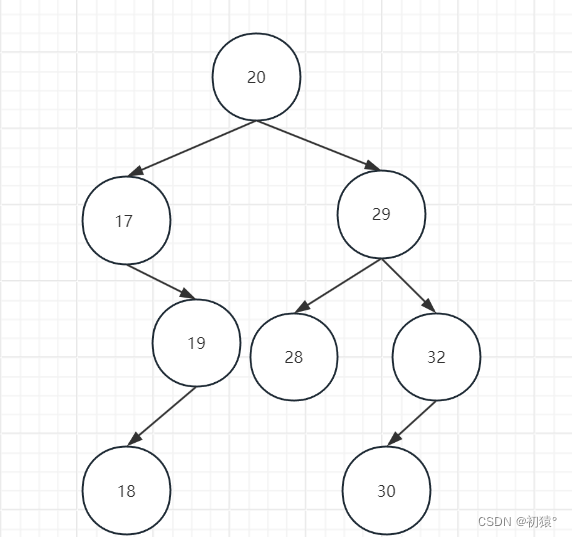
        如图下面的二叉树：

        

        如何去删除20号节点，我们需要找20对应中序遍历的前驱节点或者后继节点：

        通过发现二叉树的中序遍历就是一个升序序列，而图中的中序遍历为：

        17 18 19 20 28 29 30 32

        看20这个节点，19是它的前驱，28是他的后继，可以发现前驱就是当前节点左子树的最大值，后继就是当前节点右子树的最小值。

        那么如果通过二叉排序怎么去找到当前节点的前驱和后继呢：

        前驱：先进入当前节点的左子树然后一直往右子树一直找，直到没有右子树，那么当前节点就是它的前驱节点。

        后继：同理先进入当前节点右子树，一直往左子树找，然后没有左子树，那么当前节点就是它的后继节点。

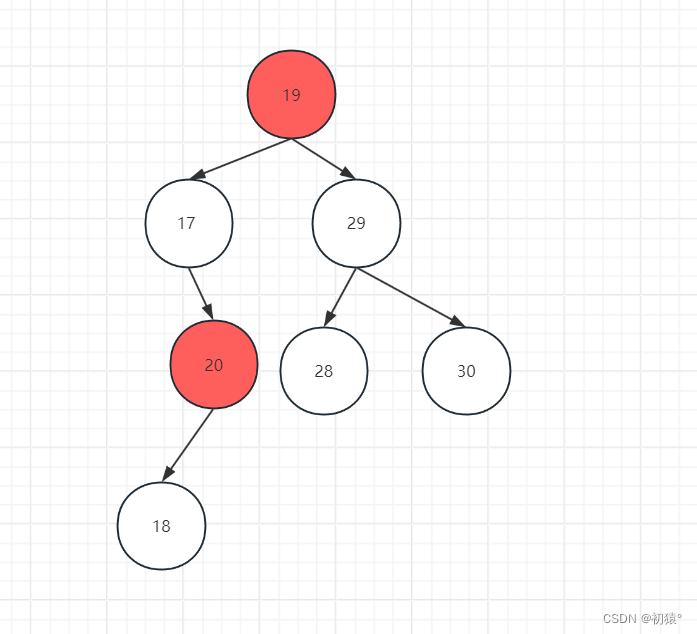
        得到它的前驱和后继有什么用呢，可以把需要删除的节点和他的前驱或者后继进行交换位置，然后就可以变成删除度为1的节点或者删除度为0的节点的问题了。因为它的前驱或者后继它的度一定是小于等于1的，因为前驱和后继一个是没有右子树一个是没有左子树的。

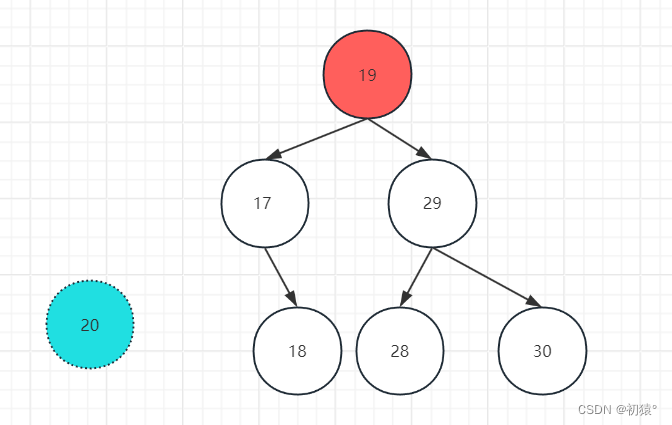
        如图，20和它的前驱节点19发生了交换，并且19在那个节点上满足二叉排序树的性质。

        然后进行对20节点的删除，也就是删除度为1的节点的方法。

 有了思路后，通过思路去实现代码：

//找到删除节点的前驱节点
Node *predecessor(Node *root) {
    Node *temp = root->lchild;
    while (temp->rchild) temp = temp->rchild;
    return temp;
}

Node *erase(Node *root, int key) {
    if (root == NULL) return root;
    //先通过二叉树的性质,递归找到需要删除的节点
    if (key < root->key) root->lchild = erase(root->lchild, key);
    else if (key > root->key) root->rchild = erase(root->rchild, key);
    //找到需要删除的节点
    else {
        //度为0的节点删除
        if (root->lchild == NULL && root->rchild == NULL) {
            free(root);
            return NULL;
        } 
        //度为1的节点删除
        else if (root->lchild == NULL || root->rchild == NULL) {
            //先通过一个变量记录删除节点的左子树或者右子树
            Node *temp = root->lchild ? root->lchild : root->rchild;
            //删除节点
            free(root);
            //然后将删除节点的左子树或右子树接上
            return temp;
        } 
        //度为2的节点删除
        else {
            //这里是用的是找前驱节点
            Node *temp = predecessor(root);
            //直接把删除节点的值用前驱节点的值覆盖掉
            root->key = temp->key;
            //然后通过递归调用去删除前驱节点
            root->lchild = erase(root->lchild, temp->key);
        }
    }
    return root;
}
完整代码：
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define KEY(n) (n ? n->key : -1)

typedef struct Node {
    int key;
    struct Node *lchild, *rchild;
} Node;

Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->lchild = p->rchild = NULL;
    return p;
}

//和之前学习树时的插入节点是差不多的
//只是多了对二叉排序树性质的判断
Node *insert(Node *root, int key) {
    if (root == NULL) return getNewNode(key);
    //当插入值等于当前节点值时,返回当前节点，说明不用插入该节点
    if (key == root->key) return root;
    //当插入值小于当前节点值时，往左子树递归进行插入
    if (key < root->key) root->lchild = insert(root->lchild, key);
    //当插入值大于当前节点值时，往右子树递归进行插入
    else root->rchild = insert(root->rchild, key);
    return root;
}

//找到删除节点的前驱节点
Node *predecessor(Node *root) {
    Node *temp = root->lchild;
    while (temp->rchild) temp = temp->rchild;
    return temp;
}

Node *erase(Node *root, int key) {
    if (root == NULL) return root;
    //先通过二叉树的性质,递归找到需要删除的节点
    if (key < root->key) root->lchild = erase(root->lchild, key);
    else if (key > root->key) root->rchild = erase(root->rchild, key);
    //找到需要删除的节点
    else {
        //度为0的节点删除
        if (root->lchild == NULL && root->rchild == NULL) {
            free(root);
            return NULL;
        } 
        //度为1的节点删除
        else if (root->lchild == NULL || root->rchild == NULL) {
            //先通过一个变量记录删除节点的左子树或者右子树
            Node *temp = root->lchild ? root->lchild : root->rchild;
            //删除节点
            free(root);
            //然后将删除节点的左子树或右子树接上
            return temp;
        } 
        //度为2的节点删除
        else {
            //这里是用的是找前驱节点
            Node *temp = predecessor(root);
            //直接把删除节点的值用前驱节点的值覆盖掉
            root->key = temp->key;
            //然后通过递归调用去删除前驱节点
            root->lchild = erase(root->lchild, temp->key);
        }
    }
    return root;
}

void clear(Node *root) {
    if (root == NULL) return ;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

void output(Node *root) {
    if (root == NULL) return ;
    printf("(%d ; %d, %d)\n", 
        KEY(root), 
        KEY(root->lchild),
        KEY(root->rchild)
    );
    output(root->lchild);
    output(root->rchild);
    return ;
}

void in_order(Node *root) {
    if (root == NULL) return ;
    in_order(root->lchild);
    printf("%d ", root->key);
    in_order(root->rchild);
    return ;
}

int main() {
    srand(time(0));
    #define MAX_OP 10
    Node *root = NULL;
    for (int i = 0; i < MAX_OP; i++) {
        int key = rand() % 100;
        printf("insert key %d to BST\n", key);
        root = insert(root, key);
    }
    output(root);
    printf("in order : ");
    in_order(root);
    printf("\n");
    

    int x;
    while (~scanf("%d", &x)) {
        printf("erase %d from BST\n", x);
        root = erase(root, x);
        in_order(root); printf("\n");
    }
    return 0;

}

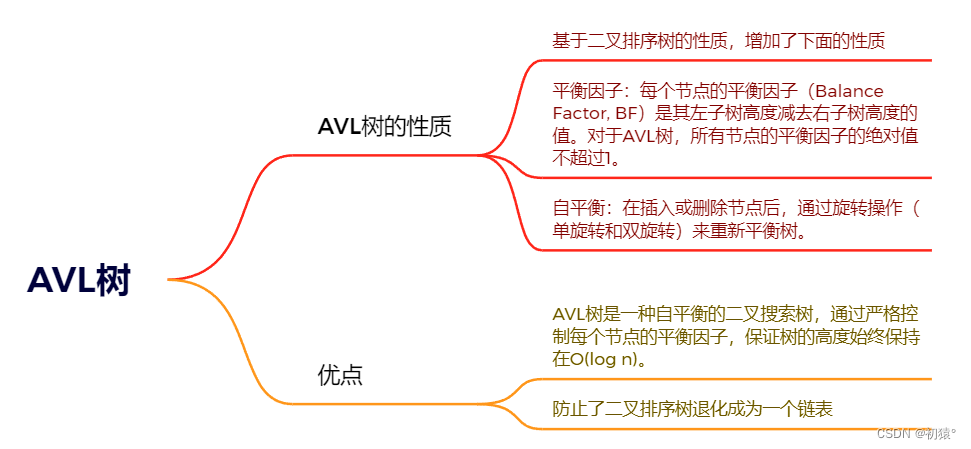
AVL树 

        为什么会有AVL树，先来看一个二叉排序树：

        

        通过发现，这颗二叉排序树退化成了链表，然后它的结构操作时间复杂度都降到了O(n)的级别。而二叉排序树的优点又是这些操作的时间复杂度都是O(logn)的，然后为了保证时间复杂度就有人发明了AVL树：

        AVL是通过选择操作来进行将左右子树的高度差控制在小于等于1的范围内的！！！

通过旋转平衡二叉树

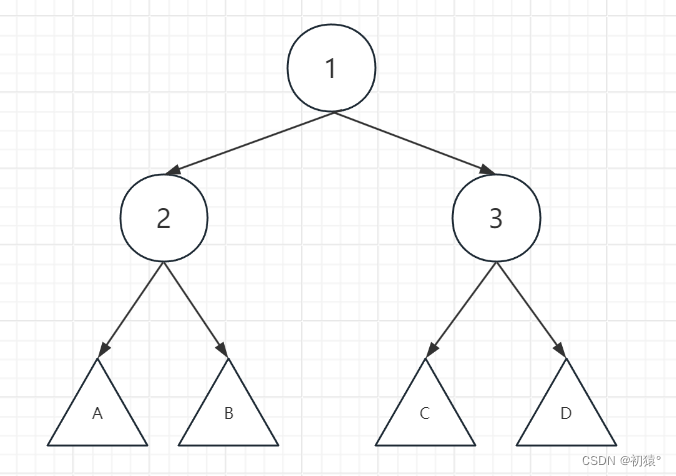
左旋（右旋同理)

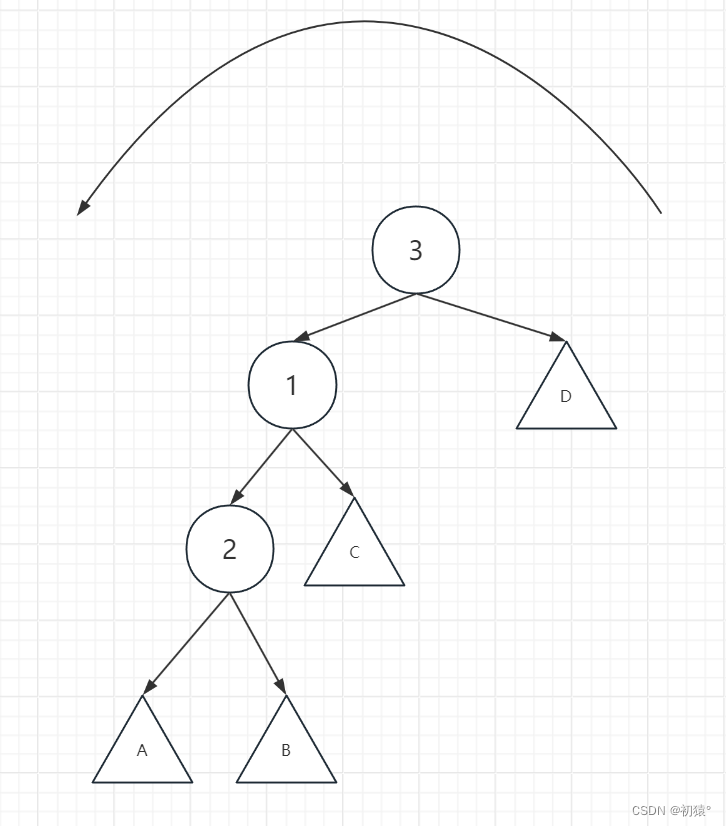
         如图这是一颗二叉排序树，1，2，3为节点，AB为2的左右子树，CD为3的左右子树。

        现在我通过1节点左旋：

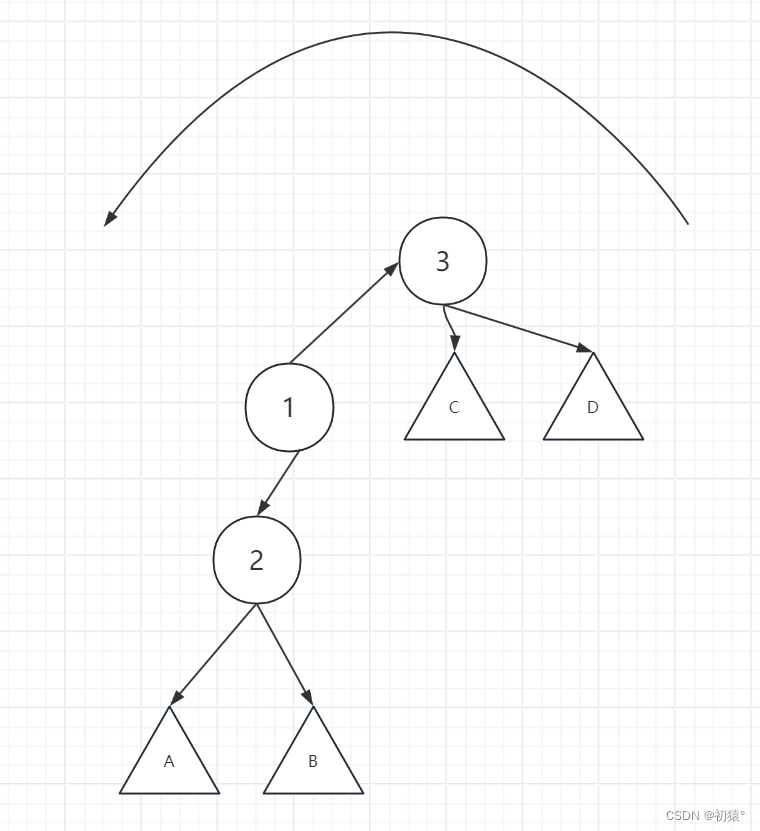
        如何去理解这个过程，现在我拎着节点3，把节点3拎到节点1的位置去，1就该往下沉一层到节点2的位置，2节点下面的子树也应该往下沉一层
 

          那么现在应该是这样一个样子，将3的左子树指向节点1，因为节点1小于节点3，所以节点1作为节点3的左孩子是没有破坏二叉排序树的性质的。

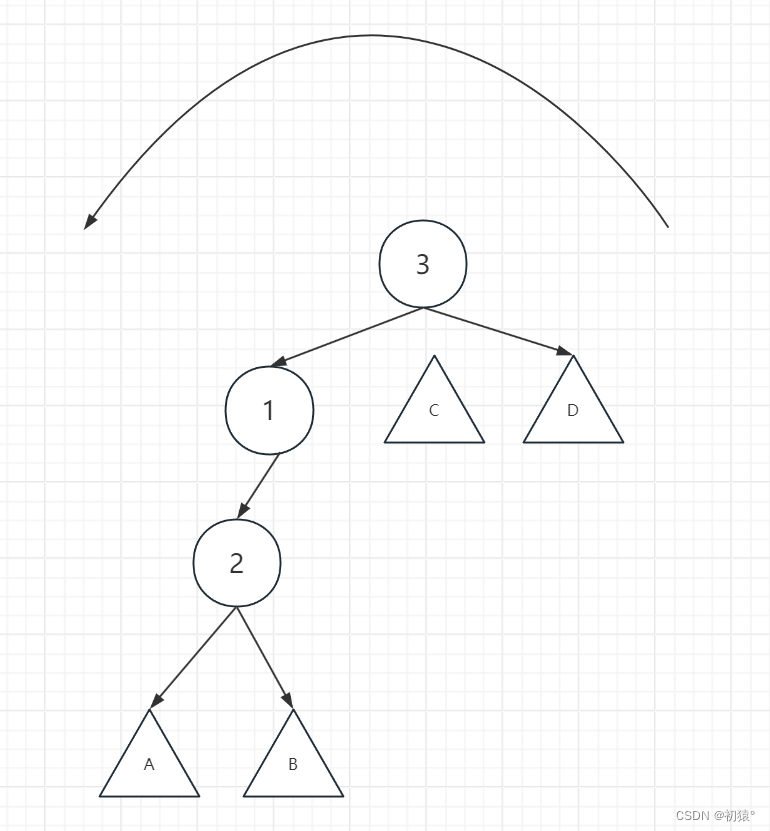
        然后C子树现在没有节点指向了，节点1又没有右子树，那么节点1的右子树就指向C子树。

        然后证明C子树接在节点1的位置上不破坏二叉排序树的性质，通过最开始这张图来进行分析，C子树在1的右子树，那么C子树中的节点一定是大于1节点的值，所以c子树是可以直接接在1节点上，并且不会破坏二叉排序树的性质，最后完成了左旋操作。

        右旋操作和左旋操作差不了太多，也就是换了一个方向，同理可以推断出来，所以不详细的模拟了。

AVL树的平衡操作

        有了左旋和右旋操作的了解，下面通过左旋和右旋来进行对AVL的平衡调整：

        AVL树的失衡类型：
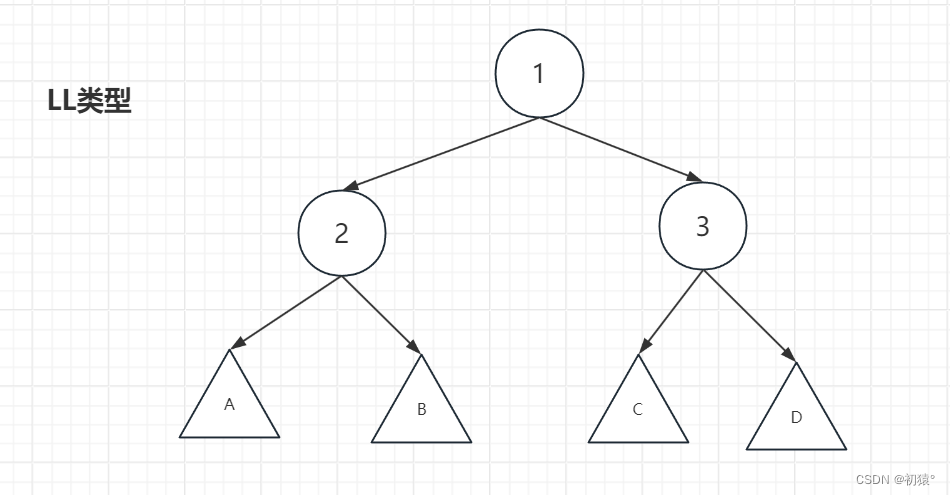
                LL类型和RR类型：
        

        对于图中就是失衡的子树。

        注意是子树，不要把图中的树看为一整颗树，需要看一颗子树，它可能是某一颗大树的子树。

        还需要注意的是节点1是从上到下往上看第一个失衡的节点，对于结点2来看它和它的子树是平衡的，节点3来看他和它的子树是平衡的，ABCD子树都是平衡的，但是从节点1来看他是失衡的。

        失衡的子树，也就是子树高度最高的子树，然后如果失衡子树在失衡节点的左孩子的左子树那么就为LL，右孩子的右子树为RR，左孩子的右子树为LR，右孩子的左子树为RL。

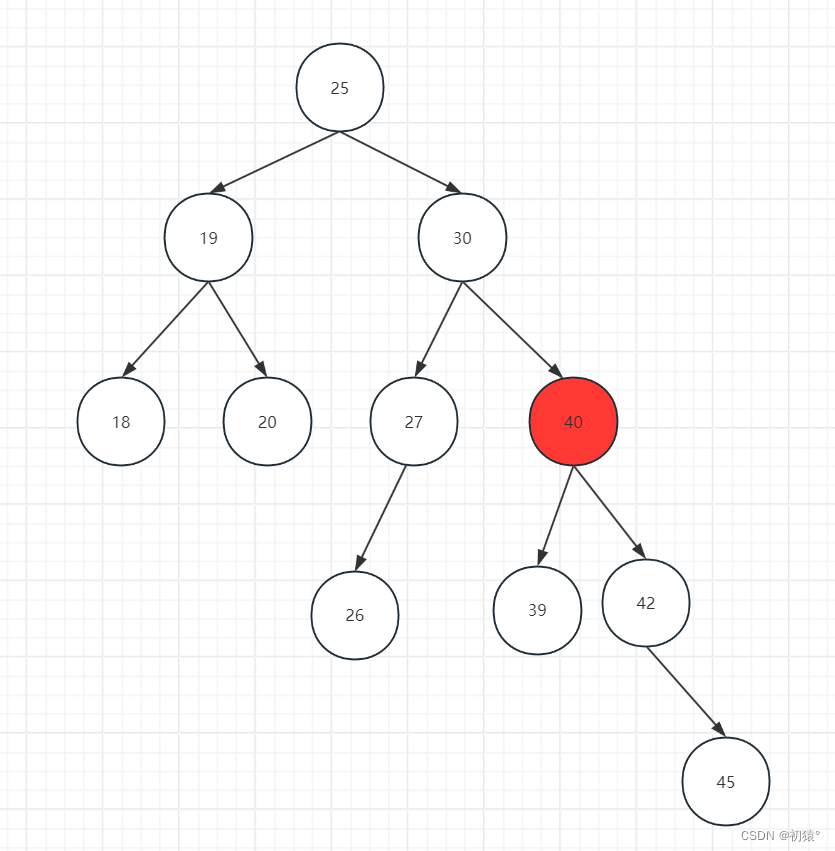
        比如这颗子树，它就是RR类型，从节点25来看它是失衡的，但是从下面任何一个节点来看它都是平衡的，那么40这个节点加上它的子树就为造成失衡的子树。

        图中红色标记的子树是高度最高的子树，也就是造成从节点1来看让这颗子树失衡的子树。也就是说从节点1来看：

        h(3) - h(2) > 1了，造成了失衡。

        那么如何去调整，就需要用到左旋和右旋。

        对于LL的处理：

        直接通过对节点1的一个右旋就可以平衡二叉树：

       h(x)为旋转前高度,H(x)为旋转后的高度

       旋转前:

        h(2) = h(3) + 2,因为失衡可以得到

        h(2) = h(a) + 1,因为a为高一点的子树，所以可以推断得到

        h(b) = h(a) - 1,因为a子树比b子树高一层

        h(3) = max(h(c),h(d)) + 1

        通过上面的式子可以得到

        h(a) = max(h(c),h(d)) + 2

        旋转后:

        通过节点2来看，子树A和节点1的高度差为，A的高度去减去节点1的高度，而节点1的高度要么是B的高度+1或者3的高度+1，通过上面的式子可以得到B的高度+1等于A，所以如果B+1高度为节点1的高度，那么不会失衡，如果节点3的高度+1作为节点1的高度，那么

        h(a) - (h(3) + 1) = max(h(c),h(d)) + 2 - (max(h(c),h(d)) + 1 + 1) = 0

        也是处于平衡状态，所以从节点2来看二叉树是平衡的，

        又从节点1来看，b的高度为h(b) = h(a) - 1 = max(h(c),h(d)) + 1,和h(3)的高度一样，所以从节点1来看二叉树也是平衡的，3节点更不用判断了他从开始没变过那么也是平衡的

        最终LL类型通过右旋可以让失衡状态转为平衡，同理RR类型一样左旋就可以达到平衡。

LR类型和RL类型：

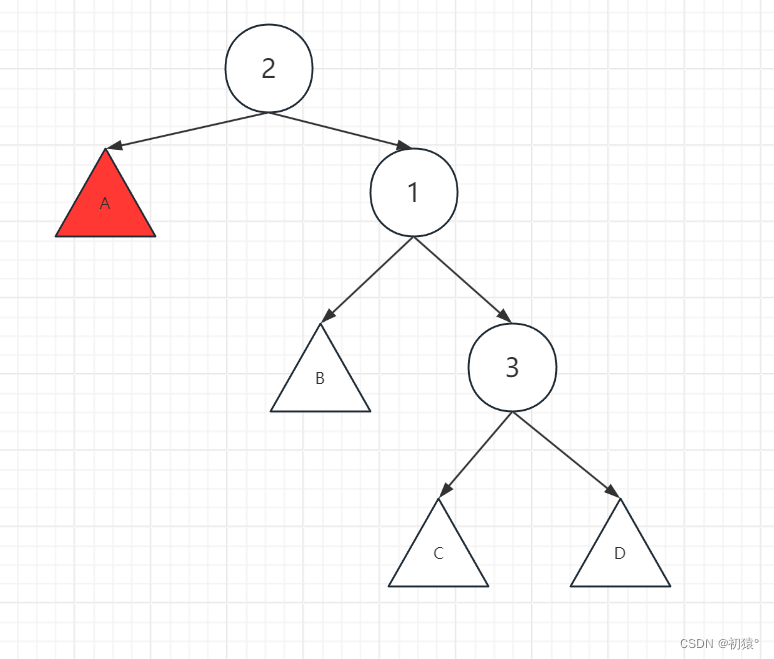
        LR和RL类型如何去处理，例如LR类型：

        

        由于失衡那么 h(2) = h(d) + 2

        h(1) = max(h(b), h(c)) + 1

        h(a) = h(1) - 1

        h(2) = h(1) + 1

        所以h(a) = max(h(b), h(c))

               h(d) = h(2) - 2 = h(1) - 1 = max(h(c), h(b)) = h(a)

        先通过节点2的一个左旋，这样就能得到一个LL类型

        如何得到的

        h(2) = h(a) + 1

        h(1) = h(2) + 1 = h(a) + 2

        又h(a) = h(d)

        所以较高的子树跑到左边去，也就是LR中的R中较高的子树变为了L了，通过节点2的左旋就可以得到LL类型，

        然后再通过节点3的一个右旋，就可以让这课树平衡了：

        

        现在h(2) = h(a) + 1

               h(3) = max(h(c), h(d)) + 1 = max(h(c), h(a)) + 1 = h(a) + 1

               h(2) - h(3) <= 1所以平衡

代码实现

        了解为什么要将二叉排序进行平衡操作和理解了通过左旋和右旋的方式将二叉排序树进行平衡后，下面进行代码实现：

        结构定义

        这里用到了一段代码：

__attribute__((constructor))

        它的作用就是，在main函数之前执行他设置的函数，对应代码段中那就是先执行int_NIL 初始化__NIL节点的操作。

        关于它的说明：


//定义节点
typedef struct Node {
    int key, h;
    struct Node *lchild, *rchild;
} Node;

//定义一个全局变量__NIL，用来表示空节点
Node __NIL;
#define NIL (&__NIL)
//利用__attribute__((constructor)) 用来设置init_NIL函数先于main主函数执行
//用来初始化NIL节点
//NIL节点用来表示空节点，这是一个编码小技巧
__attribute__((constructor))
void init_NIL() {
    NIL->key = -1;
    NIL->h = 0;
    NIL->lchild = NIL->rchild = NIL;
    return ;
}

//获取新节点的初始化操作
Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->h = 1;
    p->lchild = p->rchild = NIL;
    return p;
}

//清除节点操作,采用后续遍历的方式进行清除
void clear(Node *root) {
    if (root == NIL) return ;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}
        结构操作
        平衡操作：
#define K(n) (n->key)
#define H(n) (n->h)
#define L(n) (n->lchild)
#define R(n) (n->rchild)

//更新高度
void update_height(Node *root) {
    //当前节点的高度等于左右子树最高的高度+1
    H(root) = (H(L(root)) > H(R(root)) ? H(L(root)) : H(R(root))) + 1;
    return ;
}

//左旋操作
Node *left_rotate(Node *root) {
    //左旋操作后
    //当前节点的右孩子应该在当前节点的位置
    //让后当前节点变为了，他右孩子的左子树
    //然后当前节点的右孩子的左子树指向了当前节点
    //所以当前节点的右子树应该去指向它之前的右孩子的左子树
    printf("left rotate : %d\n", root->key);
    //创建一个节点用来记录当前节点的右孩子
    Node *new_node = root->rchild;
    //那么当前节点的右子树就可以指向它之前的右孩子的左子树
    root->rchild = new_node->lchild;
    //右孩子的左子树指向了当前节点，那么右孩子就通过左旋操作
    //到了当前节点的位置上了
    //也就完成了左旋操作
    new_node->lchild = root;
    //然后更新当前节点的高度
    update_height(root);
    //更新右孩子的高度
    update_height(new_node);
    //其他节点的高度是没有改变的
    //因为右孩子替代了当前节点的位置
    //那么就返回右孩子
    return new_node;
}

//右旋操作
Node *right_rotate(Node *root) {
    //右旋操作同理反过来思考就可以了
    printf("right rotate : %d\n", root->key);
    Node *new_node = root->lchild;
    root->lchild = new_node->rchild;
    new_node->rchild = root;
    update_height(root);
    update_height(new_node);
    return new_node;
}

const char *type_str[5] = {
    "",
    "maintain type : LL",
    "maintain type : LR",
    "maintain type : RR",
    "maintain type : RL"
};

//平衡操作，也就是判断是LL,RR或者LR和RL类型
//然后再进行左右旋后平衡二叉树
Node *maintain(Node *root) {
    //判断当前子树是否左右子树平衡
    if (abs(H(L(root)) - H(R(root))) <= 1) return root;
    //这里的type只是起了最终演示的效果，用来进行debug和演示的
    int type = 0;
    //判断前面的字母,例如LR中的L
    if (H(L(root)) > H(R(root))) {
        //进入到这里说明是L？类型
        //下面if判断就是是否是LR类型，如果是先进行左旋
        if (H(R(L(root))) > H(L(L(root)))) {
            //说明是LR类型，那么先对当前节点的左子树进行左旋变为LL类型
            //下面会一起对LL类型进行处理
            root->lchild = left_rotate(root->lchild);
            type += 1;
        }
        //因为通过上面的if判断后，如果是LR类型，已经通过左旋变为LL类型
        //如果是LL类型那么上面的if里面的代码段也不会执行
        //所以这里直接右旋处理LL类型，将当前节点进行平衡
        root = right_rotate(root);
        type += 1;
    
    } 
    //这里就是前面字母是R类型了
    else {
        type = 2;
        //if判断是否是RL类型
        if (H(L(R(root))) > H(R(R(root)))) {
            //说明是RL类型，那么先将当前节点的右子树进行右旋
            root->rchild = right_rotate(root->rchild);
            type += 1;
        }
        //对于RR类型处理
        root = left_rotate(root);
        type += 1;
    }
    printf("%s\n", type_str[type]);
    //完成当前节点的平衡操作，返回
    return root;
}
        删除、插入、查找操作：

        

Node *insert(Node *root, int key) {
    //正常的二叉排序节点插入操作
    if (root == NIL) return getNewNode(key);
    if (root->key == key) return root;
    if (key < root->key) root->lchild = insert(root->lchild, key);
    else root->rchild = insert(root->rchild, key);
    //这是一个回溯的过程，所以是从下往上节点进行的下面的操作
    //更新每个节点的高度
    update_height(root);
    //返回平衡后的节点
    return maintain(root);
}

Node *predecessor(Node *root) {
    Node *temp = root->lchild;
    while (temp->rchild != NIL) temp = temp->rchild;
    return temp;
}

Node *erase(Node *root, int key) {
    //删除节点的操作和平衡二叉树一样
    if (root == NIL) return root;
    if (key < root->key) root->lchild = erase(root->lchild, key);
    else if (key > root->key) root->rchild = erase(root->rchild, key);
    else {
        if (root->lchild == NIL || root->rchild == NIL) {
            Node *temp = root->lchild != NIL ? root->lchild : root->rchild;
            free(root);
            return temp;
        } else {
            Node *temp = predecessor(root);
            root->key = temp->key;
            root->lchild = erase(root->lchild, temp->key);
        }
    }
    //然后主要的就是更新高度和平衡操作
    update_height(root);
    return maintain(root);
}

Node *find(Node *root, int key) {
    if (root == NIL) return NIL;
    if (root->key == key) return root;
    if (key < root->key) return find(root->lchild, key);
    return find(root->rchild, key);
}
        最终代码：

        

#include<stdio.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

//定义节点
typedef struct Node {
    int key, h;
    struct Node *lchild, *rchild;
} Node;

//定义一个全局变量__NIL，用来表示空节点
Node __NIL;
#define NIL (&__NIL)
#define K(n) (n->key)
#define H(n) (n->h)
#define L(n) (n->lchild)
#define R(n) (n->rchild)
//利用__attribute__((constructor)) 用来设置init_NIL函数先于main主函数执行
//用来初始化NIL节点
//NIL节点用来表示空节点，这是一个编码小技巧
__attribute__((constructor))
void init_NIL() {
    NIL->key = -1;
    NIL->h = 0;
    NIL->lchild = NIL->rchild = NIL;
    return ;
}

//获取新节点的初始化操作
Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->h = 1;
    p->lchild = p->rchild = NIL;
    return p;
}

//更新高度
void update_height(Node *root) {
    //当前节点的高度等于左右子树最高的高度+1
    H(root) = (H(L(root)) > H(R(root)) ? H(L(root)) : H(R(root))) + 1;
    return ;
}

//左旋操作
Node *left_rotate(Node *root) {
    //左旋操作后
    //当前节点的右孩子应该在当前节点的位置
    //让后当前节点变为了，他右孩子的左子树
    //然后当前节点的右孩子的左子树指向了当前节点
    //所以当前节点的右子树应该去指向它之前的右孩子的左子树
    printf("left rotate : %d\n", root->key);
    //创建一个节点用来记录当前节点的右孩子
    Node *new_node = root->rchild;
    //那么当前节点的右子树就可以指向它之前的右孩子的左子树
    root->rchild = new_node->lchild;
    //右孩子的左子树指向了当前节点，那么右孩子就通过左旋操作
    //到了当前节点的位置上了
    //也就完成了左旋操作
    new_node->lchild = root;
    //然后更新当前节点的高度
    update_height(root);
    //更新右孩子的高度
    update_height(new_node);
    //其他节点的高度是没有改变的
    //因为右孩子替代了当前节点的位置
    //那么就返回右孩子
    return new_node;
}

//右旋操作
Node *right_rotate(Node *root) {
    //右旋操作同理反过来思考就可以了
    printf("right rotate : %d\n", root->key);
    Node *new_node = root->lchild;
    root->lchild = new_node->rchild;
    new_node->rchild = root;
    update_height(root);
    update_height(new_node);
    return new_node;
}

const char *type_str[5] = {
    "",
    "maintain type : LL",
    "maintain type : LR",
    "maintain type : RR",
    "maintain type : RL"
};

//平衡操作，也就是判断是LL,RR或者LR和RL类型
//然后再进行左右旋后平衡二叉树
Node *maintain(Node *root) {
    //判断当前子树是否左右子树平衡
    if (abs(H(L(root)) - H(R(root))) <= 1) return root;
    //这里的type只是起了最终演示的效果，用来进行debug和演示的
    int type = 0;
    //判断前面的字母,例如LR中的L
    if (H(L(root)) > H(R(root))) {
        //进入到这里说明是L？类型
        //下面if判断就是是否是LR类型，如果是先进行左旋
        if (H(R(L(root))) > H(L(L(root)))) {
            //说明是LR类型，那么先对当前节点的左子树进行左旋变为LL类型
            //下面会一起对LL类型进行处理
            root->lchild = left_rotate(root->lchild);
            type += 1;
        }
        //因为通过上面的if判断后，如果是LR类型，已经通过左旋变为LL类型
        //如果是LL类型那么上面的if里面的代码段也不会执行
        //所以这里直接右旋处理LL类型，将当前节点进行平衡
        root = right_rotate(root);
        type += 1;
    
    } 
    //这里就是前面字母是R类型了
    else {
        type = 2;
        //if判断是否是RL类型
        if (H(L(R(root))) > H(R(R(root)))) {
            //说明是RL类型，那么先将当前节点的右子树进行右旋
            root->rchild = right_rotate(root->rchild);
            type += 1;
        }
        //对于RR类型处理
        root = left_rotate(root);
        type += 1;
    }
    printf("%s\n", type_str[type]);
    //完成当前节点的平衡操作，返回
    return root;
}

Node *insert(Node *root, int key) {
    //正常的二叉排序节点插入操作
    if (root == NIL) return getNewNode(key);
    if (root->key == key) return root;
    if (key < root->key) root->lchild = insert(root->lchild, key);
    else root->rchild = insert(root->rchild, key);
    //这是一个回溯的过程，所以是从下往上节点进行的下面的操作
    //更新每个节点的高度
    update_height(root);
    //返回平衡后的节点
    return maintain(root);
}

Node *predecessor(Node *root) {
    Node *temp = root->lchild;
    while (temp->rchild != NIL) temp = temp->rchild;
    return temp;
}

Node *erase(Node *root, int key) {
    //删除节点的操作和平衡二叉树一样
    if (root == NIL) return root;
    if (key < root->key) root->lchild = erase(root->lchild, key);
    else if (key > root->key) root->rchild = erase(root->rchild, key);
    else {
        if (root->lchild == NIL || root->rchild == NIL) {
            Node *temp = root->lchild != NIL ? root->lchild : root->rchild;
            free(root);
            return temp;
        } else {
            Node *temp = predecessor(root);
            root->key = temp->key;
            root->lchild = erase(root->lchild, temp->key);
        }
    }
    //然后主要的就是更新高度和平衡操作
    update_height(root);
    return maintain(root);
}

Node *find(Node *root, int key) {
    if (root == NIL) return NIL;
    if (root->key == key) return root;
    if (key < root->key) return find(root->lchild, key);
    return find(root->rchild, key);
}

//清除操作
void clear(Node *root) {
    if (root == NIL) return ;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

void output(Node *root) {
    if (root == NIL) return ;
    printf("(%d[%d] | %d, %d)\n", 
        K(root), H(root), 
        K(L(root)), K(R(root))
    );
    output(root->lchild);
    output(root->rchild);
    return ;
}

int main() {
    srand(time(0));
    Node *root = NIL;
    int x;
    // insert
    while (~scanf("%d", &x)) {
        if (x == -1) break;
        printf("insert %d to avl tree\n", x);
        root = insert(root, x);
        output(root);
    }
    // erase
    while (~scanf("%d", &x)) {
        if (x == -1) break;
        printf("erase %d from avl tree\n", x);
        root = erase(root, x);
        output(root);
    }
    // find
    while (~scanf("%d", &x)) {
        if (x == -1) break;
        printf("find %d in avl : %d\n", x, find(root, x) != NIL);
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1713660.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

便携式应急气象站：应急气象监测装备

便携式应急气象站：应急气象监测装备

TH-BQX5便携式应急气象站&#xff0c;作为现代气象监测的重要装备&#xff0c;以其独特的便携性、高效性和灵活性&#xff0c;在应急气象监测领域发挥着至关重要的作用。这类气象站不仅为灾害预警、环境保护、农业生产等多个领域提供了实时、准确的气象数据&#xff0c;还在突发…
阅读更多...
uniapp通过Canvas绘制网格（心电图，坐标纸等可用）

uniapp通过Canvas绘制网格（心电图，坐标纸等可用）

本篇文档是Canvas绘制心电图的第一个部分&#xff0c;想了解详情的可以关注后学习交流。 心电图的最底层需要一个网状底层&#xff0c;来方便进行数据的测量。 一、白底分大、中、小三个区域的网格 1、首先是HTML部分 <!DOCTYPE html> <html lang"en">…
阅读更多...
DNS设置(linux)

DNS设置(linux)

1.配置dns需要现在/etc/sysconfig/network-scripts/目录下的ifcfg-ens33(后面数字也可能是其他的)中配置DNS 2.编辑/etc/resolv.conf文件&#xff0c;将上面网卡中加的dns服务器ip添加到此文件 vi /etc/resolv.conf重启网络配置 service network restart常用的dns的ip 国内…
阅读更多...
qt中实现多语言功能

qt中实现多语言功能

qt中实现多语言功能 原理&#xff1a; 其本质就是生成ts文件&#xff0c;然后使用Linguist软件手工翻译&#xff0c;再生成qm文件&#xff0c;最后在主程序的开始加载不同的qm文件&#xff0c;实现多语言。 步骤&#xff1a; 修改程序文件 在pro文件中加入说明 TRANSLATI…
阅读更多...
通讯录恢复怎么办？保护珍贵联系信息的2个必备技能！

通讯录恢复怎么办？保护珍贵联系信息的2个必备技能！

手机通讯录扮演着重要的角色&#xff0c;它不仅仅是一个简单的联系方式列表&#xff0c;更是我们与亲朋好友、同事、业务伙伴等之间关系的见证。万一不慎丢失或误删通讯录&#xff0c;学会通讯录恢复的技能变得非常重要。本文将为你介绍几种保护珍贵联系信息的必备技能&#xf…
阅读更多...
这样写代码太优雅了吧

这样写代码太优雅了吧

文章目录 优化案例初次优化再次优化看看Spring源码的处理 优化案例 假设一个场景&#xff0c; 开发代码时&#xff0c;需要对类中的方法进行遍历&#xff0c;判断有没有注解NotNull&#xff0c;暂时没有合适的工具类&#xff0c;需要自己手搓一个。 无须多想&#xff0c;分分钟…
阅读更多...
从GPT-3.5到GPT-4O：探索AI的进化之旅，哪一版更懂你？

从GPT-3.5到GPT-4O：探索AI的进化之旅，哪一版更懂你？

如何评价GPT-4o? 最新的GPT-4O&#xff0c;被誉为GPT-4的增强版。它在保持前代产品优秀性能的基础上&#xff0c;大幅降低了使用成本&#xff0c;使得更多的普通用户也能享受到顶尖AI的服务。GPT-4O在非英语语言处理上的强化&#xff0c;更是让其在全球范围内的适用性大大提高…
阅读更多...
使用Java和XxlCrawler获取各城市月度天气情况实践

使用Java和XxlCrawler获取各城市月度天气情况实践

目录 前言 一、历史数据获取 1、关于天气后报 2、信息界面分析 二、数据的提取开发 1、PageVo的定义 2、属性定义 3、实际信息抓取 三、信息抓取调试以及可能的问题 1、信息获取成果 2、关于超时的问题 四、总结 前言 这篇文章主要来源于一个我们家小朋友的一个作业…
阅读更多...
FreeSwitch视频会议同时支持内网和外网接入

FreeSwitch视频会议同时支持内网和外网接入

我们在使用freeswitch进行视频会议时&#xff0c;之前所有的用户都是通过外网的方式接入&#xff0c;因为fs给其返回的sdp协议内容里&#xff0c;只需要fs配置的外网IP就可以了&#xff1b;最近由于引入新的业务需要有其他内网的服务器也可以直接接入fs的视频会议房间&#xff…
阅读更多...
【Spring Cloud】分布式配置

【Spring Cloud】分布式配置

目录 未来的开发场景为什么需要配置中心配置实时生效配置管理流程 开源配置中心基本介绍DisconfSpring Cloud ConfigApolloNacos Spring Cloud Config介绍配置管理工具体系 案例需求编写 Config Server1.创建配置文件2.创建项目3.添加依赖4.添加注解5.修改配置文件application.…
阅读更多...
玩游戏也能学好 JavaScript 啦？

玩游戏也能学好 JavaScript 啦？

最近有朋友问&#xff0c;应该如何学好 JavaScript。不过我做了好多年的后端开发&#xff0c;JavaScript 虽然也是有所接触&#xff0c;但肯定是谈不上精通。在将朋友介绍给公司的前端大神之后&#xff0c;突然想到&#xff0c;学习编程本身还是一个挺枯燥的事情&#xff0c;如…
阅读更多...
FDW（Foreign Data Wrapper）

FDW（Foreign Data Wrapper）

在上一篇博客里&#xff0c;最末尾提到了 FDW。 FDW 到底是什么呢&#xff1f; 标准 FDW&#xff08;Foreign Data Wrapper&#xff09;遵循了 SQL/MED 标准&#xff0c;标准全称&#xff1a;ISO/IEC 9075-9 Management of External Data (SQL/MED) 2003 年&#xff0c;SQL…
阅读更多...
【大数据】Hadoop 2.X和1.X升级优化对比

【大数据】Hadoop 2.X和1.X升级优化对比

目录 1.前言 2.hadoop 1.X的缺点和优化方向 3.解决NameNode的局限性 3.1.Hadoop HA 3.2.Haddop federation 4.yarn 5.周边组件 1.前言 本文是作者大数据系列中的一文&#xff0c;专栏地址&#xff1a; https://blog.csdn.net/joker_zjn/category_12631789.html?spm10…
阅读更多...
相机系列——相机标定简述

相机系列——相机标定简述

作者&#xff1a;木一 对相机系列感兴趣还可看前文了解更多相关内容&#xff1a; 相机系列——透视投影&#xff1a;针孔相机模型 VR/AR/XR背后的逻辑&#xff1f;离不开三维引擎相机 引言 上文我们介绍了针孔相机模型&#xff0c;用来描述相机的透视投影成像过程&#xf…
阅读更多...
数据要素的大海，如何流向千行百业？

数据要素的大海，如何流向千行百业？

文&#xff5c;白 鸽 编&#xff5c;王一粟 当数智化的风吹向银行业&#xff0c;是从底层数据的融合开始的。 在银行风控场景中&#xff0c;一个人想要进行风险投资或借贷&#xff0c;银行往往会评估这个人的信贷和风控策略。在以往的办理模式中&#xff0c;会需要办理人…
阅读更多...
看看最新的B端登录界面，你是不是被潮流抛弃了？

看看最新的B端登录界面，你是不是被潮流抛弃了？

毛玻璃风格&#xff08;Frosted Glass Style&#xff09;是新拟态设计风格中的一种分支&#xff0c;它灵感来源于现实世界中的毛玻璃材质。毛玻璃是一种通过在玻璃表面加工处理的方式&#xff0c;使其具有模糊、云翳和透明效果的特殊玻璃。 在设计中&#xff0c;毛玻璃风格通常…
阅读更多...
OrangePi Kunpeng Pro体验——安装Hass与驱动SPI小屏幕

OrangePi Kunpeng Pro体验——安装Hass与驱动SPI小屏幕

OrangePi Kunpeng Pro 是一款面向开发者和爱好者的高性能开发板。在本次测评中&#xff0c;主要将以前的一些代码在该开发板上实现&#xff0c;包括docker部署hass&#xff0c;引脚驱动SPI小屏幕。中间遇到了一些小小问题&#xff0c;但都成功了&#xff0c;一起来试试吧~ 一、…
阅读更多...
NoSQL是什么？NoSQL数据库存在SQL注入攻击?

NoSQL是什么？NoSQL数据库存在SQL注入攻击?

一、NoSQL是什么&#xff1f; NoSQL&#xff08;Not Only SQL&#xff09;是一种非关系型数据库的概念。与传统的关系型数据库不同&#xff0c;NoSQL数据库使用不同的数据模型来存储和检索数据。NOSQL数据库通常更适合处理大规模的非结构化和半结构化数据&#xff0c;且能够…
阅读更多...
n后问题 回溯笔记

n后问题 回溯笔记

问题描述 在nn格的棋盘上放置彼此不受攻击的n个皇后。 按照国际象棋的规则&#xff0c;皇后可以攻击与之处在同 一行或同一列或同一斜线上的棋子。n后问题等价于在nn格的棋盘上放置n个皇后&#xff0c;任何2个皇后不放在同一行或同一列或同一斜线上。 代码 import java.uti…
阅读更多...
史上最全排序算法整理！（1）

史上最全排序算法整理！（1）

1.排序的概念及其应用 1.1排序的概念 排序是计算机内经常进行的一种操作&#xff0c;其目的是将一组“无序”的记录序列调整为“有序”的记录序列。分内部排序和外部排序&#xff0c;若整个排序过程不需要访问外存便能完成&#xff0c;则称此类排序问题为内部排序。反之&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023