代码随想录算法训练营Day 53| 动态规划part14 | 1143.最长公共子序列、1035.不相交的线 、53. 最大子序和 （动态规划 ）

---

---

1143.最长公共子序列

题目链接

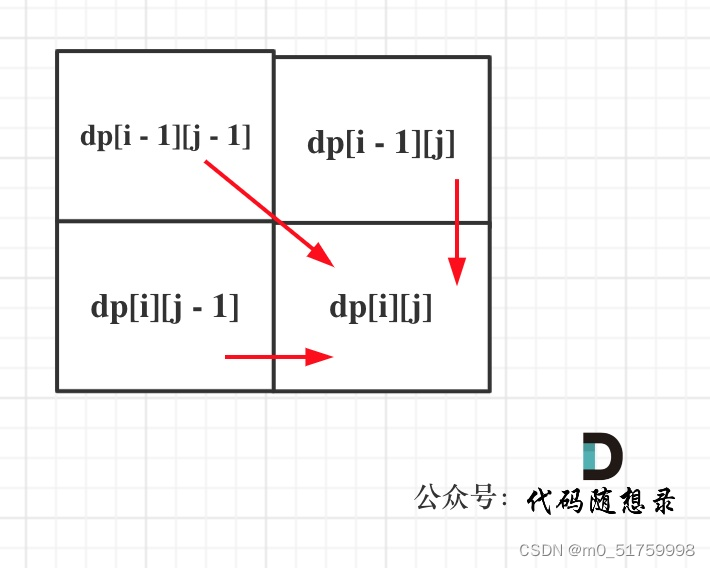
一、二维DP

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        """
        :type text1: str
        :type text2: str
        :rtype: int
        """
        # dp[i][j]表示text1[i-1]和text2[j-1]的最长公共子序列长度
        dp=[[0]*(1+len(text2)) for _ in range(len(text1)+1)]
 
        for i in range(1,len(text1)+1):
            for j in range(1,len(text2)+1):
                if text1[i-1]==text2[j-1]:
                    dp[i][j]=dp[i-1][j-1]+1
                else:
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1])
        return dp[-1][-1]

二、一维DP

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m, n = len(text1), len(text2)
        dp = [0] * (n + 1)  # 初始化一维DP数组
        
        for i in range(1, m + 1):
            prev = 0  # 保存上一个位置的最长公共子序列长度
            for j in range(1, n + 1):
                curr = dp[j]  # 保存当前位置的最长公共子序列长度
                if text1[i - 1] == text2[j - 1]:
                    # 如果当前字符相等，则最长公共子序列长度加一
                    dp[j] = prev + 1
                else:
                    # 如果当前字符不相等，则选择保留前一个位置的最长公共子序列长度中的较大值
                    dp[j] = max(dp[j], dp[j - 1])
                prev = curr  # 更新上一个位置的最长公共子序列长度
        
        return dp[n]  # 返回最后一个位置的最长公共子序列长度作为结果

---

1035.不相交的线

题目链接

一、同上一题

class Solution(object):
    def maxUncrossedLines(self, nums1, nums2):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :rtype: int
        """
        # 同最长公共子序列
        dp=[[0]*(len(nums2)+1) for _ in range(len(nums1)+1)]
        for i in range(1,len(nums1)+1):
            for j in range(1,len(nums2)+1):
                if nums1[i-1]==nums2[j-1]:
                    dp[i][j]=dp[i-1][j-1]+1
                else:
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1])
        return dp[-1][-1]

---

53. 最大子数组和

题目链接

一、动态规划

class Solution(object):
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        # 动态规划
        # dp[i] 到nums[i-1]的最大子数组和
        dp=[0]*len(nums)
        dp[0]=nums[0]
        result = dp[0]
        for i in range(1, len(nums)):
            dp[i] = max(dp[i-1] + nums[i], nums[i]) #状态转移公式
            result = max(result, dp[i]) #result 保存dp[i]的最大值
        return result

二、贪心

class Solution(object):
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        # 贪心
        sum = 0
        maxsum = float('-inf')
        # 遇到加和为负数 直接从下一个数开始count
        for i in range(len(nums)):    
            if sum <0:
                sum = nums[i]  
            else:
                sum +=nums[i]   
            if maxsum < sum:
                maxsum = max(maxsum, sum)   
        return maxsum