树--搜索二叉树

news2024/11/18 11:33:52

现有一棵结点数目为n的二叉树，采用二叉链表的形式存储。对于每个结点均有指向左右孩子的两个指针域，而结点为n的二叉树一共有n-1条有效分支路径。那么，则二叉链表中存在2n-(n-1)=n+1个空指针域。那么，这些空指针造成了空间浪费。

例如：图2.1所示一棵二叉树一共有10个结点，空指针^有11个。

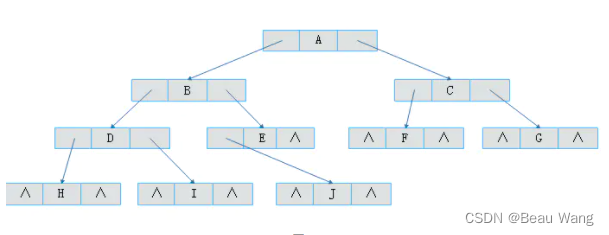
此外，当对二叉树进行中序遍历时可以得到二叉树的中序序列。例如：图2.1所示二叉树的中序遍历结果为HDIBJEAFCG，可以得知A的前驱结点为E，后继结点为F。但是，这种关系的获得是建立在完成遍历后得到的，那么可不可以在建立二叉树时就记录下前驱后继的关系呢，那么在后续寻找前驱结点和后继结点时将大大提升效率。

线索化

现将某结点的空指针域指向该结点的前驱后继，定义规则如下：

若结点的左子树为空，则该结点的左孩子指针指向其前驱结点。

若结点的右子树为空，则该结点的右孩子指针指向其后继结点。

这种指向前驱和后继的指针称为线索。将一棵普通二叉树以某种次序遍历，并添加线索的过程称为线索化。

按照规则将图2.1所示二叉树线索化后如图所示：

图中黑色点画线为指向后继的线索，紫色虚线为指向前驱的线索。

可以看出通过线索化，既解决了空间浪费问题，又解决了前驱后继的记录问题。

线索化带来新问题

可以将一棵二叉树线索化为一棵线索二叉树，那么新的问题产生了。我们如何区分一个结点的lchild指针是指向左孩子还是前驱结点呢？例如：对于图所示的结点E，如何区分其lchild的指向的结点J是其左孩子还是前驱结点呢？

为了解决这一问题，现需要添加标志位ltag，rtag。并定义规则如下：

ltag为0时，指向左孩子，为1时指向前驱

rtag为0时，指向右孩子，为1时指向后继

添加ltag和rtag属性后的结点结构如下：

上图所示线索二叉树转变为图所示的二叉树。

题

答案：b

线索二叉树结点数据结构

//#define Link 0//指针标志  
//#define Thread 1//线索标志  
typedef char TElemType;   
//中序线索二叉树  
typedef enum PointerTag {Link, Thread};//结点的child域类型，link表示是指针，指向孩子结点，thread表示是线索，指示前驱或后继结点  
//定义结点数据结构
typedef struct ThrBiNode{  
    TElemType data;  
    ThrBiNode *lchild, *rchild;//左右孩子指针  
    PointerTag lTag, rTag;//左右标志  
}ThrBiNode, *ThrBiTree;

中序遍历建立线索二叉树

中序遍历的方法已经在第一篇二叉基础树中讲解过，那么实现线索化的过程就是在中序遍历同时修改结点空指针的指向。

采用中序遍历的访问顺序实现一棵二叉树的线索化过程代码如下：

//中序遍历进行中序线索化
void inThreading(ThrBiTree T, ThrBiTree &pre){  
    if(T){  
        inThreading(T->lchild, pre);//左子树线索化  
  
        if(!T->lchild){//当前结点的左孩子为空  
            T->lTag = Thread;  
            T->lchild = pre;  
        }else{  
            T->lTag = Link;  
        }  
  
        if(!pre->rchild){//前驱结点的右孩子为空  
            pre->rTag = Thread;  
            pre->rchild = T;  
        }else{  
            pre->rTag = Link;  
        }  
        pre = T;          
        inThreading(T->rchild, pre);//右子树线索化  
    }  
}

加上头结点，遍历线索二叉树

加上线索的二叉树结构是一个双向链表结构，为了便于遍历线索二叉树，我们为其添加一个头结点，头结点左孩子指向原二叉树的根结点，右孩子指针指向中序遍历的最后一个结点。同时，将第一个结点左孩子指针指向头结点，最后一个结点的右孩子指针指向头结点。

上图所示线索二叉树添加头结点后如图所示：

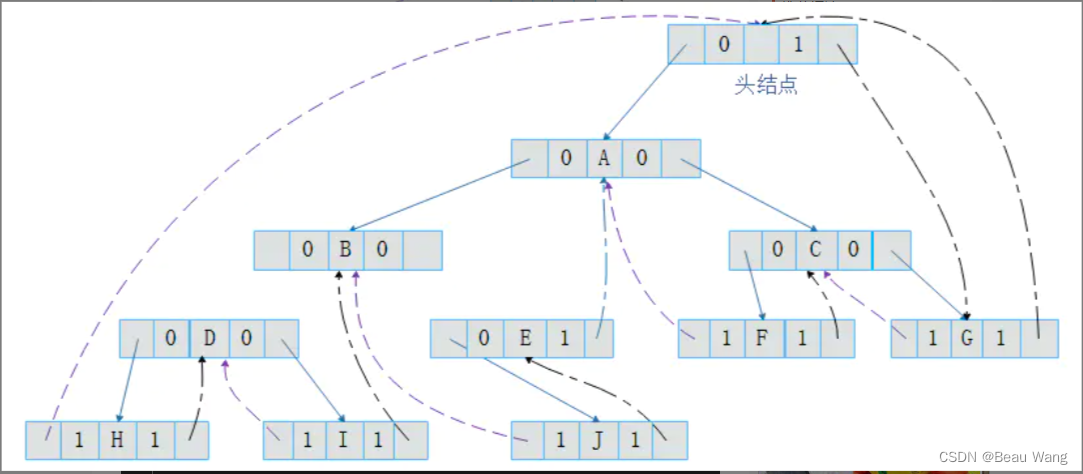
带有头结点的线索二叉树遍历代码如下：

//T指向头结点，头结点的lchild链域指针指向二叉树的根结点  
//中序遍历打印二叉线索树T（非递归算法）  
void inOrderTraversePrint(ThrBiTree T){  
    ThrBiNode *p = T->lchild;//p指向根结点  
      
    while(p != T){//空树或遍历结束时，p == T  
        while(p->lTag == Link){  
            p = p->lchild;  
        }  
        //此时p指向中序遍历序列的第一个结点（最左下的结点）  
  
        printf("%c ", p->data);//打印（访问）其左子树为空的结点  
  
        while(p->rTag == Thread && p->rchild != T){  
            p = p->rchild;  
            printf("%c ", p->data);//访问后继结点  
        }  
        //当p所指结点的rchild指向的是孩子结点而不是线索时，p的后继应该是其右子树的最左下的结点，即遍历其右子树时访问的第一个节点  
        p = p->rchild;  
    }  
    printf("\n");  
}