Sklearn中与特征缩放有关的五个函数和类，全部位于sklearn.preprocessing包内。作为一个系列文章，我们将逐一讲解Sklearn中提供的标准化和归一化方法，以下是本系列已发布的文章列表：

Sklearn标准化和归一化方法汇总(1)：标准化 / 标准差归一化 / Z-Score归一化
Sklearn标准化和归一化方法汇总(2)：Min-Max归一化
Sklearn标准化和归一化方法汇总(3)：范数归一化

以下是Sklearn中的五种与特征缩放相关的函数和类，我们的研究也是为围绕这些函数和类展开的：

名称	方法名	类名
标准化 / Z-Score 归一化 / 标准差归一化	sklearn.preprocessing.scale	sklearn.preprocessing.StandardScaler
Min-Max 归一化	sklearn.preprocessing.minmax_scale	sklearn.preprocessing.MinMaxScaler
范数归一化	sklearn.preprocessing.normalize	sklearn.preprocessing.Normalizer
Robust Scaler（无常用别名）	sklearn.preprocessing.robust_scale	sklearn.preprocessing.RobustScaler
Power Transformer （无常用别名）	sklearn.preprocessing.power_transform	sklearn.preprocessing.PowerTransformer

关于各种关于标准化和归一化的概念和分类，我们已经在此前一篇文章《标准化和归一化概念澄清与梳理》中做了详细的梳理和澄清，不清楚的读者可以先阅读一下此文。本文我们研究第三种归一化手段：范数归一化。本文地址：https://laurence.blog.csdn.net/article/details/128723321，转载请注明出处！

1. 算法

范数归一化的计算逻辑是：先计算出一个向量（通常是一行）的范数（如无特殊说明，通常都是指L-2范数），然后让向量中的每一个元素除以这个范数，得到的新向量就是范数归一化后的结果。所以，理解范数归一化的关键是要理解：范数。我们已经在此前一篇文章中专门做了介绍，请参考《范数的意义与计算方法》一文。

由于范数表示一个向量的“长度”，一个向量除以了自己的“范数”后，就等于把自己的“长度”缩放成了单位长度：1，所以可以想象：在一个二维的向量空间中，范数为1的向量都会分布在以原点为圆心，半径为1的圆上，如果是三维的向量空间，会分布在以原点为圆心，半径为1的圆球上。。

范数归一化与此前介绍的标准差归一化和Min-Max归一化有本质的不同，它是面向向量或矩阵的，所以默认也是按行（即向量形式）进行运算的。应用范数归一化的前提是：当前操作的多维数组是一个有意义的向量或矩阵，或者说是需要准备拿它去进行向量或矩阵运算（这在机器学习算法中很常见），在此前提下，当我们使用范数归一化时，是将一个向量（通常是二维数组中的一行）作为一个整体去运算的，通俗地说就是：此时的一行数据才是一个数（一个向量）。

“范数归一化是应用在向量（或矩阵）上”这一点也体现在了API层面上，第一点是：你可能会发现像scale()和minmax_scale()这类归一化函数还可以接受一维数组，但到了normalize()就不会再接受一维数组了，需要至少要二维以上的数组（否则会报“Expected 2D array, got 1D array instead”错误），这在暗示：针对一维数组（非向量）应用范数归一化是无意义的；第二点是：像scale()和minmax_scale()这类归一化函数默认是“列”向操作，而normalize()默认则是“行”向操作，这在暗示它是操作向量的，这都是根据它的实际应用场景设置的默认参数，所以能反映出它的一些本质特征。

总结一下：范数归一化是面向向量（或矩阵）的运算，所以默认也是按行（即向量形式）进行处理。

2. 示例

2.1 一个“无意义”的示例

有很多刚接触范数归一化的人会沿袭对其他归一化方法的理解来试图理解范数归一化，包括使用的测试数据也是一样的单列数据，就如同我们在本系列前面两篇文章中使用到的身高数据一样，于是，在初学者那里我们会常常看到类似下面的归一化结果以及数据分布图，我们要说的是：虽然计算上没有错误，但这种处理是没有意义的，也就不会出现在实际应用中，因为我们试图处理的数据根本不是一个有意义的向量数据，所以处理结果也是无意义的。那就让我们使用此前的身高数据看一下非向量（一维数组）到底会被处理成什么样子：

# 范数归一化 (在非向量上的无意义应用）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import Normalizer
from sklearn.preprocessing import normalize
# author: https://laurence.blog.csdn.net/

%matplotlib inline
np.random.seed(42)
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(13,5))

heights = np.random.normal(loc=170, scale=170*0.15, size=1000)
print("1. 原始数据")
print(f"heights (first 3 elements) = {heights[:3]}")

# 不同于scale()和minmax_scale()还能接受一维数组，normalize()已不接受一维数组了，至少要二维以上。
# 否则就会报错：Expected 2D array, got 1D array instead, 这暗示：范数归一化是面向向量或整个矩阵的
# 所以从API层面就作出了限制，因此我必须一开始将heights转置为二维（单列）数组
heights = heights.reshape(-1,1)
print(f"reshaped heights (first 3 elements) = {heights[:3].tolist()}")

ax1.hist(heights, bins=50)
ax1.set_title("raw data")
ax1.annotate(f"σ = {heights.std()}", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

print("--------------------------------------------------------------------------------------------------------------")

print("2. 使用normalize按行进”行“范数归一化")
# 不指定axis参数，默认也是按行, 这也体现了normalize是面向向量运算的设计意图
normalized_heights = normalize(heights, axis=1)
print(f"normalized_heights(first 3 elements) = {normalized_heights[:3, :].tolist()}")
ax2.hist(normalized_heights, bins=50)
ax2.set_title("normalize() by row")
ax2.annotate(f"σ = {normalized_heights.std()}", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

print("--------------------------------------------------------------------------------------------------------------")

print("3. 使用normalize按”列“进行范数归一化")
# 列向操作并不是normalize的默认操作轴向，必须显式设置！
normalized_heights = normalize(heights, axis=0)
print(f"normalized_heights(first 3 elements) = {normalized_heights[:3, :].tolist()}")
ax3.hist(normalized_heights, bins=50)
ax3.set_title("normalize() by col")
ax3.annotate(f"σ = {normalized_heights.std()}", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

print("--------------------------------------------------------------------------------------------------------------")

print("4. 使用Normalizer进行范数归一化")
# Normalizer不可设置轴向，只能按“行”
normalized_heights = Normalizer().fit_transform(heights)
print(f"normalized_heights(first 3 elements) = {normalized_heights[:3, :].tolist()}")
ax4.hist(normalized_heights, bins=50)
ax4.set_title("Normalizer")
ax4.annotate(f"σ = {normalized_heights.std()}", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

plt.show()

输出数据：

1. 原始数据
heights (first 3 elements) = [182.6662109  166.47426032 186.51605772]
reshaped heights (first 3 elements) = [[182.66621090178643], [166.4742603201348], [186.51605772156765]]
--------------------------------------------------------------------------------------------------------------
2. 使用normalize按行进”行“范数归一化
normalized_heights(first 3 elements) = [[1.0], [1.0], [1.0]]
--------------------------------------------------------------------------------------------------------------
3. 使用normalize按”列“进行范数归一化
normalized_heights(first 3 elements) = [[0.03352337883141376], [0.030551789884073692], [0.03422991274781404]]
--------------------------------------------------------------------------------------------------------------
4. 使用Normalizer进行范数归一化
normalized_heights(first 3 elements) = [[1.0], [1.0], [1.0]]

输出图表：

在这里插入图片描述

现在我们来解读一下程序输出的数据和图表。我们准备的身高数据并不是一个向量，在还没有认识到这个问题的情况下，为了能够进行范数归一化，我们把它强行转置为一个二维（单列）数组：

[[182.66621090178643], 
 [166.47426032013480], 
 [186.51605772156765],
 ...
 [165.84179242457762]]

在此基础上，我们有两种选择，也是看待数据的两种方式：

按“行”范数归一化

如果我们打算按“行”进行范数归一化，则每一行会被视为一个向量，由于我们的数据一行只有一个元素，即一个向量只有一个分量，套用范数归一化的计算公式可知，不管是什么值，计算出的结果都为1，所以1000行数据就被转置为了：

[[1.0], 
 [1.0], 
 [1.0],
 ...
 [1.0]]

此时数据分布就变为图中第2和第4两个子图的样子，这种转换毫无意义。

按“列”范数归一化

如果我们打算按“列”进行范数归一化，则每一列会被视为一个向量，此时，我们只有一个向量，这个向量包含1000个维度的分量，经归一化处理后，得到的结果是：

[[0.03352337883141376], 
 [0.030551789884073692], 
 [0.03422991274781404],
 ...
 [0.03123451354323424]]

对应的数据分布就是图3所示的样子，看上去已经“有那味”了，数据被缩放了，分布还保持与原始数据一样，很多介绍范数的文章就到此结束了。然而实际的情况是：这个由1000个身高数据组成的向量是一个“怪物”，根本不是一个有意义的向量，完全体现不出范数归一化的作用。

2.2 一个“有意义”的示例

由于我们准备的身高数据不是一组有意义的向量，这导致上面的示例不管是按行还是按列，都无法展示范数归一化的真正效果，问题的关键就是：身高数据是一个单维数据，我们需要准备至少包含两个维度的向量来演示范数归一化，才能看到它的转换效果。所以，我们应该再引入一个维度：体重，组成一个由身高和体重构成的二维向量，然后对其进行范数归一化：

# 范数归一化 (在向量上的有意义应用）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import normalize
from sklearn.preprocessing import StandardScaler
# author: https://laurence.blog.csdn.net/

%matplotlib inline
np.random.seed(42)
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15,5))

# 我们不能再用身高数据演示范数归一化了，因为从数据的意义上讲它是一”列“数据，而范数归一化是面向向量（或矩阵）的，也就是一行数据
# 如果我们把这组身高数据当成”行“进行范数归一化，可以计算，但没有任何意义，因为这组数据不是一个向量；
# 如果我们把这组身高数据当成”列“进行范数归一化，则每一行只有一个元素，所以归一化的结果是：所有的身高数据都被缩放成了1，这也没有意义

# 使用有意义的二维向量
heights_weights = np.random.normal(loc=(170, 60), scale=(170*0.15, 60*0.15), size=(1000, 2))

print("1. 原始数据")
print(f"heights_weights (first 2 elements) = {heights_weights[:2, :].tolist()}")
ax1.scatter(x=heights_weights[:,0], y=heights_weights[:,1])
ax1.set_title("raw data")

print("-------------------------------------------------------------------------------------------------------------------------------------")

print("2. 使用normalize范数归一化")
# 默认按行向量进行范数归一化，也符合我们的期望，针对本数据按“列”无意义，不演示
normalized_heights_weights = normalize(heights_weights)
print(f"normalized_heights_weights (first 2 elements) = {normalized_heights_weights[:2, :].tolist()}")
ax2.scatter(x=normalized_heights_weights[:,0], y=normalized_heights_weights[:,1])
ax2.set_title("normalize()")

print("-------------------------------------------------------------------------------------------------------------------------------------")

print("3. 使用Normalizer范数归一化")
# 只能按行向量进行范数归一化，也符合我们的期望，针对本数据按“列”无意义，不演示
normalized_heights_weights = Normalizer().fit_transform(heights_weights)
print(f"normalized_heights_weights (first 2 elements) = {normalized_heights_weights[:2, :].tolist()}")
ax3.scatter(x=normalized_heights_weights[:,0], y=normalized_heights_weights[:,1])
ax3.set_title("Normalizer (center view)")
ax3.set(xlim=(-1, 1),ylim=(-1, 1))
ax3.axvline(x=0, c='grey')
ax3.axhline(y=0, c='grey')

plt.show()

# 调研数据分布变化

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15,5))
ax1.hist(heights_weights, bins=50)
ax1.set_title("raw data")
# 经过范数归一化后，每一行元素（向量分量）除以的范数都是不一样的，所以每一列元素实际上是进行了
# 无规律的缩放，所以如果观察列数据的分布，其经过范数归一化后，分布一定改变了。但这是在用非向量
# 的视角看待数据，使用范数归一化的场景不会受此影响，也不关注这个问题。
ax2.hist(normalized_heights_weights, bins=50)
ax2.set_title("normalize data")

plt.show()

输出数据：

1. 原始数据
heights_weights (first 2 elements) = [[182.66621090178643, 58.75562128945934], [186.51605772156765, 73.70726870767223]]
-------------------------------------------------------------------------------------------------------------------------------------
2. 使用normalize范数归一化
normalized_heights_weights (first 2 elements) = [[0.9519655603640547, 0.30620511406694606], [0.9300146475620354, 0.3675224555317171]]
-------------------------------------------------------------------------------------------------------------------------------------
3. 使用Normalizer范数归一化
normalized_heights_weights (first 2 elements) = [[0.9519655603640547, 0.30620511406694606], [0.9300146475620354, 0.3675224555317171]]

输出图表：

在这里插入图片描述

改用二维向量数据后，我们能就能从图表中发现范数归一化的真正效果。左一图中的每一个点可以视为一个向量，经过范数归一化后，数据呈现出图二的分布状态，所有向量的“长度”（范数）全部变成了1，表现到图表上就是它们被缩放到了以原点为圆心，1为半径的圆上！同时，可以看到正态分布对点位在圆上的分布影响，而图三是为了凸显归一化后数据是分布在单位圆上，特意将坐标系居中显示，从中可以观察到那是单位园上的一小段圆弧。最后，我们再看一下数据分布：

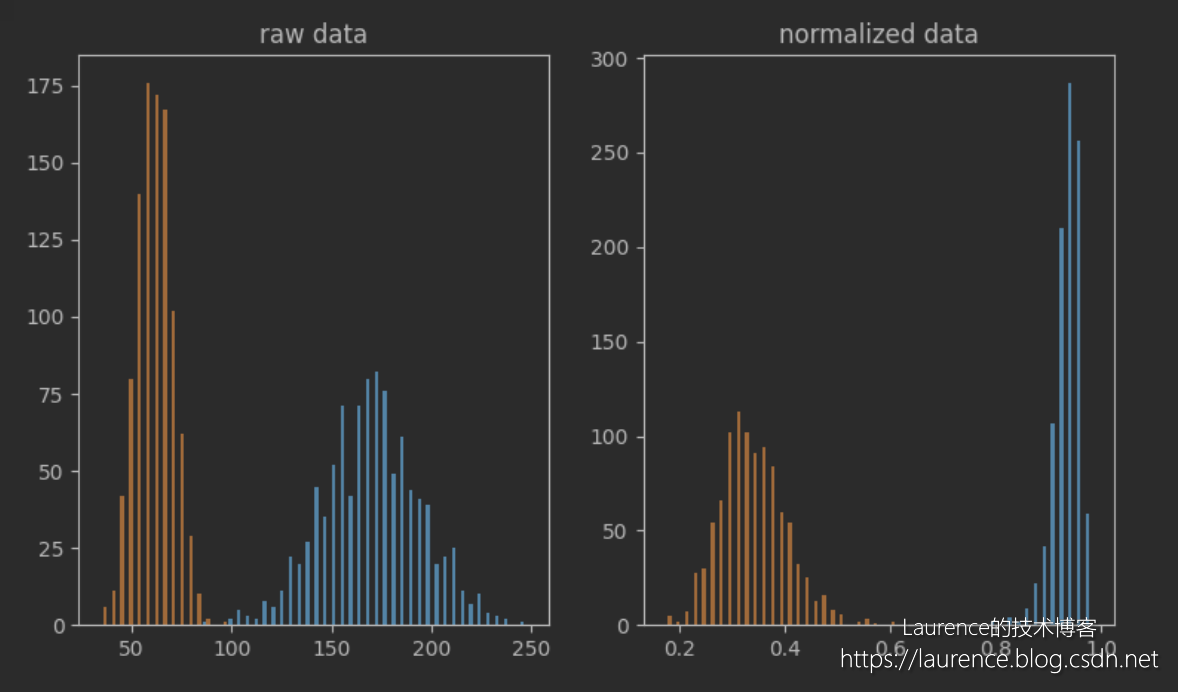
在这里插入图片描述

由于数据是按行处理的，所以从列向角度看，同一个列（例如身高）中的每个元素都除以了不同的数（所在行的范数），所以列的数据分布必然会发生改变，上图显示的非常明显。但同样的道理，因为现在的场景是向量运算，所以也不会考察列向数据的分布。这就是我们在介绍范数归一化时反复强调的：范数归一化和标准差归一化、Min-Max归一化等其他归一化方法是完全不同的缩放手段，它缩放的是向量。