236. 二叉树的最近公共祖先(C++)

news2024/11/17 14:20:04

文章目录

前言
一、题目介绍
二、解决方案
三、优化
总结

前言

在本篇文章中我们将会讲解二叉树中极为经典的题目236. 二叉树的最近公共祖先

一、题目介绍

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：
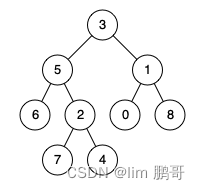
在这里插入图片描述

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2：
在这里插入图片描述

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

我们举几个例子，方便大家更好的理解
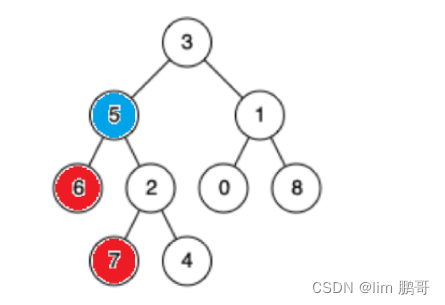
在这里插入图片描述
6和7的公共祖先右5，3，但是题目要求我们找最近公共祖先，也就是5.

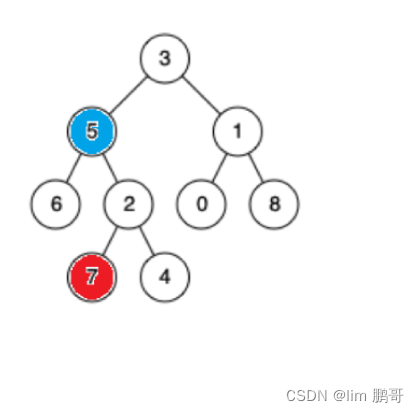
7和5的最近公共祖先是5.

同时注意一下提示：
🌟所有 Node.val 互不相同。
🌟p != q
🌟p 和 q 均存在于给定的二叉树中。

二、解决方案

我们通过分析可以发现这样的规律

一个节点在左子树，一个节点在右子树，这个节点就是最近公共祖先
一个节点是另一个节点的祖先节点，这个祖先节点就是最近公共祖先

我们可以根据这一特性解决这道问题
🌟判断这个节点是不是根节点，如果是我们就返回这个节点。这时这个节点就是另一个节点的祖先
🌟如果两个节点都在左子树，我们就去左子树寻找
🌟如果两个节点都在右子树，我们就去右子树寻找

class Solution {
public:
    bool IsInTree(TreeNode* root, TreeNode* x)
    {
        if (root == nullptr)
        {
            return false;
        }
        //前序遍历
        if (root == x)
        {
            return true;
        }
        if (IsInTree(root->left, x))
        {
            return true;
        }
        if (IsInTree(root->right, x))
        {
            return true;
        }
        return false;
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
    {
        if (root == nullptr)
        {
            return nullptr;
        }
        //判断这个节点
        if (root == p || root == q)
        {
            return root;
        }

        bool pInLeft, pInRight, qInLeft, qInRight;
        pInLeft = IsInTree(root->left, p);
        pInRight = !pInLeft;
        qInLeft = IsInTree(root->left, q);
        qInRight = !qInLeft;
        //一个在左边，一个在右边，root就是最近公共祖先
        if ((pInRight && qInLeft) || (qInRight && pInLeft))
        {
            return root;
        }
        //都在左边，去左子树找
        if (pInLeft && qInLeft)
        {
            return lowestCommonAncestor(root->left, p, q);
        }
        //都在右边，去右子树找
        else if (qInRight && pInRight)
        {
            return lowestCommonAncestor(root->right, p, q);
        }
        //找不到
        return nullptr;
    }
};

我们看一下时间复杂度：
按照最快情况分析
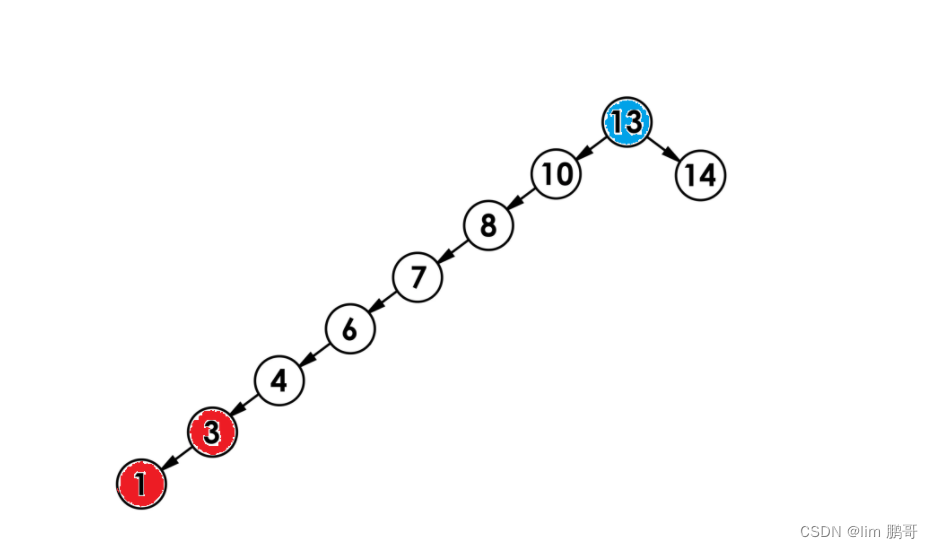
在这里插入图片描述
1和3的最经公共祖先是13.时间复杂度为O（N*2）

我们能否进行优化呢？？？

三、优化

我们还有一种解决方案，如果这个节点存了父亲节点，我们就很容易解决这道问题。
转化为：两个链表找交点

但是这道题目没有父亲节点，我们可以转化成求路径
🌟找出两个节点从根节点到这个节点的路径。
🌟路径长的先走差数次
🌟两个路径一起删除节点，最先相同的就是最近公共祖先。

我们通过上帝视角看一下
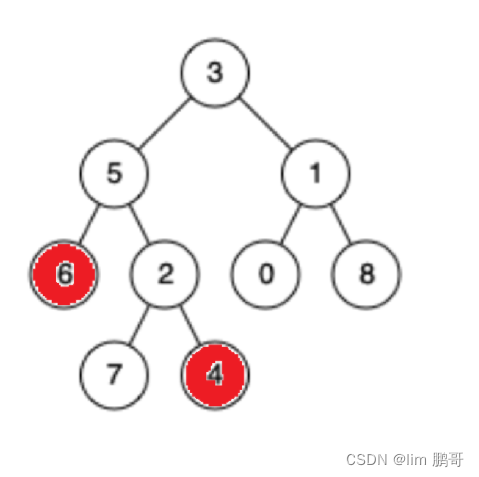
在这里插入图片描述

找到两条路径
在这里插入图片描述
路径长的先走差数次

两个路径一起删除节点，最先相同的就是最近公共祖先

在这里插入图片描述

如何查找两条路径？？借助栈来实现

进行前序遍历
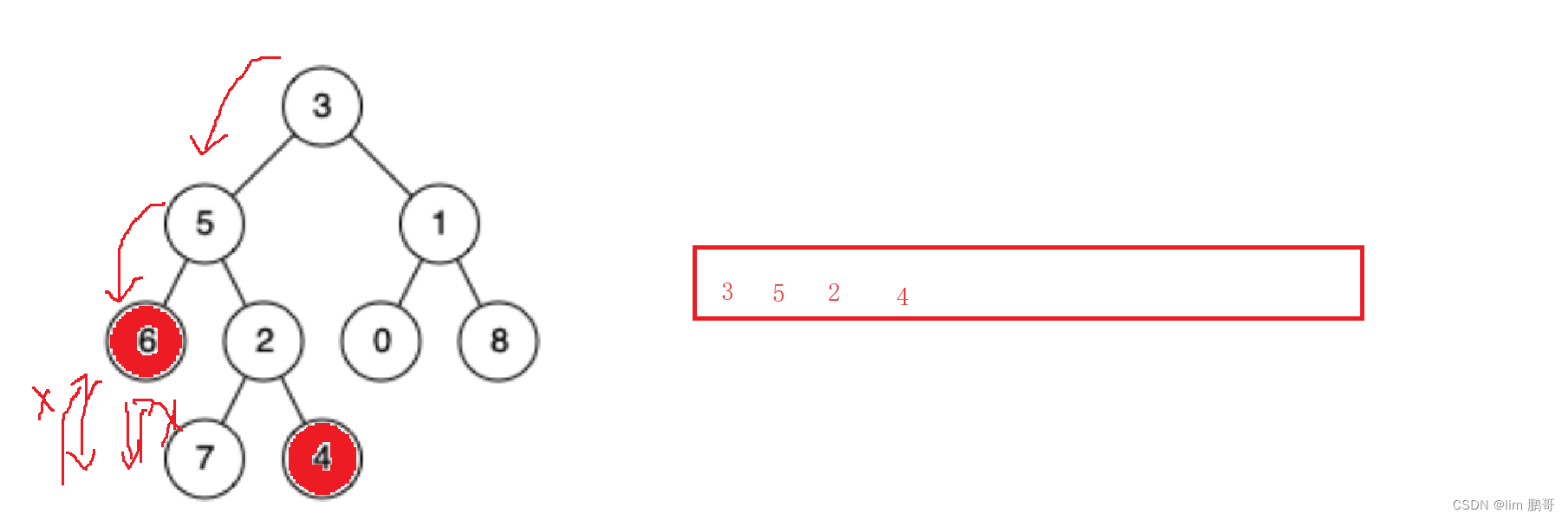
在这里插入图片描述

代码编写

class Solution {
public:
    bool Route(stack<TreeNode*>& s, TreeNode* root, TreeNode* p)
    {
        if (root == nullptr)
        {
            return false;
        }
        //先入栈
        s.push(root);
        //判断这个节点
        if (root == p)
        {
            return true;
        }
        //判断左子树
        if (Route(s, root->left, p))
        {
            return true;
        }
        //判断右子树
        if (Route(s, root->right, p))
        {
            return true;
        }
        //不在左也不再右，从栈里删除这个节点
        s.pop();
        return false;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
    {
        stack<TreeNode*>s1;
        stack<TreeNode*>s2;
        Route(s1, root, p);
        Route(s2, root, q);
        //长的先走
        while (s1.size() != s2.size())
        {
            if (s1.size() > s2.size())
            {
                s1.pop();
            }
            else
            {
                s2.pop();
            }
        }
        //一起走
        while (s1.size())
        {
            //相同
            if (s1.top() == s2.top())
            {
                return s1.top();
            }
            s1.pop();
            s2.pop();
        }
        return nullptr;
    }
};