Python 机器学习 基础 之 无监督学习 【聚类(clustering)/k均值聚类/凝聚聚类/DBSCAN】的简单说明
目录
Python 机器学习 基础 之 无监督学习 【聚类(clustering)/k均值聚类/凝聚聚类/DBSCAN】的简单说明
一、简单介绍
二、聚类(clustering)
附录
一、参考文献
一、简单介绍
Python是一种跨平台的计算机程序设计语言。是一种面向对象的动态类型语言,最初被设计用于编写自动化脚本(shell),随着版本的不断更新和语言新功能的添加,越多被用于独立的、大型项目的开发。Python是一种解释型脚本语言,可以应用于以下领域: Web 和 Internet开发、科学计算和统计、人工智能、教育、桌面界面开发、软件开发、后端开发、网络爬虫。
Python 机器学习是利用 Python 编程语言中的各种工具和库来实现机器学习算法和技术的过程。Python 是一种功能强大且易于学习和使用的编程语言,因此成为了机器学习领域的首选语言之一。Python 提供了丰富的机器学习库,如Scikit-learn、TensorFlow、Keras、PyTorch等,这些库包含了许多常用的机器学习算法和深度学习框架,使得开发者能够快速实现、测试和部署各种机器学习模型。
Python 机器学习涵盖了许多任务和技术,包括但不限于:
- 监督学习:包括分类、回归等任务。
- 无监督学习:如聚类、降维等。
- 半监督学习:结合了有监督和无监督学习的技术。
- 强化学习:通过与环境的交互学习来优化决策策略。
- 深度学习:利用深度神经网络进行学习和预测。
通过 Python 进行机器学习,开发者可以利用其丰富的工具和库来处理数据、构建模型、评估模型性能,并将模型部署到实际应用中。Python 的易用性和庞大的社区支持使得机器学习在各个领域都得到了广泛的应用和发展。
二、聚类(clustering)
我们前面说过,聚类 (clustering)是将数据集划分成组的任务,这些组叫作簇(cluster)。其目标是划分数据,使得一个簇内的数据点非常相似且不同簇内的数据点非常不同。与分类算法类似,聚类算法为每个数据点分配(或预测)一个数字,表示这个点属于哪个簇。
1、k均值聚类
k 均值聚类是最简单也最常用的聚类算法之一。它试图找到代表数据特定区域的簇中心 (cluster center)。算法交替执行以下两个步骤:将每个数据点分配给最近的簇中心,然后将每个簇中心设置为所分配的所有数据点的平均值。如果簇的分配不再发生变化,那么算法结束。下面的例子(图 3-23)在一个模拟数据集上对这一算法进行说明:
import mglearn
import matplotlib.pyplot as plt
mglearn.plots.plot_kmeans_algorithm()
plt.tight_layout()
plt.savefig('Images/03Clustering-01.png', bbox_inches='tight')
plt.show()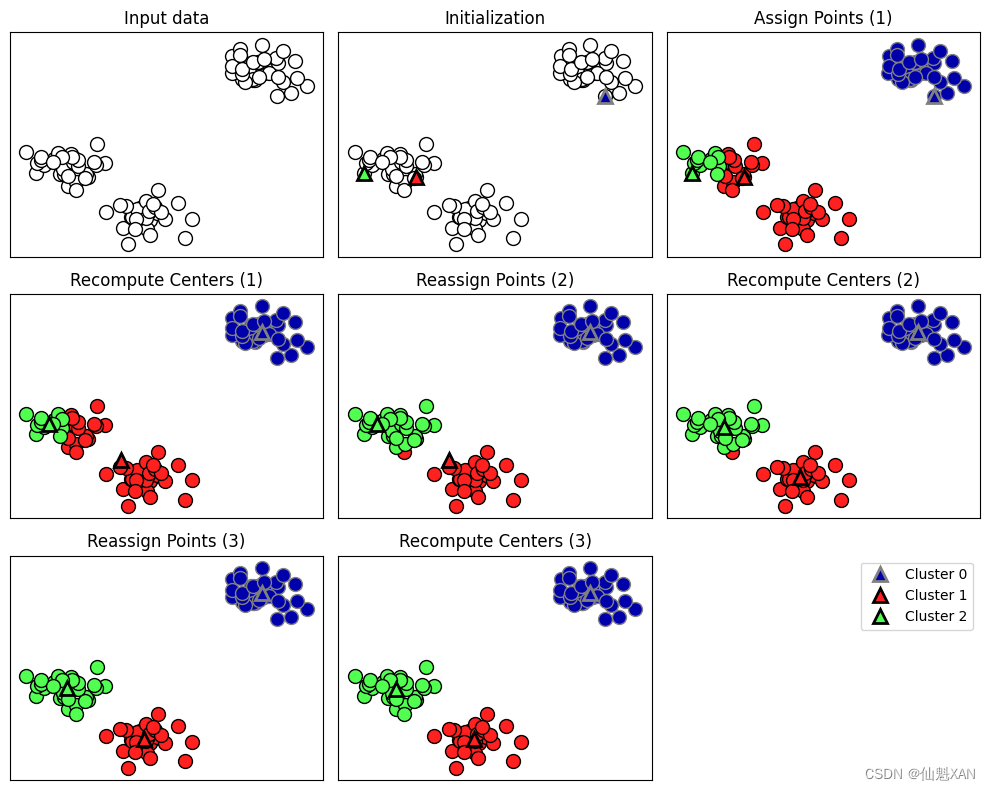
簇中心用三角形表示,而数据点用圆形表示。颜色表示簇成员。我们指定要寻找三个簇,所以通过声明三个随机数据点为簇中心来将算法初始化(见图中“Initialization”/“初始化”)。然后开始迭代算法。首先,每个数据点被分配给距离最近的簇中心(见图中“Assign Points (1)”/“分配数据点(1)”)。接下来,将簇中心修改为所分配点的平均值(见图中“Recompute Centers (1)”/“重新计算中心(1)”)。然后将这一过程再重复两次。在第三次迭代之后,为簇中心分配的数据点保持不变,因此算法结束。
给定新的数据点,k 均值会将其分配给最近的簇中心。下一个例子(图 3-24)展示了图 3-23 学到的簇中心的边界:
mglearn.plots.plot_kmeans_boundaries()
plt.tight_layout()
plt.savefig('Images/03Clustering-02.png', bbox_inches='tight')
plt.show()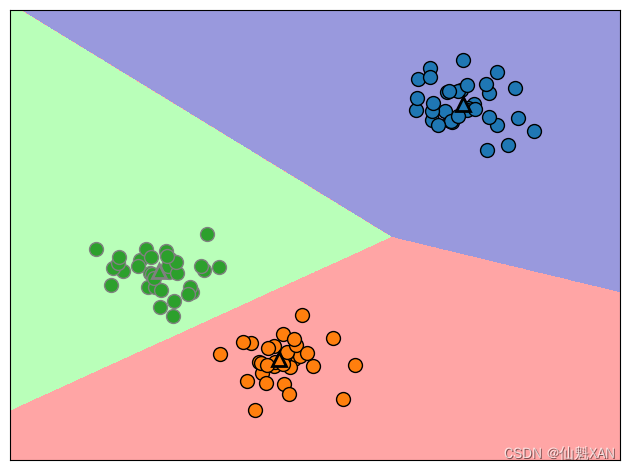
用 scikit-learn 应用 k 均值相当简单。下面我们将其应用于上图中的模拟数据。我们将 KMeans 类实例化,并设置我们要寻找的簇个数(如果不指定 n_clusters ,它的默认值是 8。使用这个值并没有什么特别的原因) 。然后对数据调用 fit 方法:
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# 生成模拟的二维数据
X, y = make_blobs(random_state=1)
# 构建聚类模型
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)算法运行期间,为 X 中的每个训练数据点分配一个簇标签。你可以在 kmeans.labels_ 属性中找到这些标签:
print("Cluster memberships:\n{}".format(kmeans.labels_))
因为我们要找的是 3 个簇,所以簇的编号是 0 到 2。
你也可以用 predict 方法为新数据点分配簇标签。预测时会将最近的簇中心分配给每个新数据点,但现有模型不会改变。对训练集运行 predict 会返回与 labels_ 相同的结果:
print(kmeans.predict(X))
可以看到,聚类算法与分类算法有些相似,每个元素都有一个标签。但并不存在真实的标签,因此标签本身并没有先验 意义。我们回到之前讨论过的人脸图像聚类的例子。聚类的结果可能是,算法找到的第 3 个簇仅包含你朋友 Bela 的面孔。但只有在查看图片之后才能知道这一点,而且数字 3 是任意的。算法给你的唯一信息就是所有标签为 3 的人脸都是相似的。
对于我们刚刚在二维玩具数据集上运行的聚类算法,这意味着我们不应该为其中一组的标签是 0、另一组的标签是 1 这一事实赋予任何意义。再次运行该算法可能会得到不同的簇编号,原因在于初始化的随机性质。
下面又给出了这个数据的图像(图 3-25)。簇中心被保存在 cluster_centers_ 属性中,我们用三角形表示它们:
mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, markers='o')
# 绘制簇中心
mglearn.discrete_scatter(
kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], [0, 1, 2],
markers='^', markeredgewidth=2)
# 显示图形
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.title("KMeans Clustering")
plt.tight_layout()
plt.savefig('Images/03Clustering-03.png', bbox_inches='tight')
plt.show()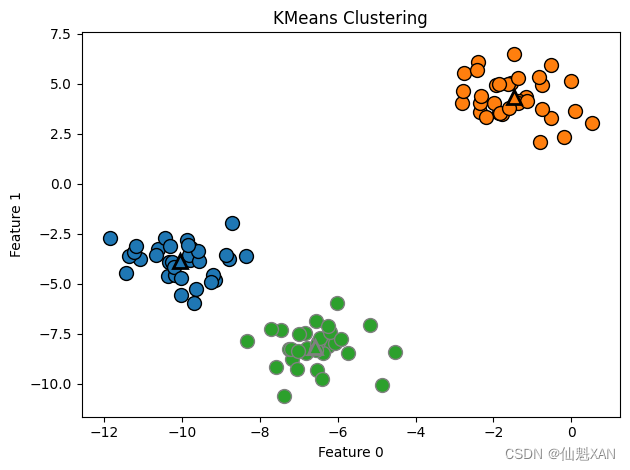
我们也可以使用更多或更少的簇中心(图 3-26):
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
# 使用2个簇中心:
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
assignments = kmeans.labels_
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignments, ax=axes[0])
# 使用5个簇中心:
kmeans = KMeans(n_clusters=5)
kmeans.fit(X)
assignments = kmeans.labels_
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignments, ax=axes[1])
plt.tight_layout()
plt.savefig('Images/03Clustering-03.png', bbox_inches='tight')
plt.show()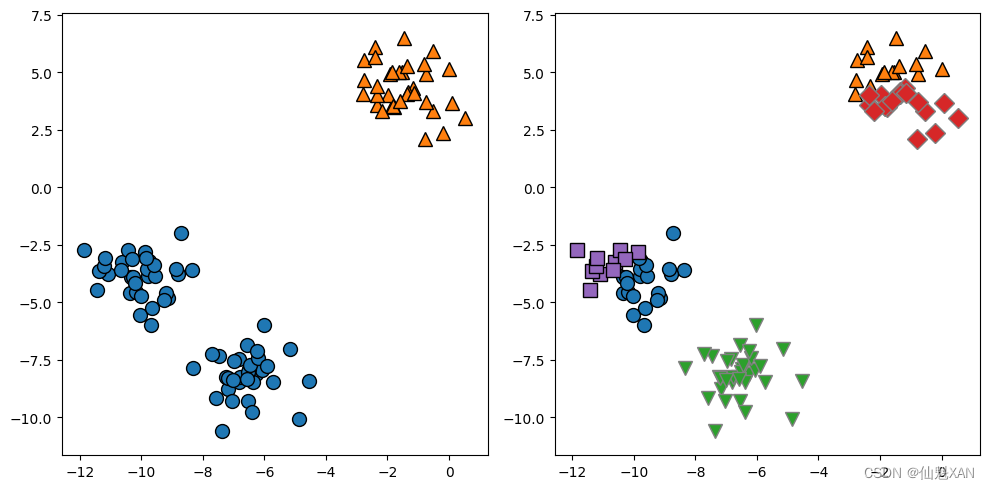
1)k 均值的失败案例
即使你知道给定数据集中簇的“正确”个数,k 均值可能也不是总能找到它们。每个簇仅由其中心定义,这意味着每个簇都是凸形(convex)。因此,k 均值只能找到相对简单的形状。k 均值还假设所有簇在某种程度上具有相同的“直径”,它总是将簇之间的边界刚好画在簇中心的中间位置。有时这会导致令人惊讶的结果,如图 3-27 所示:
X_varied, y_varied = make_blobs(n_samples=200,
cluster_std=[1.0, 2.5, 0.5],
random_state=170)
y_pred = KMeans(n_clusters=3, random_state=0).fit_predict(X_varied)
mglearn.discrete_scatter(X_varied[:, 0], X_varied[:, 1], y_pred)
plt.legend(["cluster 0", "cluster 1", "cluster 2"], loc='best')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.tight_layout()
plt.savefig('Images/03Clustering-04.png', bbox_inches='tight')
plt.show()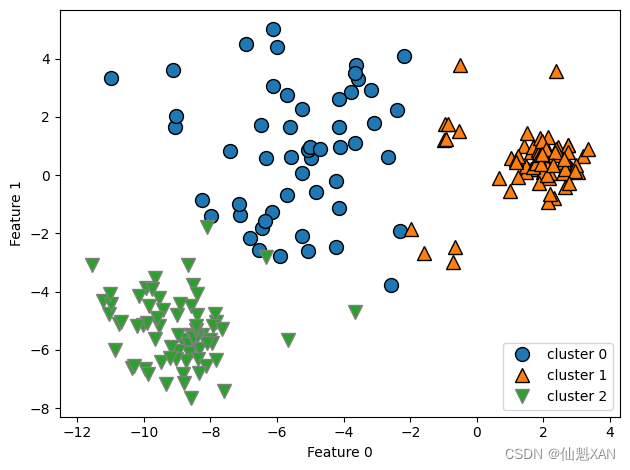
你可能会认为,左下方的密集区域是第一个簇,右上方的密集区域是第二个,中间密度较小的区域是第三个。但事实上,簇 0 和簇 1 都包含一些远离簇中其他点的点。
k 均值还假设所有方向对每个簇都同等重要。图 3-28 显示了一个二维数据集,数据中包含明确分开的三部分。但是这三部分被沿着对角线方向拉长。由于 k 均值仅考虑到最近簇中心的距离,所以它无法处理这种类型的数据:
# 生成一些随机分组数据
X, y = make_blobs(random_state=170, n_samples=600)
rng = np.random.RandomState(74)
# 变换数据使其拉长
# 生成一些随机分组数据
X, y = make_blobs(random_state=170, n_samples=600)
rng = np.random.RandomState(74)
# 变换数据使其拉长
transformation = rng.normal(size=(2, 2))
X = np.dot(X, transformation)
# 将数据聚类成3个簇
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
y_pred = kmeans.predict(X)
# 画出簇分配和簇中心
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap=mglearn.cm3)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
marker='^', c=[0, 1, 2], s=100, linewidth=2, cmap=mglearn.cm3)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.tight_layout()
plt.savefig('Images/03Clustering-05.png', bbox_inches='tight')
plt.show()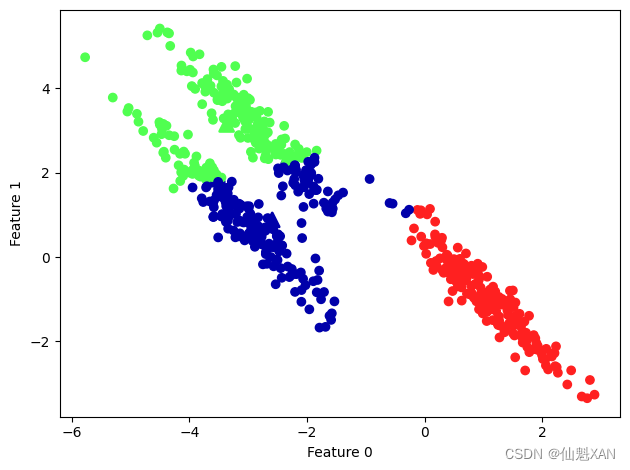
如果簇的形状更加复杂,比如我们在第 2 章遇到的 two_moons 数据,那么 k 均值的表现也很差(见图 3-29):
# 生成模拟的two_moons数据(这次的噪声较小)
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 将数据聚类成2个簇
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
y_pred = kmeans.predict(X)
# 画出簇分配和簇中心
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap=mglearn.cm2, s=60)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
marker='^', c=[mglearn.cm2(0), mglearn.cm2(1)], s=100, linewidth=2)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.tight_layout()
plt.savefig('Images/03Clustering-06.png', bbox_inches='tight')
plt.show()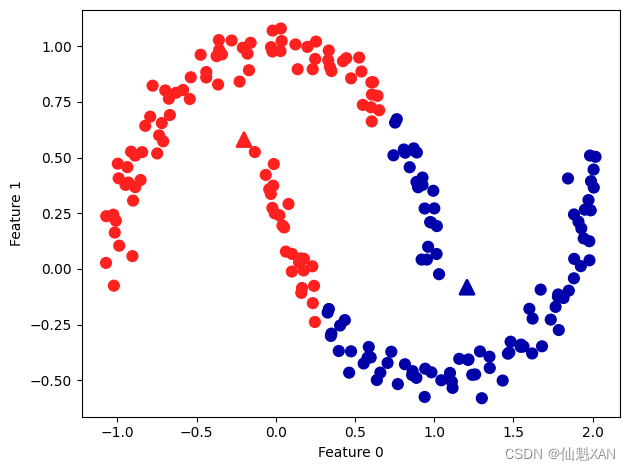
这里我们希望聚类算法能够发现两个半月形。但利用 k 均值算法是不可能做到这一点的。
2)矢量量化,或者将 k 均值看作分解
虽然 k 均值是一种聚类算法,但在 k 均值和分解方法(比如之前讨论过的 PCA 和 NMF)之间存在一些有趣的相似之处。你可能还记得,PCA 试图找到数据中方差最大的方向,而 NMF 试图找到累加的分量,这通常对应于数据的“极值”或“部分”(见图 3-13)。两种方法都试图将数据点表示为一些分量之和。与之相反,k 均值则尝试利用簇中心来表示每个数据点。你可以将其看作仅用一个分量来表示每个数据点,该分量由簇中心给出。
这种观点将 k 均值看作是一种分解方法,其中每个点用单一分量来表示,这种观点被称为矢量量化 (vector quantization)。
我们来并排比较 PCA、NMF 和 k 均值,分别显示提取的分量(图 3-30),以及利用 100 个分量对测试集中人脸的重建(图 3-31)。对于 k 均值,重建就是在训练集中找到的最近的簇中心:
from sklearn.model_selection import train_test_split
import os
import shutil
from sklearn.datasets import get_data_home
from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import NMF
from sklearn.decomposition import PCA
# 获取数据缓存目录
data_home = get_data_home()
# 删除缓存的LFW数据集
lfw_dir = os.path.join(data_home, 'lfw_home')
if os.path.exists(lfw_dir):
shutil.rmtree(lfw_dir)
# 重新下载数据集
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7, download_if_missing=True)
image_shape = people.images[0].shape
# 创建一个掩码,用于选择每个人的前50张照片
mask = np.zeros(people.target.shape, dtype=bool)
for target in np.unique(people.target):
mask[np.where(people.target == target)[0][:50]] = True
# 使用掩码过滤数据
X_people = people.data[mask]
y_people = people.target[mask]
# 将灰度值缩放到0到1之间,而不是在0到255之间,以获得更好的数据稳定性
X_people = X_people / 255.0
X_train, X_test, y_train, y_test = train_test_split(
X_people, y_people, stratify=y_people, random_state=0)
nmf = NMF(n_components=100, random_state=0)
nmf.fit(X_train)
pca = PCA(n_components=100, random_state=0)
pca.fit(X_train)
kmeans = KMeans(n_clusters=100, random_state=0)
kmeans.fit(X_train)
X_reconstructed_pca = pca.inverse_transform(pca.transform(X_test))
X_reconstructed_kmeans = kmeans.cluster_centers_[kmeans.predict(X_test)]
X_reconstructed_nmf = np.dot(nmf.transform(X_test), nmf.components_)fig, axes = plt.subplots(3, 5, figsize=(8, 8),
subplot_kw={'xticks': (), 'yticks': ()})
fig.suptitle("Extracted Components")
for ax, comp_kmeans, comp_pca, comp_nmf in zip(
axes.T, kmeans.cluster_centers_, pca.components_, nmf.components_):
ax[0].imshow(comp_kmeans.reshape(image_shape))
ax[1].imshow(comp_pca.reshape(image_shape), cmap='viridis')
ax[2].imshow(comp_nmf.reshape(image_shape))
axes[0, 0].set_ylabel("kmeans")
axes[1, 0].set_ylabel("pca")
axes[2, 0].set_ylabel("nmf")
plt.tight_layout()
plt.savefig('Images/03Clustering-07.png', bbox_inches='tight')
plt.show()
fig, axes = plt.subplots(4, 5, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(8, 8))
fig.suptitle("Reconstructions")
for ax, orig, rec_kmeans, rec_pca, rec_nmf in zip(
axes.T, X_test, X_reconstructed_kmeans, X_reconstructed_pca,
X_reconstructed_nmf):
ax[0].imshow(orig.reshape(image_shape))
ax[1].imshow(rec_kmeans.reshape(image_shape))
ax[2].imshow(rec_pca.reshape(image_shape))
ax[3].imshow(rec_nmf.reshape(image_shape))
axes[0, 0].set_ylabel("original")
axes[1, 0].set_ylabel("kmeans")
axes[2, 0].set_ylabel("pca")
axes[3, 0].set_ylabel("nmf")
plt.tight_layout()
plt.savefig('Images/03Clustering-08.png', bbox_inches='tight')
plt.show()

利用 k 均值做矢量量化的一个有趣之处在于,可以用比输入维度更多的簇来对数据进行编码。让我们回到 two_moons 数据。利用 PCA 或 NMF,我们对这个数据无能为力,因为它只有两个维度。使用 PCA 或 NMF 将其降到一维,将会完全破坏数据的结构。但通过使用更多的簇中心,我们可以用 k 均值找到一种更具表现力的表示(见图 3-32):
# 生成模拟的two_moons数据(这次的噪声较小)
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
kmeans = KMeans(n_clusters=10, random_state=0)
kmeans.fit(X)
y_pred = kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=60, cmap='Paired')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=60,
marker='^', c=range(kmeans.n_clusters), linewidth=2, cmap='Paired')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
print("Cluster memberships:\n{}".format(y_pred))
plt.tight_layout()
plt.savefig('Images/03Clustering-09.png', bbox_inches='tight')
plt.show()Cluster memberships: [8 4 6 3 1 1 5 2 8 4 9 2 1 4 7 5 0 2 0 7 1 2 0 4 9 6 1 1 6 0 8 9 2 6 8 1 2 5 3 6 2 7 8 6 4 9 5 7 6 2 7 2 1 3 4 8 0 4 0 9 2 3 1 8 4 3 9 4 9 3 2 3 2 6 2 3 6 8 0 2 1 9 2 1 6 9 5 9 2 1 0 5 1 7 1 1 4 2 3 6 4 1 9 5 3 6 3 7 4 0 7 9 9 3 8 4 8 1 2 8 8 7 6 9 6 7 5 6 4 1 5 7 3 6 4 4 4 3 1 8 6 6 0 9 7 5 6 4 0 6 2 4 8 0 2 9 4 2 0 0 6 4 0 4 2 1 0 2 4 2 0 3 3 7 6 2 1 7 7 0 4 3 1 4 1 0 9 2 3 7 3 0 8 5 6 7 1 6 9 4]
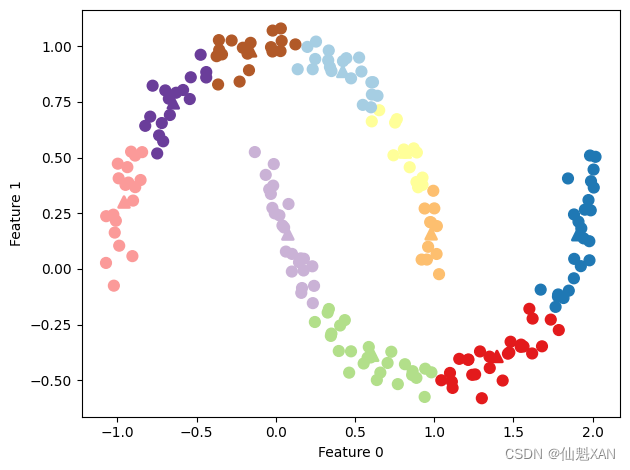
我们使用了 10 个簇中心,也就是说,现在每个点都被分配了 0 到 9 之间的一个数字。我们可以将其看作 10 个分量表示的数据(我们有 10 个新特征),只有表示该点对应的簇中心的那个特征不为 0,其他特征均为 0。利用这个 10 维表示,现在可以用线性模型来划分两个半月形,而利用原始的两个特征是不可能做到这一点的。将到每个簇中心的距离作为特征,还可以得到一种表现力更强的数据表示。可以利用 kmeans 的 transform 方法来完成这一点:
distance_features = kmeans.transform(X)
print("Distance feature shape: {}".format(distance_features.shape))
print("Distance features:\n{}".format(distance_features))Distance feature shape: (200, 10) Distance features: [[0.53664613 1.15017588 0.93237626 ... 1.48034956 0.002907 1.07736639] [1.74138152 0.60592307 1.00666225 ... 2.52921971 1.20779969 2.23716489] [0.75710543 1.93145038 0.91586549 ... 0.78321505 0.87573753 0.71838465] ... [0.9274342 1.73811046 0.57899268 ... 1.11471941 0.83358544 1.04125672] [0.3227627 1.97647071 1.47861069 ... 0.81425026 0.84551232 0.28446737] [1.63322944 0.47226506 1.02289983 ... 2.46626118 1.09767675 2.14812753]]
k 均值是非常流行的聚类算法,因为它不仅相对容易理解和实现,而且运行速度也相对较快。k 均值可以轻松扩展到大型数据集,scikit-learn 甚至在 MiniBatchKMeans 类中包含了一种更具可扩展性的变体,可以处理非常大的数据集。
k 均值的缺点之一在于,它依赖于随机初始化,也就是说,算法的输出依赖于随机种子。默认情况下,scikit-learn 用 10 种不同的随机初始化将算法运行 10 次,并返回最佳结果(在这种情况下,“最佳”的意思是簇的方差之和最小)。k 均值还有一个缺点,就是对簇形状的假设的约束性较强,而且还要求指定所要寻找的簇的个数(在现实世界的应用中可能并不知道这个数字)。
接下来,我们将学习另外两种聚类算法,它们都在某些方面对这些性质做了改进。
2、凝聚聚类(agglomerative clustering)
凝聚聚类 (agglomerative clustering)指的是许多基于相同原则构建的聚类算法,这一原则是:算法首先声明每个点是自己的簇,然后合并两个最相似的簇,直到满足某种停止准则为止。scikit-learn 中实现的停止准则是簇的个
数,因此相似的簇被合并,直到仅剩下指定个数的簇。还有一些链接 (linkage)准则,规定如何度量“最相似的簇”。这种度量总是定义在两个现有的簇之间。
scikit-learn中实现了以下三种选项
ward默认选项。
ward挑选两个簇来合并,使得所有簇中的方差增加最小。这通常会得到大小差不多相等的簇。
average
average链接将簇中所有点之间平均距离最小的两个簇合并。
complete
complete链接(也称为最大链接)将簇中点之间最大距离最小的两个簇合并。
ward 适用于大多数数据集,在我们的例子中将使用它。如果簇中的成员个数非常不同(比如其中一个比其他所有都大得多),那么 average 或 complete 可能效果更好。
图 3-33 给出了在一个二维数据集上的凝聚聚类过程,要寻找三个簇。
mglearn.plots.plot_agglomerative_algorithm()
plt.tight_layout()
plt.savefig('Images/03Clustering-10.png', bbox_inches='tight')
plt.show()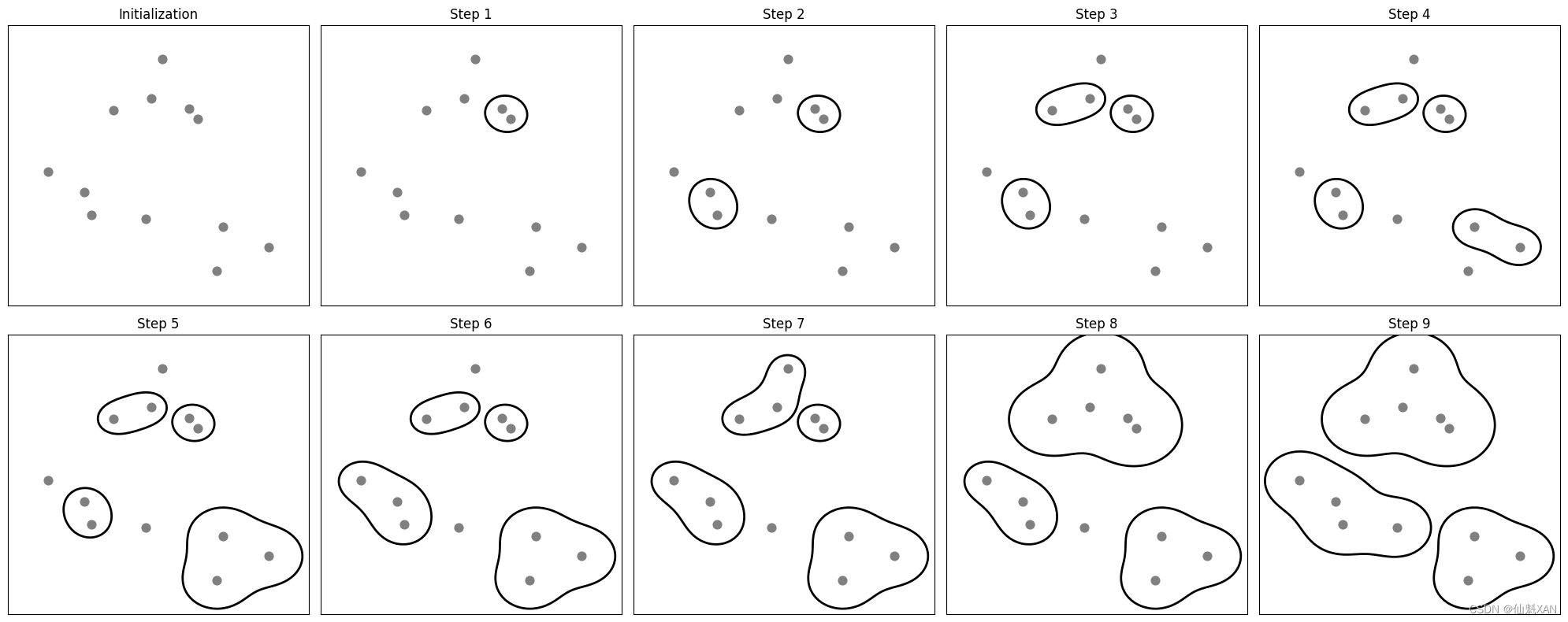
最开始,每个点自成一簇。然后在每一个步骤中,相距最近的两个簇被合并。在前四个步骤中,选出两个单点簇并将其合并成两点簇。在步骤 5(Step 5)中,其中一个两点簇被扩展到三个点,以此类推。在步骤 9(Step 9)中,只剩下 3 个簇。由于我们指定寻找 3 个簇,因此算法结束。
我们来看一下凝聚聚类对我们这里使用的简单三簇数据的效果如何。由于算法的工作原理,凝聚算法不能对新数据点做出预测。因此 AgglomerativeClustering 没有 predict 方法。为了构造模型并得到训练集上簇的成员关系,可以改用 fit_predict 方法(我们也可以使用 labels_ 属性,正如 k 均值所做的那样)。结果如图 3-34 所示。
from sklearn.datasets import make_blobs
from sklearn.cluster import AgglomerativeClustering
X, y = make_blobs(random_state=1)
agg = AgglomerativeClustering(n_clusters=3)
assignment = agg.fit_predict(X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignment)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.tight_layout()
plt.savefig('Images/03Clustering-11.png', bbox_inches='tight')
plt.show()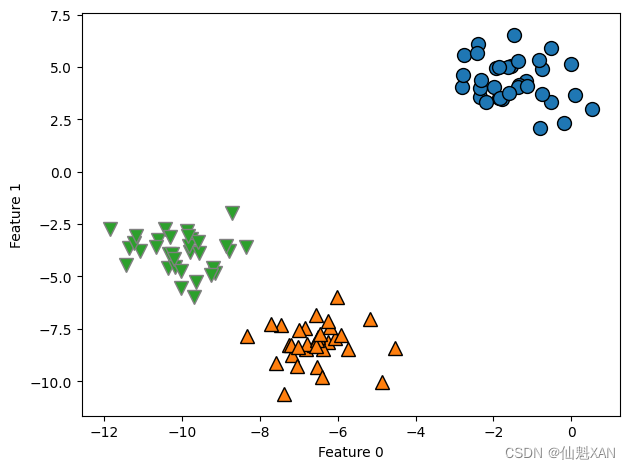
正如所料,算法完美地完成了聚类。虽然凝聚聚类的 scikit-learn 实现需要你指定希望算法找到的簇的个数,但凝聚聚类方法为选择正确的个数提供了一些帮助,我们将在下面讨论。
1)层次聚类与树状图
凝聚聚类生成了所谓的层次聚类 (hierarchical clustering)。聚类过程迭代进行,每个点都从一个单点簇变为属于最终的某个簇。每个中间步骤都提供了数据的一种聚类(簇的个数也不相同)。有时候,同时查看所有可能的聚类是有帮助的。下一个例子(图 3-35)叠加显示了图 3-33 中所有可能的聚类,有助于深入了解每个簇如何分解为较小的簇:
mglearn.plots.plot_agglomerative()
plt.tight_layout()
plt.savefig('Images/03Clustering-12.png', bbox_inches='tight')
plt.show()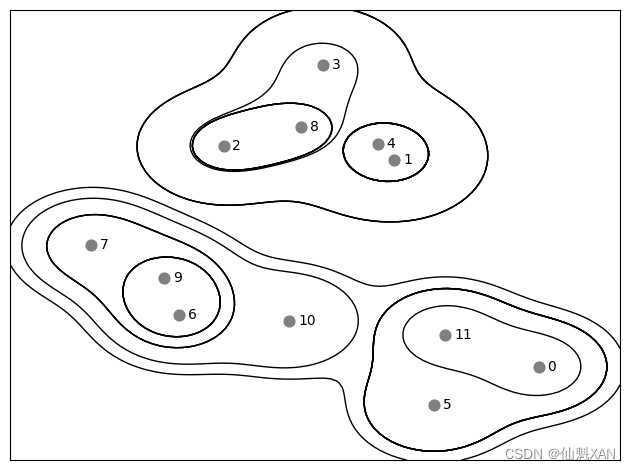
虽然这种可视化为层次聚类提供了非常详细的视图,但它依赖于数据的二维性质,因此不能用于具有两个以上特征的数据集。但还有另一个将层次聚类可视化的工具,叫作树状图 (dendrogram),它可以处理多维数据集。
不幸的是,目前 scikit-learn 没有绘制树状图的功能。但你可以利用 SciPy 轻松生成树状图。SciPy 的聚类算法接口与 scikit-learn 的聚类算法稍有不同。SciPy 提供了一个函数,接受数据数组 X 并计算出一个链接数组 (linkage array),它对层次聚类的相似度进行编码。然后我们可以将这个链接数组提供给 scipy 的 dendrogram 函数来绘制树状图(图 3-36)。
# 从SciPy中导入dendrogram函数和ward聚类函数
from scipy.cluster.hierarchy import dendrogram, ward
X, y = make_blobs(random_state=0, n_samples=12)
# 将ward聚类应用于数据数组X
# SciPy的ward函数返回一个数组,指定执行凝聚聚类时跨越的距离
linkage_array = ward(X)
# 现在为包含簇之间距离的linkage_array绘制树状图
dendrogram(linkage_array)
# 在树中标记划分成两个簇或三个簇的位置
ax = plt.gca()
bounds = ax.get_xbound()
ax.plot(bounds, [7.25, 7.25], '--', c='k')
ax.plot(bounds, [4, 4], '--', c='k')
ax.text(bounds[1], 7.25, ' two clusters', va='center', fontdict={'size': 15})
ax.text(bounds[1], 4, ' three clusters', va='center', fontdict={'size': 15})
plt.xlabel("Sample index")
plt.ylabel("Cluster distance")
plt.tight_layout()
plt.savefig('Images/03Clustering-13.png', bbox_inches='tight')
plt.show()
树状图在底部显示数据点(编号从 0 到 11)。然后以这些点(表示单点簇)作为叶节点绘制一棵树,每合并两个簇就添加一个新的父节点。
从下往上看,数据点 1 和 4 首先被合并(正如你在图 3-33 中所见)。接下来,点 6 和 9 被合并为一个簇,以此类推。在顶层有两个分支,一个由点 11、0、5、10、7、6 和 9 组成,另一个由点 1、4、3、2 和 8 组成。这对应于图中左侧两个最大的簇。
树状图的 y 轴不仅说明凝聚算法中两个簇何时合并,每个分支的长度还表示被合并的簇之间的距离。在这张树状图中,最长的分支是用标记为“three clusters”(三个簇)的虚线表示的三条线。它们是最长的分支,这表示从三个簇到两个簇的过程中合并了一些距离非常远的点。我们在图像上方再次看到这一点,将剩下的两个簇合并为一个簇也需要跨越相对较大的距离。
不幸的是,凝聚聚类仍然无法分离像 two_moons 数据集这样复杂的形状。但我们要学习的下一个算法 DBSCAN 可以解决这个问题。
3、DBSCAN
另一个非常有用的聚类算法是 DBSCAN(density-based spatial clustering of applications with noise,即“具有噪声的基于密度的空间聚类应用”)。DBSCAN 的主要优点是它不需要用户先验 地设置簇的个数,可以划分具有复杂形状的簇,还可以找出不属于任何簇的点。DBSCAN 比凝聚聚类和 k 均值稍慢,但仍可以扩展到相对较大的数据集。
DBSCAN 的原理是识别特征空间的“拥挤”区域中的点,在这些区域中许多数据点靠近在一起。这些区域被称为特征空间中的密集 (dense)区域。DBSCAN 背后的思想是,簇形成数据的密集区域,并由相对较空的区域分隔开。
在密集区域内的点被称为核心样本 (core sample,或核心点),它们的定义如下。DBSCAN 有两个参数:min_samples 和 eps 。如果在距一个给定数据点 eps 的距离内至少有 min_samples 个数据点,那么这个数据点就是核心样本。DBSCAN 将彼此距离小于 eps 的核心样本放到同一个簇中。
算法首先任意选取一个点,然后找到到这个点的距离小于等于 eps 的所有的点。如果距起始点的距离在 eps 之内的数据点个数小于 min_samples ,那么这个点被标记为噪声 (noise),也就是说它不属于任何簇。如果距离在 eps 之内的数据点个数大于 min_samples ,则这个点被标记为核心样本,并被分配一个新的簇标签。然后访问该点的所有邻居(在距离 eps 以内)。如果它们还没有被分配一个簇,那么就将刚刚创建的新的簇标签分配给它们。如果它们是核心样本,那么就依次访问其邻居,以此类推。簇逐渐增大,直到在簇的 eps 距离内没有更多的核心样本为止。然后选取另一个尚未被访问过的点,并重复相同的过程。
最后,一共有三种类型的点:核心点、与核心点的距离在 eps 之内的点(叫作边界点 ,boundary point)和噪声。如果 DBSCAN 算法在特定数据集上多次运行,那么核心点的聚类始终相同,同样的点也始终被标记为噪声。但边界点可能与不止一个簇的核心样本相邻。因此,边界点所属的簇依赖于数据点的访问顺序。一般来说只有很少的边界点,这种对访问顺序的轻度依赖并不重要。
我们将 DBSCAN 应用于演示凝聚聚类的模拟数据集。与凝聚聚类类似,DBSCAN 也不允许对新的测试数据进行预测,所以我们将使用 fit_predict 方法来执行聚类并返回簇标签。
from sklearn.cluster import DBSCAN
X, y = make_blobs(random_state=0, n_samples=12)
dbscan = DBSCAN()
clusters = dbscan.fit_predict(X)
print("Cluster memberships:\n{}".format(clusters))Cluster memberships: [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
如你所见,所有数据点都被分配了标签 -1 ,这代表噪声。这是 eps 和 min_samples 默认参数设置的结果,对于小型的玩具数据集并没有调节这些参数。min_samples 和 eps 取不同值时的簇分类如下所示,其可视化结果见图 3-37。
mglearn.plots.plot_dbscan()
plt.tight_layout()
plt.savefig('Images/03Clustering-14.png', bbox_inches='tight')
plt.show()min_samples: 2 eps: 1.000000 cluster: [-1 0 0 -1 0 -1 1 1 0 1 -1 -1] min_samples: 2 eps: 1.500000 cluster: [0 1 1 1 1 0 2 2 1 2 2 0] min_samples: 2 eps: 2.000000 cluster: [0 1 1 1 1 0 0 0 1 0 0 0] min_samples: 2 eps: 3.000000 cluster: [0 0 0 0 0 0 0 0 0 0 0 0] min_samples: 3 eps: 1.000000 cluster: [-1 0 0 -1 0 -1 1 1 0 1 -1 -1] min_samples: 3 eps: 1.500000 cluster: [0 1 1 1 1 0 2 2 1 2 2 0] min_samples: 3 eps: 2.000000 cluster: [0 1 1 1 1 0 0 0 1 0 0 0] min_samples: 3 eps: 3.000000 cluster: [0 0 0 0 0 0 0 0 0 0 0 0] min_samples: 5 eps: 1.000000 cluster: [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1] min_samples: 5 eps: 1.500000 cluster: [-1 0 0 0 0 -1 -1 -1 0 -1 -1 -1] min_samples: 5 eps: 2.000000 cluster: [-1 0 0 0 0 -1 -1 -1 0 -1 -1 -1] min_samples: 5 eps: 3.000000 cluster: [0 0 0 0 0 0 0 0 0 0 0 0]

在这张图中,属于簇的点是实心的,而噪声点则显示为空心的。核心样本显示为较大的标记,而边界点则显示为较小的标记。增大 eps (在图中从左到右),更多的点会被包含在一个簇中。这让簇变大,但可能也会导致多个簇合并成一个。增大 min_samples (在图中从上到下),核心点会变得更少,更多的点被标记为噪声。
参数 eps 在某种程度上更加重要,因为它决定了点与点之间“接近”的含义。将 eps 设置得非常小,意味着没有点是核心样本,可能会导致所有点都被标记为噪声。将 eps 设置得非常大,可能会导致所有点形成单个簇。
设置 min_samples 主要是为了判断稀疏区域内的点被标记为异常值还是形成自己的簇。如果增大 min_samples ,任何一个包含少于 min_samples 个样本的簇现在将被标记为噪声。因此,min_samples 决定簇的最小尺寸。在图 3-37 中 eps=1.5 时,从 min_samples=3 到 min_samples=5 ,你可以清楚地看到这一点。min_samples=3 时有三个簇:一个包含 4 个点,一个包含 5 个点,一个包含 3 个点。min_samples=5 时,两个较小的簇(分别包含 3 个点和 4 个点)现在被标记为噪声,只保留包含 5 个样本的簇。
虽然 DBSCAN 不需要显式地设置簇的个数,但设置 eps 可以隐式地控制找到的簇的个数。使用 StandardScaler 或 MinMaxScaler 对数据进行缩放之后,有时会更容易找到 eps 的较好取值,因为使用这些缩放技术将确保所有特征具有相似的范围。
图 3-38 展示了在 two_moons 数据集上运行 DBSCAN 的结果。利用默认设置,算法找到了两个半圆形并将其分开:
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 将数据缩放成平均值为0、方差为1
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
dbscan = DBSCAN()
clusters = dbscan.fit_predict(X_scaled)
# 绘制簇分配
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm2, s=60)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.tight_layout()
plt.savefig('Images/03Clustering-15.png', bbox_inches='tight')
plt.show()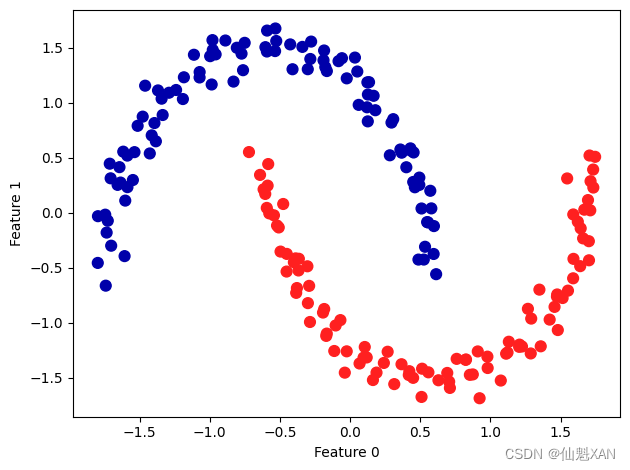
由于算法找到了我们想要的簇的个数(2 个),因此参数设置的效果似乎很好。如果将 eps 减小到 0.2 (默认值为 0.5 ),我们将会得到 8 个簇,这显然太多了。将 eps 增大到 0.7 则会导致只有一个簇。
在使用 DBSCAN 时,你需要谨慎处理返回的簇分配。如果使用簇标签对另一个数据进行索引,那么使用 -1 表示噪声可能会产生意料之外的结果。
4、聚类算法的对比与评估
在应用聚类算法时,其挑战之一就是很难评估一个算法的效果好坏,也很难比较不同算法的结果。在讨论完 k 均值、凝聚聚类和 DBSCAN 背后的算法之后,下面我们将在一些现实世界的数据集上比较它们。
1)用真实值评估聚类
有一些指标可用于评估聚类算法相对于真实聚类的结果,其中最重要的是调整 rand 指数 (adjusted rand index,ARI)和归一化互信息 (normalized mutual information,NMI),二者都给出了定量的度量,其最佳值为 1,0 表示不相关的聚类(虽然 ARI 可以取负值)。
下面我们使用 ARI 来比较 k 均值、凝聚聚类和 DBSCAN 算法。为了对比,我们还添加了将点随机分配到两个簇中的图像(见图 3-39)。
from sklearn.metrics.cluster import adjusted_rand_score
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 将数据缩放成平均值为0、方差为1
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
fig, axes = plt.subplots(1, 4, figsize=(15, 3),
subplot_kw={'xticks': (), 'yticks': ()})
# 列出要使用的算法
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2),
DBSCAN()]
# 创建一个随机的簇分配,作为参考
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(X))
# 绘制随机分配
axes[0].scatter(X_scaled[:, 0], X_scaled[:, 1], c=random_clusters,
cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment - ARI: {:.2f}".format(
adjusted_rand_score(y, random_clusters)))
for ax, algorithm in zip(axes[1:], algorithms):
# 绘制簇分配和簇中心
clusters = algorithm.fit_predict(X_scaled)
ax.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters,
cmap=mglearn.cm3, s=60)
ax.set_title("{} - ARI: {:.2f}".format(algorithm.__class__.__name__,
adjusted_rand_score(y, clusters)))
plt.tight_layout()
plt.savefig('Images/03Clustering-16.png', bbox_inches='tight')
plt.show()

调整 rand 指数给出了符合直觉的结果,随机簇分配的分数为 0,而 DBSCAN(完美地找到了期望中的聚类)的分数为 1。
用这种方式评估聚类时,一个常见的错误是使用 accuracy_score 而不是 adjusted_rand_score 、normalized_mutual_info_score 或其他聚类指标。使用精度的问题在于,它要求分配的簇标签与真实值完全匹配。但簇标签本身毫无意义——唯一重要的是哪些点位于同一个簇中。
from sklearn.metrics import accuracy_score
# 这两种点标签对应于相同的聚类
clusters1 = [0, 0, 1, 1, 0]
clusters2 = [1, 1, 0, 0, 1]
# 精度为0,因为二者标签完全不同
print("Accuracy: {:.2f}".format(accuracy_score(clusters1, clusters2)))
# 调整rand分数为1,因为二者聚类完全相同
print("ARI: {:.2f}".format(adjusted_rand_score(clusters1, clusters2)))Accuracy: 0.00 ARI: 1.00
2)在没有真实值的情况下评估聚类
我们刚刚展示了一种评估聚类算法的方法,但在实践中,使用诸如 ARI 之类的指标有一个很大的问题。在应用聚类算法时,通常没有真实值来比较结果。如果我们知道了数据的正确聚类,那么可以使用这一信息构建一个监督模型(比如分类器)。因此,使用类似 ARI 和 NMI 的指标通常仅有助于开发算法,但对评估应用是否成功没有帮助。
有一些聚类的评分指标不需要真实值,比如轮廓系数 (silhouette coeffcient)。但它们在实践中的效果并不好。轮廓分数计算一个簇的紧致度,其值越大越好,最高分数为 1。虽然紧致的簇很好,但紧致度不允许复杂的形状。
下面是一个例子,利用轮廓分数在 two_moons 数据集上比较 k 均值、凝聚聚类和 DBSCAN(图 3-40):
from sklearn.metrics.cluster import silhouette_score
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 将数据缩放成平均值为0、方差为1
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
fig, axes = plt.subplots(1, 4, figsize=(15, 3),
subplot_kw={'xticks': (), 'yticks': ()})
# 创建一个随机的簇分配,作为参考
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(X))
# 绘制随机分配
axes[0].scatter(X_scaled[:, 0], X_scaled[:, 1], c=random_clusters,
cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment: {:.2f}".format(
silhouette_score(X_scaled, random_clusters)))
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2),
DBSCAN()]
for ax, algorithm in zip(axes[1:], algorithms):
clusters = algorithm.fit_predict(X_scaled)
# 绘制簇分配和簇中心
ax.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm3,
s=60)
ax.set_title("{} : {:.2f}".format(algorithm.__class__.__name__,
silhouette_score(X_scaled, clusters)))
plt.tight_layout()
plt.savefig('Images/03Clustering-17.png', bbox_inches='tight')
plt.show()
如你所见,k 均值的轮廓分数最高,尽管我们可能更喜欢 DBSCAN 的结果。对于评估聚类,稍好的策略是使用基于鲁棒性的 (robustness-based)聚类指标。这种指标先向数据中添加一些噪声,或者使用不同的参数设定,然后运行算法,并对结果进行比较。其思想是,如果许多算法参数和许多数据扰动返回相同的结果,那么它很可能是可信的。不幸的是,在写作本书时,scikit-learn 还没有实现这一策略。
即使我们得到一个鲁棒性很好的聚类或者非常高的轮廓分数,但仍然不知道聚类中是否有任何语义含义,或者聚类是否反映了数据中我们感兴趣的某个方面。我们回到人脸图像的例子。我们希望找到类似人脸的分组,比如男人和女人、老人和年轻人,或者有胡子的人和没胡子的人。假设我们将数据分为两个簇,关于哪些点应该被聚类在一起,所有算法的结果一致。我们仍不知道找到的簇是否以某种方式对应于我们感兴趣的概念。算法找到的可能是侧视图和正面视图、夜间拍摄的照片和白天拍摄的照片,或者 iPhone 拍摄的照片和安卓手机拍摄的照片。要想知道聚类是否对应于我们感兴趣的内容,唯一的办法就是对簇进行人工分析。
3)在人脸数据集上比较算法
我们将 k 均值、DBSCAN 和凝聚聚类算法应用于 Wild 数据集中的 Labeled Faces,并查看它们是否找到了有趣的结构。我们将使用数据的特征脸表示,它由包含 100 个成分的 PCA(whiten=True) 生成:
# 从lfw数据中提取特征脸,并对数据进行变换
from sklearn.decomposition import PCA
pca = PCA(n_components=100, whiten=True, random_state=0)
pca.fit_transform(X_people)
X_pca = pca.transform(X_people)我们之前见到,与原始像素相比,这是对人脸图像的一种语义更强的表示。它的计算速度也更快。这里有一个很好的练习,就是在原始数据上运行下列实验,不要用 PCA,并观察你是否能找到类似的簇。
用 DBSCAN 分析人脸数据集 。我们首先应用刚刚讨论过的 DBSCAN:
# 应用默认参数的DBSCAN
dbscan = DBSCAN()
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))Unique labels: [-1]
我们看到,所有返回的标签都是 -1,因此所有数据都被 DBSCAN 标记为“噪声”。我们可以改变两个参数来改进这一点:第一,我们可以增大 eps ,从而扩展每个点的邻域;第二,我们可以减小 min_samples ,从而将更小的点组视为簇。我们首先尝试改变 min_samples :
dbscan = DBSCAN(min_samples=3)
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))Unique labels: [-1]
即使仅考虑由三个点构成的组,所有点也都被标记为噪声。因此我们需要增大 eps :
dbscan = DBSCAN(min_samples=3, eps=15)
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))Unique labels: [-1 0]
使用更大的 eps (其值为 15 ),我们只得到了单一簇和噪声点。我们可以利用这一结果找出“噪声”相对于其他数据的形状。为了进一步理解发生的事情,我们查看有多少点是噪声,有多少点在簇内:
# 计算所有簇中的点数和噪声中的点数。
# bincount不允许负值,所以我们需要加1。
# 结果中的第一个数字对应于噪声点。
print("Number of points per cluster: {}".format(np.bincount(labels + 1)))Number of points per cluster: [ 37 2026]
噪声点非常少——只有 37 个,因此我们可以查看所有的噪声点(见图 3-41):
noise = X_people[labels==-1]
fig, axes = plt.subplots(3, 9, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(12, 4))
for image, ax in zip(noise, axes.ravel()):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
plt.tight_layout()
plt.savefig('Images/03Clustering-18.png', bbox_inches='tight')
plt.show()
没有显示,可以参看下面效果

将这些图像与图 3-7 中随机选择的人脸图像样本进行比较,我们可以猜测它们被标记为噪声的原因:第 1 行第 5 张图像显示一个人正在用玻璃杯喝水,还有人戴帽子的图像,在最后一张图像中,人脸前面有一只手。其他图像都包含奇怪的角度,或者太近或太宽的剪切。
这种类型的分析——尝试找出“奇怪的那一个”——被称为异常值检测 (outlier detection)。如果这是一个真实的应用,那么我们可能会尝试更好地裁切图像,以得到更加均匀的数据。对于照片中的人有时戴着帽子、喝水或在面前举着某物,我们能做的事情很少。但需要知道它们是数据中存在的问题,我们应用任何算法都需要解决这些问题。
如果我们想要找到更有趣的簇,而不是一个非常大的簇,那么需要将 eps 设置得更小,取值在 15 和 0.5 (默认值)之间。我们来看一下 eps 不同取值对应的结果:
for eps in [1, 3, 5, 7, 9, 11, 13]:
print("\neps={}".format(eps))
dbscan = DBSCAN(eps=eps, min_samples=3)
labels = dbscan.fit_predict(X_pca)
print("Clusters present: {}".format(np.unique(labels)))
print("Cluster sizes: {}".format(np.bincount(labels + 1)))eps=1 Clusters present: [-1] Cluster sizes: [2063] eps=3 Clusters present: [-1] Cluster sizes: [2063] eps=5 Clusters present: [-1 0] Cluster sizes: [2059 4] eps=7 Clusters present: [-1 0 1 2 3 4 5 6] Cluster sizes: [1954 75 4 14 6 4 3 3] eps=9 Clusters present: [-1 0 1] Cluster sizes: [1199 861 3] eps=11 Clusters present: [-1 0] Cluster sizes: [ 403 1660] eps=13 Clusters present: [-1 0] Cluster sizes: [ 119 1944]
对于较小的 eps ,所有点都被标记为噪声。eps=7 时,我们得到许多噪声点和许多较小的簇。eps=9 时,我们仍得到许多噪声点,但我们得到了一个较大的簇和一些较小的簇。从 eps=11 开始,我们仅得到一个较大的簇和噪声。
有趣的是,较大的簇从来没有超过一个。最多有一个较大的簇包含大多数点,还有一些较小的簇。这表示数据中没有两类或三类非常不同的人脸图像,而是所有图像或多或少地都与其他图像具有相同的相似度(或不相似度)。
eps=7 的结果看起来最有趣,它有许多较小的簇。我们可以通过将 13 个较小的簇中的点全部可视化来深入研究这一聚类(图 3-42):
dbscan = DBSCAN(min_samples=3, eps=7)
labels = dbscan.fit_predict(X_pca)
for cluster in range(max(labels) + 1):
mask = labels == cluster
n_images = np.sum(mask)
fig, axes = plt.subplots(1, n_images, figsize=(n_images * 1.5, 4),
subplot_kw={'xticks': (), 'yticks': ()})
for image, label, ax in zip(X_people[mask], y_people[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title(people.target_names[label].split()[-1])

有一些簇对应于(这个数据集中)脸部非常不同的人,比如 Sharon(沙龙)或 Koizumi(小泉)。在每个簇内,人脸方向和面部表情也是固定的。有些簇中包含多个人的面孔,但他们的方向和表情都相似。
这就是我们将 DBSCAN 算法应用于人脸数据集的分析结论。如你所见,我们这里进行了人工分析,不同于监督学习中基于 R2 分数或精度的更为自动化的搜索方法。
下面我们将继续应用 k 均值和凝聚聚类。
用 k 均值分析人脸数据集 。我们看到,利用 DBSCAN 无法创建多于一个较大的簇。凝聚聚类和 k 均值更可能创建均匀大小的簇,但我们需要设置簇的目标个数。我们可以将簇的数量设置为数据集中的已知人数,虽然无监督聚类算法不太可能完全找到它们。相反,我们可以首先设置一个比较小的簇的数量,比如 10 个,这样我们可以分析每个簇:
# 用k均值提取簇
km = KMeans(n_clusters=10, random_state=0)
labels_km = km.fit_predict(X_pca)
print("Cluster sizes k-means: {}".format(np.bincount(labels_km)))Cluster sizes k-means: [ 5 286 190 275 185 493 1 286 2 340]
如你所见,k 均值聚类将数据划分为大小相似的簇,其大小在 64 和 386 之间。这与 DBSCAN 的结果非常不同。
我们可以通过将簇中心可视化来进一步分析 k 均值的结果(图 3-43)。由于我们是在 PCA 生成的表示中进行聚类,因此我们需要使用 pca.inverse_transform 将簇中心旋转回到原始空间并可视化:
fig, axes = plt.subplots(2, 5, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(12, 4))
for center, ax in zip(km.cluster_centers_, axes.ravel()):
ax.imshow(pca.inverse_transform(center).reshape(image_shape),
vmin=0, vmax=1)
k 均值找到的簇中心是非常平滑的人脸。这并不奇怪,因为每个簇中心都是 64 到 386 张人脸图像的平均。使用降维的 PCA 表示,可以增加图像的平滑度(对比图 3-11 中利用 100 个 PCA 维度重建的人脸)。聚类似乎捕捉到人脸的不同方向、不同表情(第 3 个簇中心似乎显示的是一张笑脸),以及是否有衬衫领子(见倒数第二个簇中心)。
图 3-44 给出了更详细的视图,我们对每个簇中心给出了簇中 5 张最典型的图像(该簇中与簇中心距离最近的图像)与 5 张最不典型的图像(该簇中与簇中心距离最远的图像):
mglearn.plots.plot_kmeans_faces(km, pca, X_pca, X_people,
y_people, people.target_names)
图 3-44 证实了我们认为第 3 个簇是笑脸的直觉,也证实了其他簇中方向的重要性。不过“非典型的”点与簇中心不太相似,而且它们的分配似乎有些随意。这可以归因于以下事实:k 均值对所有数据点进行划分,不像 DBSCAN 那样具有“噪声”点的概念。利用更多数量的簇,算法可以找到更细微的区别。但添加更多的簇会使得人工检查更加困难。
用凝聚聚类分析人脸数据集 。下面我们来看一下凝聚聚类的结果:
# 用ward凝聚聚类提取簇
agglomerative = AgglomerativeClustering(n_clusters=10)
labels_agg = agglomerative.fit_predict(X_pca)
print("Cluster sizes agglomerative clustering: {}".format(
np.bincount(labels_agg)))Cluster sizes agglomerative clustering: [264 100 275 553 49 64 546 52 51 109]
凝聚聚类生成的也是大小相近的簇,其大小在 26 和 623 之间。这比 k 均值生成的簇更不均匀,但比 DBSCAN 生成的簇要更加均匀。
我们可以通过计算 ARI 来度量凝聚聚类和 k 均值给出的两种数据划分是否相似:
print("ARI: {:.2f}".format(adjusted_rand_score(labels_agg, labels_km)))ARI: 0.09
ARI 只有 0.09,说明 labels_agg 和 labels_km 这两种聚类的共同点很少。这并不奇怪,原因在于以下事实:对于 k 均值,远离簇中心的点似乎没有什么共同点。
下面,我们可能会想要绘制树状图(图 3-45)。我们将限制图中树的深度,因为如果分支到 2063 个数据点,图像将密密麻麻无法阅读:
linkage_array = ward(X_pca)
# 现在我们为包含簇之间距离的linkage_array绘制树状图
plt.figure(figsize=(20, 5))
dendrogram(linkage_array, p=7, truncate_mode='level', no_labels=True)
plt.xlabel("Sample index")
plt.ylabel("Cluster distance")
plt.tight_layout()
plt.savefig('Images/03Clustering-20.png', bbox_inches='tight')
plt.show()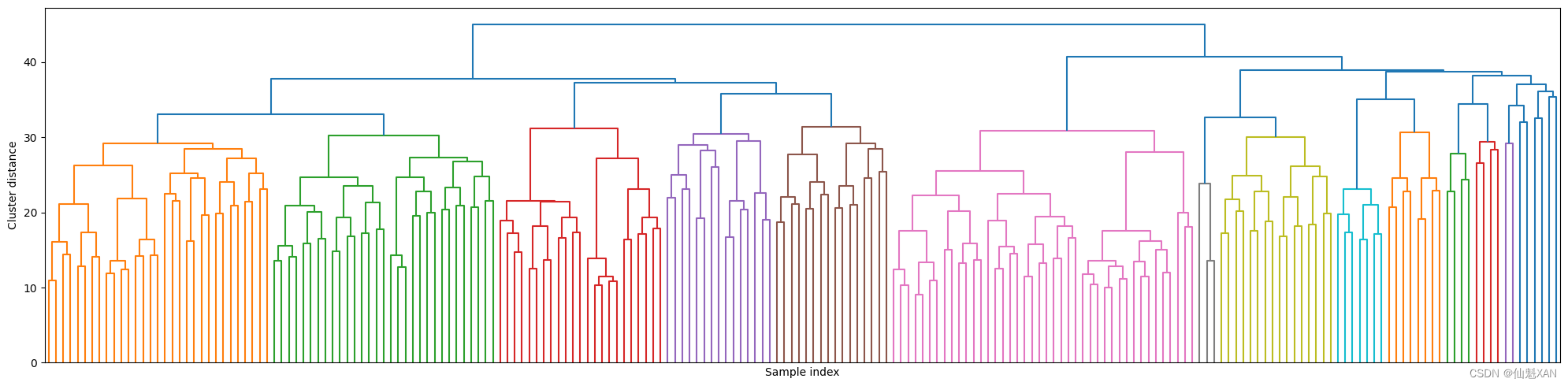
要想创建 10 个簇,我们在顶部有 10 条竖线的位置将树横切。在图 3-36 所示的玩具数据的树状图中,你可以从分支的长度中看出,两个或三个簇就可以很好地划分数据。对于人脸数据而言,似乎没有非常自然的切割点。有一些分支代表更为不同的组,但似乎没有一个特别合适的簇的数量。这并不奇怪,因为 DBSCAN 的结果是试图将所有的点都聚类在一起。
我们将 10 个簇可视化,正如之前对 k 均值所做的那样(图 3-46)。请注意,在凝聚聚类中没有簇中心的概念(虽然我们计算平均值),我们只是给出了每个簇的前几个点。我们在第一张图像的左侧给出了每个簇中的点的数量:
n_clusters = 10
for cluster in range(n_clusters):
mask = labels_agg == cluster
fig, axes = plt.subplots(1, 10, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(15, 8))
axes[0].set_ylabel(np.sum(mask))
for image, label, asdf, ax in zip(X_people[mask], y_people[mask],
labels_agg[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title(people.target_names[label].split()[-1],
fontdict={'fontsize': 9})
虽然某些簇似乎具有语义上的主题,但许多簇都太大而实际上很难是均匀的。为了得到更加均匀的簇,我们可以再次运行算法,这次使用 40 个簇,并挑选出一些特别有趣的簇(图 3-47):
# 用ward凝聚聚类提取簇
agglomerative = AgglomerativeClustering(n_clusters=40)
labels_agg = agglomerative.fit_predict(X_pca)
print("cluster sizes agglomerative clustering: {}".format(np.bincount(labels_agg)))
n_clusters = 40
for cluster in [10, 13, 19, 22, 36]: # 手动挑选“有趣的”簇
mask = labels_agg == cluster
fig, axes = plt.subplots(1, 15, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(15, 8))
cluster_size = np.sum(mask)
axes[0].set_ylabel("#{}: {}".format(cluster, cluster_size))
for image, label, asdf, ax in zip(X_people[mask], y_people[mask],
labels_agg[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title(people.target_names[label].split()[-1],
fontdict={'fontsize': 9})
for i in range(cluster_size, 15):
axes[i].set_visible(False)cluster sizes agglomerative clustering: [139 35 23 2 111 39 106 33 5 161 60 41 70 17 30 20 134 40 23 38 56 264 4 35 44 16 29 135 25 37 42 34 3 17 31 3 21 27 76 37]

5、聚类方法小结
本节的内容表明,聚类的应用与评估是一个非常定性的过程,通常在数据分析的探索阶段很有帮助。我们学习了三种聚类算法:k 均值、DBSCAN 和凝聚聚类。这三种算法都可以控制聚类的粒度(granularity)。k 均值和凝聚聚类允许你指定想要的簇的数量,而 DBSCAN 允许你用 eps 参数定义接近程度,从而间接影响簇的大小。三种方法都可以用于大型的现实世界数据集,都相对容易理解,也都可以聚类成多个簇。
每种算法的优点稍有不同。k 均值可以用簇的平均值来表示簇。它还可以被看作一种分解方法,每个数据点都由其簇中心表示。DBSCAN 可以检测到没有分配任何簇的“噪声点”,还可以帮助自动判断簇的数量。与其他两种方法不同,它允许簇具有复杂的形状,正如我们在 two_moons 的例子中所看到的那样。DBSCAN 有时会生成大小差别很大的簇,这可能是它的优点,也可能是缺点。凝聚聚类可以提供数据的可能划分的整个层次结构,可以通过树状图轻松查看。
附录
一、参考文献
参考文献:[德] Andreas C. Müller [美] Sarah Guido 《Python Machine Learning Basics Tutorial》