目录
树概述
二叉搜索树概述
概念
特性
元素操作
插入
删除
模拟实现
框架
查找
插入
删除
树概述
树——在计算机中是一种很常见的数据结构。
树是一种很强大的数据结构,数据库,linux操作系统管理和windows操作系统管理所有文件的结构就是一颗树形结构
每个树有且只有一个根节点——根节点个数只有一个,节点可存储数据。
根节点往下可以有多个叶子节点,每个叶子节点也可以有多个叶子节点
如下图
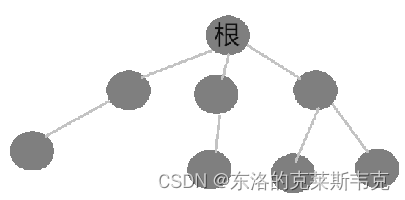
每一个节点都可以是父亲节点,每个父亲节点的叶子节点都是孩子节点
根节点的深度为0,最后一层节点的深度为lgN
如果每一层深度的孩子节点的个数小于等于2,便是二叉树
左边的节点称为左孩子节点,右边的节点称为右孩子节点
如下图
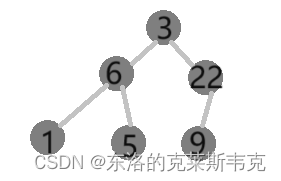
如何正确的看一颗二叉树呢?
3是根节点,6作为3的左孩子也可以是一颗子树,这颗树是以6为根节点的树,也是3的左子树。以22为根节点来作为3的右子树也是一样的。
最小的子树是左孩子和右孩子都为空的叶子节点。
也就是说每一个节点都可以作为根节点,从而成为父亲节点的子树,子树又可以拆成子树,直到左右都为空的叶子节点为止(叶子节点也可以看作一颗子树)。
遍历一颗树应该用递归的思维,如下是遍历顺序
二叉树前序遍历:根 ——> 左子树——>右子树
二叉树中序遍历:左子树——>根——>右子树
二叉树后序遍历:左子树——>右子树——>根
二叉树层序遍历:一条龙遍历,可参考【C++】详解STL的适配器容器之一:优先级队列 priority_queue-CSDN博客
二叉搜索树概述
概念
二叉搜索树是一种二叉树结构,二叉搜索树存储数据时需要符合如下规则(搜索树是支持泛型的,为了方便理解,小编以int类型为例):
左孩子节点的值 < 父亲节点的值 < 右孩子节点的值
如下示例:
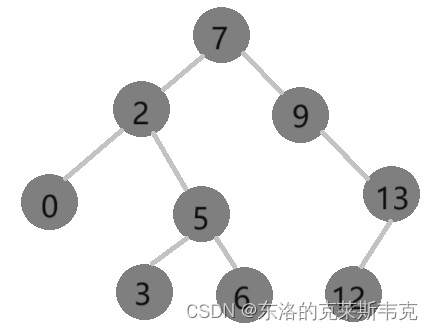
特性
对于所有数据而言,
从整棵树的根节点开始,不断地找左子树,没有左孩子的左子树存的值最小
从整棵树的根节点开始,不断地找右子树,没有右孩子的右子树存的值最大
如果整棵树走中序遍历则是升序
那么用搜索二叉树找一个节点的效率如何呢?
查找的规则很简单,比根节点的值大往右子树走,比根节点的值小往左子树走。每查找一次就能“砍”掉一半数据,只需要查找次。类似于二分查找。
上述查找条件是:整棵树基本符合二叉树结构。如果是比较极端的结构,效率会接近。比如下述结构
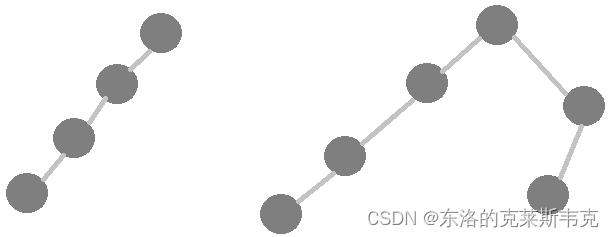
二叉搜索树搜索的效率的上限很高,下限很低。
元素操作
插入
二叉搜索树中不允许有相等的值存在,因为要维持 “左树的值小于根小于右数的值” 这一特性。
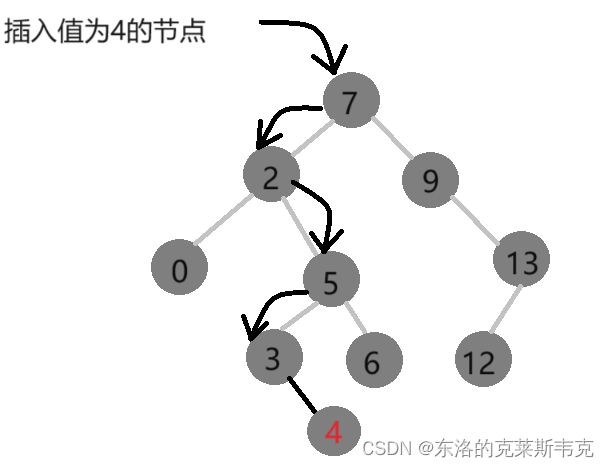
如果要插入的值在树中不存在,这个值会插入到中间某个位置吗?
答案是不会,因为这个值一定会从整棵树的根节点比到叶子节点,然后插入到叶子节点的后面。如下示意图:
删除
删除的情况比较复杂,大致可以分为两种情况
孩子节点的个数是1或0
假设被删节点为cur,被删节点的父亲节点为fatherNode。
先找是否有cur,找不到,删除失败。
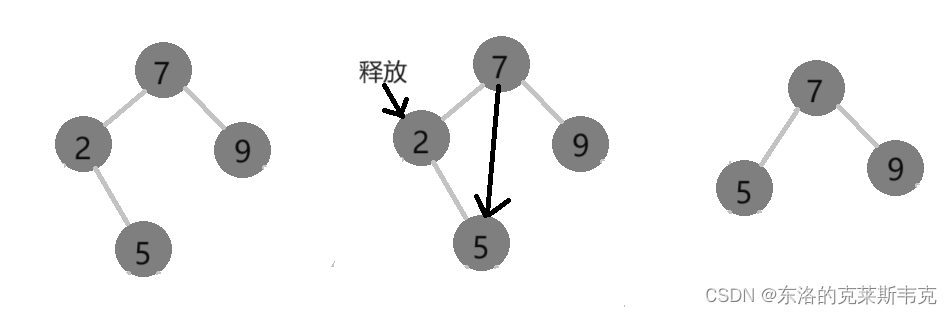
找到了,判断cur是fatherNode的左孩子还是右孩子
是左孩子,让fatherNode的左指针指向cur的孩子节点
是右孩子,让fatherNode的右指针指向cur的孩子节点
如果没有孩子节点,则fatherNode的指针指向空
改变指向关系后整棵树就没有cur节点了,最后释放cur的内存
fatherNode的左孩子被删应该有新的左孩子接替,右孩子应该有新的右孩子接替,这样才不会破坏二叉搜索树的结构,所以要判断cur是fatherNode的左孩子还是右孩子
孩子节点的个数是2
孩子节点是1或0的时候只需改变指向关系,然后再释放被删节点的内存即可。
那么被删节点的孩子个数是两个的时候还能这么做吗?
显然是不能的,因为一个父亲节点最多只能有两个孩子节点。
删除孩子节点的个数是2的节点,最核心的思想是:
被删节点为cur,但不直接删cur这个节点,因为这样会破坏这颗树的结构。
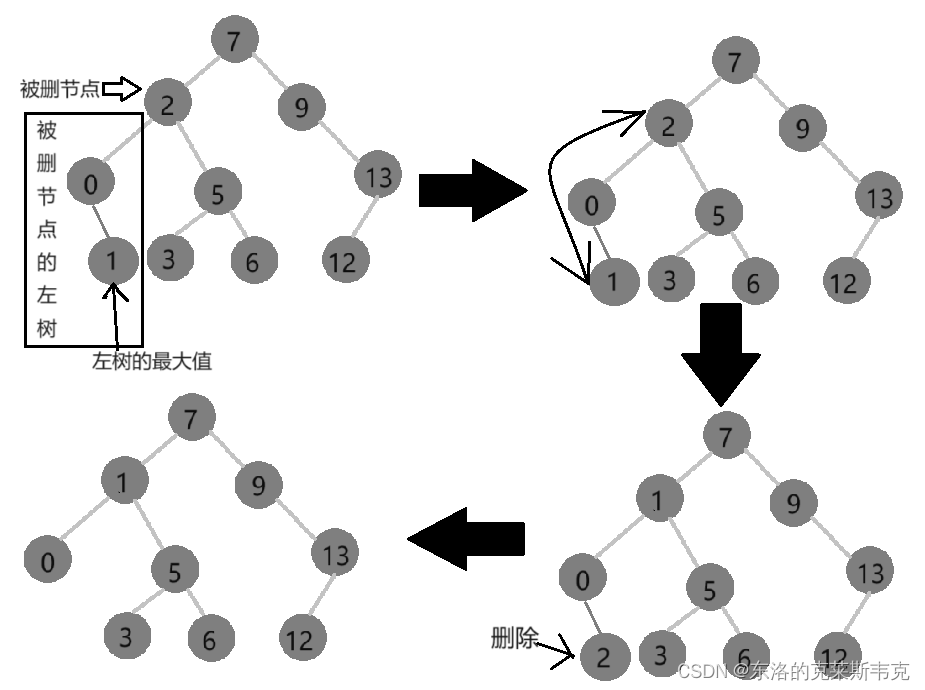
找一个孩子节点为1或0的节点为leftMax_Node,让leftMax_Node节点的值和cur节点的值交换,然后删leftMax_Node节点
通过替换的方法就完成了cur节点的删除
那么怎么找孩子节点为1或0的节点呢?
左子树的最大节点或右子树的最小节点
注意:是被删节点cur的左树(右树),而不是整棵树的左树(右树)
在上文二叉树的特性中已经提过,找最大值或最小值,找的一定是叶子节点
整个二叉搜索树中,左子树存小值,右子树存大值。
如果选左子树的最大值放在根节点的位置,依旧符合左子树的值小于根小于右子树这一规则,删掉该节点不会破坏二叉树的结构。
左子树的最大节点或右子树的最小节点是完美的 “替罪羊”
模拟实现
模板相关知识可参考:
【C++】详解C++的模板-CSDN博客
内存管理相关知识可参考:
【C++】C++的内存管理-CSDN博客
框架
节点的设计
有两个指针指向左右孩子
在用一个变量存值
template <class K>
class BSNode
{
public:
BSNode(const K& Key = K())
:_left(nullptr)
,_right(nullptr)
,_key(Key)
{
}
BSNode<K>* _left;
BSNode<K>* _right;
K _key;
};二叉搜索树的设计
只需要一个节点指针指向整棵树的根节点即可
template <class K>
class BSTree
{
typedef BSNode<K> node;
//......
private:
node* _root;
};
查找
查找的代码很简单,小编就不细讲了。
有一点要提醒大家,大家一定要用判断语句把查找条件分开,比根大就往右树查找,比根小就往左树查找。千万不要写成暴力查找——不管值的大小,遍历整棵树
代码如下
bool _FindNode(node* root, const K& key)
{
while (root)
{
if (root->_key < key)
{
root = root->_right;
}
else if (root->_key > key)
{
root = root->_left;
}
else
{
return false;
}
return true;
}
}可以把上述代码设计成私有,再封装一层共有的函数,这样做的意义是不用传节点的指针了
bool FindNode(const K& key)
{
return _FindNode(_root, key);
}插入
接口
bool Insert(const K& key) 首先应该判断整棵树是否为空,如果为空,直接让_root直接指向新节点
if (_root == nullptr) //如果为空
{
_root = new node(key); //头节点指针指向新节点
return true;
}二叉搜索树是不允许有重复的值出现的
应该再写一遍查找的逻辑,因为_root是指向整棵树的根的,所以需要定义一个临时指针,当我们找到相等的值时,插入失败。
node* cur = _root;
node* fatherNode = nullptr;
while (cur)
{
if (cur->_key < key) //插入的元素比当前节点的值大,
{
fatherNode = cur; //记录父亲节点的指针
cur = cur->_right; //往右树找
}
else if (cur->_key > key)
{
fatherNode = cur;
cur = cur->_left;
}
else
{
return false;
}
}没找到的话,说明临时指针已经找到空了,临时指针的父亲节点就是合适的叶子节点了,插在叶子节点的孩子位置即可,是左孩子还是右孩子需要和父亲节点比较大小
node* newNode = new node(key);
if (fatherNode->_key < key)//判断要插入父亲节点的左边还是右边
{
fatherNode->_right = newNode;
}
else
{
fatherNode->_left = newNode;
}删除
接口
bool Erase(const K& key) 先判断是否是空树
if (nullptr == _root)//如果是空树,删除失败
{
return false;
}和插入类似,要判断被删的节点是否存在
node* cur = _root; //临时变量,cur是指要删除的节点
node* fatherNode = nullptr; //cur的父亲节点,
while (cur)//找要删除的节点
{
if (cur->_key < key)
{
fatherNode = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
fatherNode = cur;
cur = cur->_left;
}
else
{
break;
}
}if (nullptr == cur) //没找到要删除的节点,删除失败
{
return false;
}下面就是要删除节点的逻辑了,上文已经讲了删除的原理,这里细讲代码细节
孩子节点数量为1或0
节点的孩子树不管是1还是0,可以只写左孩子为空的情况和右孩子为空的情况,左右孩子都为空的情况可以不写。
因为左右孩子都为空的情况,可以走左孩子为空的逻辑,只是指向新节点还是指向空的问题。
if (cur->_left == nullptr) //要删除的节点左为空
{
if (cur == _root) //极端情况,
{
_root = cur->_right;
delete cur;
return true;
}
if (fatherNode->_left == cur) //判断要删除的节点在父亲节点的左边还是右边
fatherNode->_left = cur->_right;
else //改变指向
fatherNode->_right = cur->_right;
delete cur; //删除
return true;
}
else if (cur->_right == nullptr)//要删除的节点右为空
{
if (cur == _root) //极端情况
{
_root = cur->_left;
delete cur;
return true;
}
if (fatherNode->_left == cur) //判断要删除的节点在父亲节点的左边还是右边
fatherNode->_left = cur->_left;
else //改变指向
fatherNode->_right = cur->_left;
delete cur; //删除节点
return true;
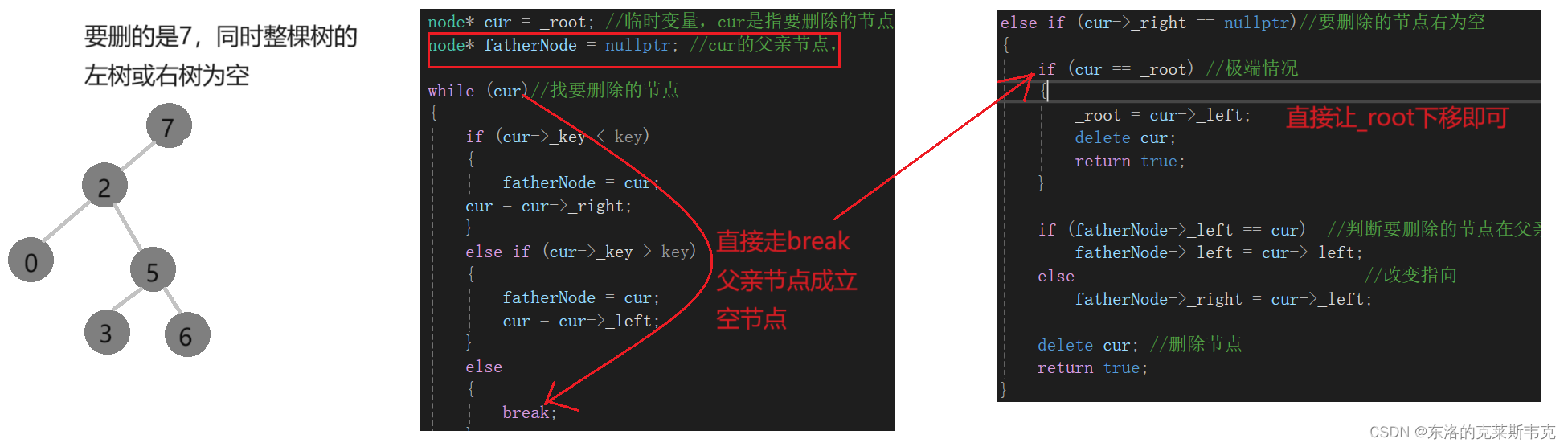
}极端情况做了特殊处理
极端情况如下图所示
孩子节点数量为2
else //要删除的节点左右都不为空
{
node* leftMax_Node = cur->_left; //左树最大节点 (被删节点的左树)
node* leftMax_FatherNode = cur; //左树最大节点的父亲节点
while (leftMax_Node->_right) //找代替节点,左树的最右节点(找左树的最大值)
{
leftMax_FatherNode = leftMax_Node;
leftMax_Node = leftMax_Node->_right;
}
std::swap(cur->_key, leftMax_Node->_key); //交换完之后,左树的最大节点就是要删的值了
if (leftMax_FatherNode->_left == leftMax_Node) //要判断被删节点是父亲节点的左孩子还是右孩子
leftMax_FatherNode->_left = leftMax_Node->_left;
else
leftMax_FatherNode->_right = leftMax_Node->_left;
delete leftMax_Node;
return true;
}