关于图的遍历实际上就两种

广度优先和深度优先，一般关于图的遍历都是基于邻接矩阵的，考试这些，用的也是邻接矩阵。

本篇文章先介绍广度优先遍历的原理，和代码实现

什么是图的广度优先遍历？

这其实和二叉树的层序遍历非常相似，大家都喜欢看例子，那我就举例子：

若对这个无向图，从A节点开始进行广度优先遍历：

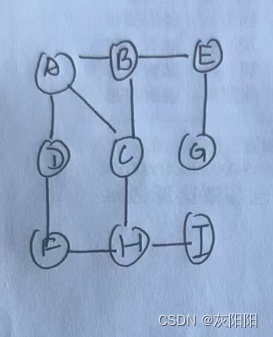
那么它的顺序就应该是：

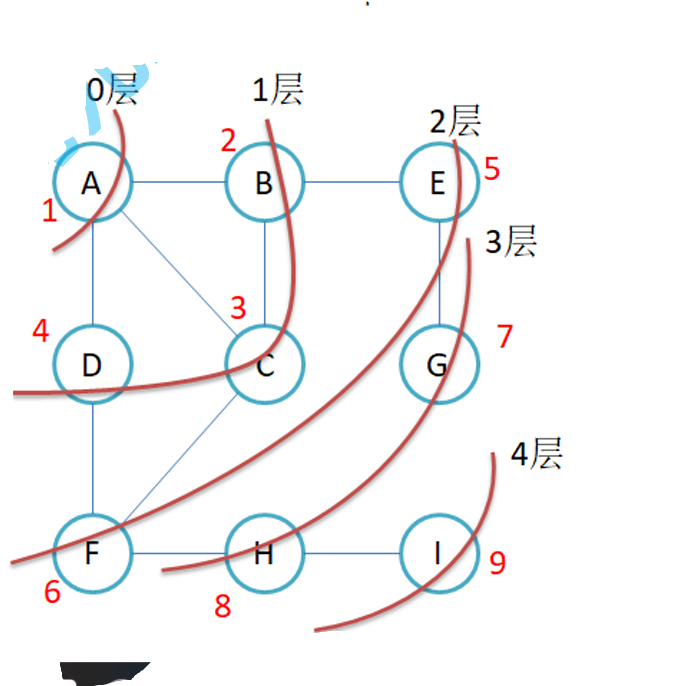
遍历方式：

借助队列queue，以及一个boolean类型的数组arr，用来记录顶点是否已经访问：

 public void traverse(char v){//需要的顶点

        Queue<Character> queue=new LinkedList<>();

        /*
        * vertexS是储存所有顶点的字符数组
        * _getIndexOfV(传入一个字符（顶点）)---->这个函数可以获得对应vertexS数组的下标
        * 
        * */
        boolean[] visited=new boolean[vertexS.length];//定义，用来标记是否已近访问
        queue.offer(v);

        while(!queue.isEmpty()){
            char vertex= queue.poll();//出队列，一个
            System.out.print(vertex);//直接打印
            int index=_getIndexOfV(vertex);//获得下标
            visited[index]=true;//出队列就要置为空

            for (int i = 0; i < vertexS.length ; i++) {//遍历第index行的（在当前顶点周围搜索是否有顶点链接）
                if(matrix[index][i]!=0&&!visited[i]){
                    queue.offer(vertexS[i]);//入队列
                    visited[i]=true;//入队就要标记，免得等一下重复入队，造成严重后果
                }
            }

            if(!queue.isEmpty()){//不为空就加一个箭头
                System.out.print(" -> ");
            }
        }

    }

以这个图作为测试：

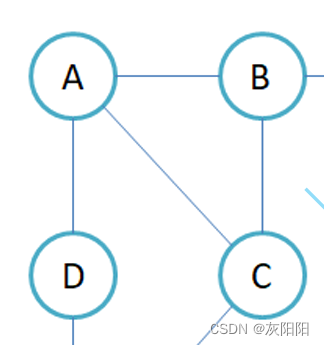
public class Test {

    public static void main(String[] args) {
        char[] array = {'A', 'B', 'C', 'D','E'};
        GrapByMatrix grap = new GrapByMatrix(array, false);
        grap.addEdge('A', 'B', 1);
        grap.addEdge('A', 'D', 1);
        grap.addEdge('B', 'C', 1);
        grap.addEdge('A', 'C', 1);



        grap.traverse('A');
    }
}

执行结果：