1.题目

如下图所示的螺旋折线经过平面上所有整点恰好一次。

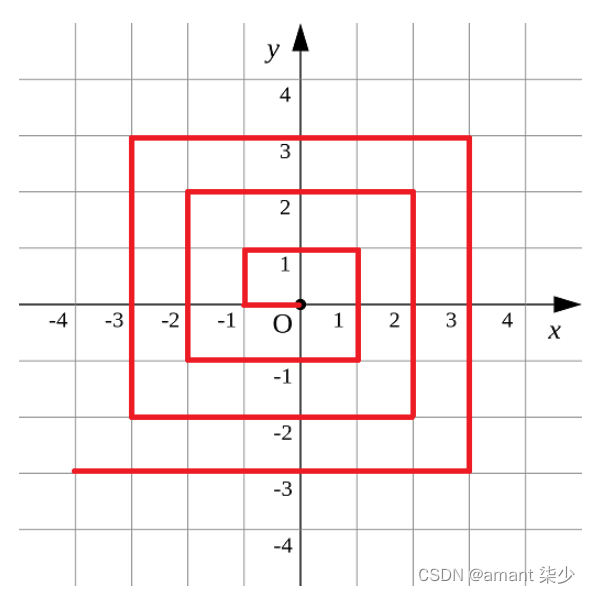
对于整点 $(X,Y)$，我们定义它到原点的距离 $dis(X,Y)$ 是从原点到 $(X,Y)$ 的螺旋折线段的长度。

例如 $dis(0,1)=3,dis(-2,-1)=9$

给出整点坐标 $(X,Y)$，你能计算出 $dis(X,Y)$ 吗？

输入格式
包含两个整数 X,Y。

输出格式
输出一个整数，表示 dis(X,Y)。

数据范围
$-10^9\le X,Y\le 10^9$

输入样例：

0 1

输出样例：

3

2.基本思想

① 模拟 TLE!
② 每次走一条边 O（10^9） TLE!
③找规律 O（1）
根据（x，y） 判断在哪个方向的边上，其次找出特殊点（起点） 最后 加上 偏移量即可

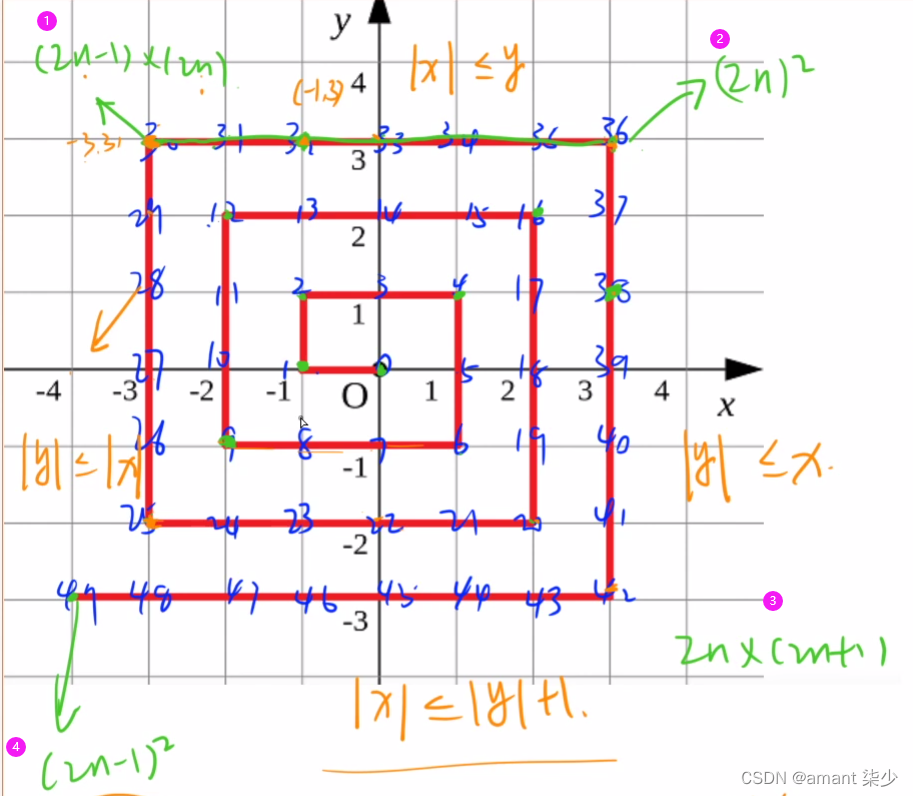
④优雅做法：找规律可以发现每层的右上角点所需步数为为4k²，求任意一个点的dis首先找到这个点所在的层数

• 如果在该层的左或上则减去该点到右上角曼哈顿距离，
• 如果在该层的右或下则加上该点到右上角曼哈顿距离，；

3.代码实现

找规律  O(1)

import java.util.Scanner;

public class Main {
    static Scanner sc = new Scanner(System.in);

    public static void main(String[] args) {
        long x = sc.nextInt();
        long y = sc.nextInt();

        if (Math.abs(x) <= y) {//在上方
            long n = y;
            System.out.println((long) (2*n-1)*(2*n)+x-(-n));  // 特殊点为起点 加 偏移量
        } else if (Math.abs(y) <= x) {  // 在右方
            long n = x;
            System.out.println((long) (2*n)*(2*n)+n-y);
        } else if (Math.abs(x) <= Math.abs(y) + 1 && y<0) { //在下方
            long n = Math.abs(y);
            System.out.println((long) (2*n)*(2*n+1)+n-x);
        } else {  // 作左方
            long n = Math.abs(x);
            System.out.println((long) (2*n-1)*(2*n-1)+y-(-n+1));
        }
    }
}

优雅做法

import java.util.Scanner;

public class _1237螺旋折线 {
    static Scanner sc = new Scanner(System.in);

    public static void main(String[] args) {
        int x = sc.nextInt(), y = sc.nextInt();
        long k = Math.max(x, y);//
        if (x >= y) System.out.println(4 * k * k + Math.abs(x - k) + Math.abs(y - k));//y=x 之下
        else System.out.println(4 * k * k - Math.abs(x - k) - Math.abs(y - k));//y=x 之上
    }
  }