146.LRU 缓存

. - 力扣（LeetCode）

请你设计并实现一个满足  LRU (最近最少使用) 缓存 约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。 

思路：双向链表+一个哨兵节点，使用map记录（key，node）

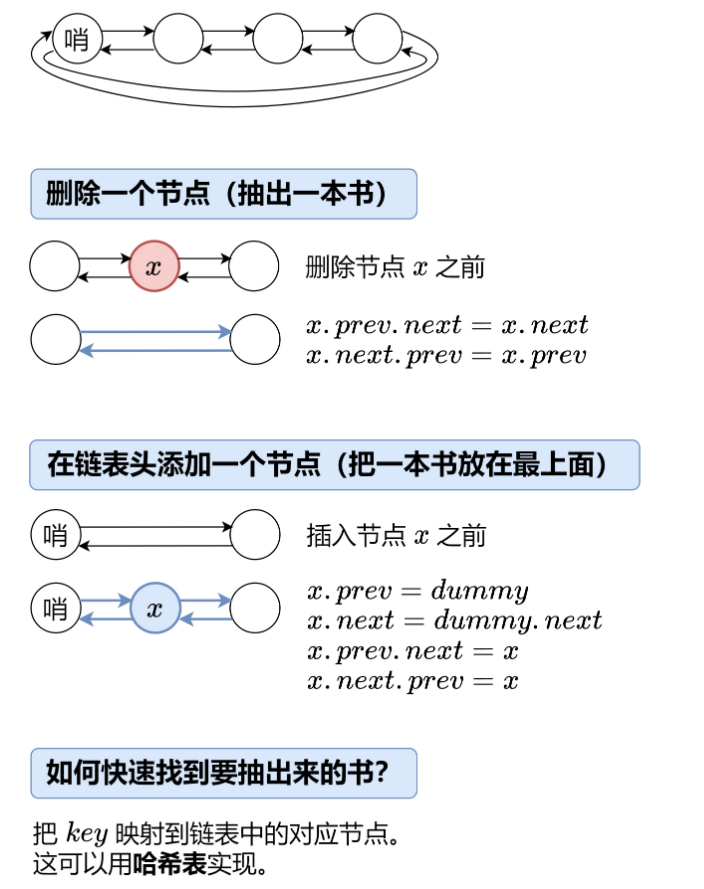
（图和思路都是偷力扣大佬的） 

实现：

class Node {
    constructor(key, value) {
        this.key = key
        this.value = value
        this.pre = null
        this.next = null
    }
}

class LRUCache {
    constructor(capacity) {
        this.capacity = capacity
        this.dummy = new Node()
        this.dummy.next = this.dummy
        this.dummy.pre = this.dummy
        // 哈希表 用来存key和节点node
        this.keyToNodeMap = new Map()
    }
    // 删除x节点
    delete(x) {
        x.pre.next = x.next
        x.next.pre = x.pre
    }
    // 将节点添加在链表头 哨兵节点后
    addTop(x) {
        x.pre = this.dummy
        x.next = this.dummy.next
        x.pre.next = x
        x.next.pre = x
    }
    getNode(key) {
        // 没有该节点
        if (!this.keyToNodeMap.has(key)) { 
            return null;
        }
        // 有 拿出来放在头部
        const node = this.keyToNodeMap.get(key); 
        this.delete(node); 
        this.addTop(node); 
        return node;
    }
    get(key) {
        const node = this.getNode(key)
        return node?node.value:-1
    }
    put(key, value) {
        let node = this.getNode(key)
        // 有这个值 拿出来更新
        if (node) {
            node.value = value
        } else {
            // 新建节点放入
            node = new Node(key, value)
            this.keyToNodeMap.set(key, node)
            this.addTop(node)
            // 判断有没有溢出
            if (this.keyToNodeMap.size > this.capacity) {
                const backNode = this.dummy.pre
                this.keyToNodeMap.delete(backNode.key)
                this.delete(backNode)
            }
        }
    }
}

215.数组中最大的第k个元素

. - 力扣（LeetCode）

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。 

思路：

看的是这位佬的：. - 力扣（LeetCode）

利用大根堆根节点最大的特性，构建大根堆，将根节点与最末尾节点交换，移出这个最大节点，再进行排序。。。

利用的是堆的思想，但实际是用数组来实现的 

顺序存储二叉树的特点：

第 n 个元素的 左子节点 为 2*n+1
第 n 个元素的 右子节点 为 2*n+2
第 n 个元素的 父节点 为 (n-1)/2
最后一个非叶子节点为 Math.floor(arr.length/2)-1

实现：

var findKthLargest = function (nums, k) {
    let len = nums.length
    // 先构建大根堆
    buildMaxHeap(nums, len)
    // 循环 将大根堆根节点和最末尾的节点交换
    // 循环到第k+1个最大就停止 最后返回的nums的根节点就是目标数
    // 这里for循环要用nums.length，不能用len，因为len是会改变的
    for (let i = nums.length - 1; i >= nums.length - k + 1; i--) {
        swap(nums, 0, i) // 将最大节点和最末尾的节点交换
        // 调整大根堆
        maxHeapify(nums, 0, --len) // 移到最后的节点不参与调整
    }
    return nums[0] // 返回第k个最大的值

    // 创建大根堆 自下而上构建大根堆
    function buildMaxHeap(nums, len) {
        // 最小非叶子节点：Math.floor(arr.length/2)-1
        for (let i = Math.floor(len / 2) - 1; i >= 0; i--) {
            maxHeapify(nums, i, len)
        }
    }
    function maxHeapify(nums, i, len) {
        let left = i * 2 + 1 // i的左子节点
        let right = i * 2 + 2 // i的右子节点
        let largest = i // 最大值的节点下标

        // 和左子节点比较
        if (left < len && nums[left] > nums[largest]) {
            largest = left
        }
        // 和右子节点比较
        if (right < len && nums[right] > nums[largest]) {
            largest = right
        }
        if (i !== largest) {
            swap(nums, i, largest) // 将子节点与父节点交换
            maxHeapify(nums, largest, len) // 再继续向下比较
        }
    }
    function swap(nums, a, b) {
        let temp = nums[a]
        nums[a] = nums[b]
        nums[b] = temp
    }

};

 今天写的两道都有点难，对于我这个白痴来说，所以明天还要再写一遍！！！