目录
1.前言
2.list的节点定义和结构
3.list的迭代器定义和结构
4.list的定义和结构
5.list的内存管理
6.list的元素操作
前言
在刨析了vector容器的源码后,list容器相比与vector容器,其元素的插入和删除较快,不需要对原本容器中的元素进行排序,因此针对list容器的每一次插入和删除都是常数级。而且list对于内存的申请属于是需要几个内存就申请几个内容,而vector申请的内存通常为当前内存的两倍。本章将对list进行讲解,至于何时使用vector,何时使用list更是要区别于元素的多少,具体的业务场景。
list的节点定义和结构
list的结构属于环状双向链表的结构(PS:环状双向链表,指的是链表的头指针指向尾节点,链表的尾指针指向头节点,故称环状双向链表),应此在实现list时,我们还需要针对其list中的每一个节点进行设计。在设计list节点时,要实现list双向链表的特性,我们还需要两个指针,一个头指针一个尾指针,且每一个节点需要存储值,故list节点设计代码如下:
//list节点设计代码
template <class T>
struct _list_node{
typedef void* void_pointer;//设计为空指针方便类型转换,也可以设计为_list_node<T>*
void_pointer prev;//头指针
void_pointer next;//尾指针
T data; //存储值
}list的迭代器定义和结构
相比于vector的随机迭代器,list提供的迭代器为双向迭代器,因为list不支持下标操作。而且vector在扩充元素时,若内存空间不足则需要向系统申请新的空间,并把旧元素复制到新的空间上,这会导致迭代器生效(类似于虚吊指针,也可以叫悬空指针)。但是list的插入操作都只是修改节点的头指针和尾指针的指向空间,应此不会导致迭代器生效。在了解list迭代器类型后,其设计的源码如下:
//list的迭代器设计源码
template<class T, class Ref, class Ptr> //Ref代表解引用时返回引用类型,Ptr则是指针类型
struct _list_iterator{
typedef _list_node<T>* link_type; /list节点指针
link_type node; //变量node指向list节点
typedef _List_iterator<T, Ref, Ptr> self; //当前实例对象的别名
typedef _list_iterator<T, T&,T*> iterator; //当前实例对象的迭代器
typedef bidirectional_iterator_tag iterator_category; //封装双向迭代器
//以下为迭代器常用封装,Traits编程方法
typedef T value_tyoe;
typedef Ptr pointer;
typedef Ref reference;
typedef size_t size_type;
typedef ptrdiff_t difference_type;
}在知道list迭代器为双向迭代器后,我们知道双向迭代器的特点,即不支持下标操作,仅支持迭代器的累加,递减,解引用和判断节点值是否相等的特性,为了实现这些特性,其迭代器还需要实现以下功能:
//list迭代器支持的操作的实现
_list_iterator(){}
_list_iterator(link_type x) : node(x){}
_list_iterator(const iterator& x) : node(x.node){}
bool operator==(const self& x) const { //判断是否相等
return node == x.node;
}
bool operator!=(const self& x) const { //判断是否不等
return node != x.node;
}
pointer operator->() const { return &(operator*()); } //取值(左值)
reference operator*() const { return (*node).data; } //取值(右值)
//以下为累加的实现
self& operator++(){
node = (link_type)((*node).next);
return *this;
}
self& operator++(int){
self temp =*this;
++(*this);
return tem;
}
//以下为递减的实现
self& operator--(){
node = (link_type)((*node).prev);
return *this;
}
self& operator--(int){
self tmp = *this;
--(*this);
return tmp;
}list的定义和结构
在了解list节点和迭代器的定义和结构后,我们还提到list是一种环状的双向链表,而由于独特的环状结构,我们在设计该双链表时需要插入一个空的节点(PS:是为了满足STL的前闭后开的要求,但是我觉得更多的是为了方便判断是否遍历完整个链表而设计的节点)。在满足设计的结构的基础上,我们在实现list的结构时,还需要定义形如begin(),end(),empty(),size(),font()和back()等操作函数,故list结构大致如下:
//list的结构实现
template<class T, class Alloc = alloc>
class list{
protected:
typedef _list_node<T> list_node;
typedef simple_alloca<list_node,Alloc> list_node_allocator;//封装迭代器,内存管理中使用
public:
typedef list_node* link_type;
protected:
link_type node; //节点指针,指向链表的头节点便可表示整个链表
}
iterator begin() { return (link_type)((*node).next); } //获取头节点
iterator end() { return node; } //获取尾节点
bool empty() const { return node->next == node; } //判断是否为空节点
size_type size() const{ //计算容器中元素的个数
size_type result = 0;
distance(begin(), end(), result);//遍历容器
return result;
}
reference front() { return *begin(); } //取头节点的值
rederence back() { return *(--end()); } //取尾节点的值针对list的环状双向链表,可以参考下图:
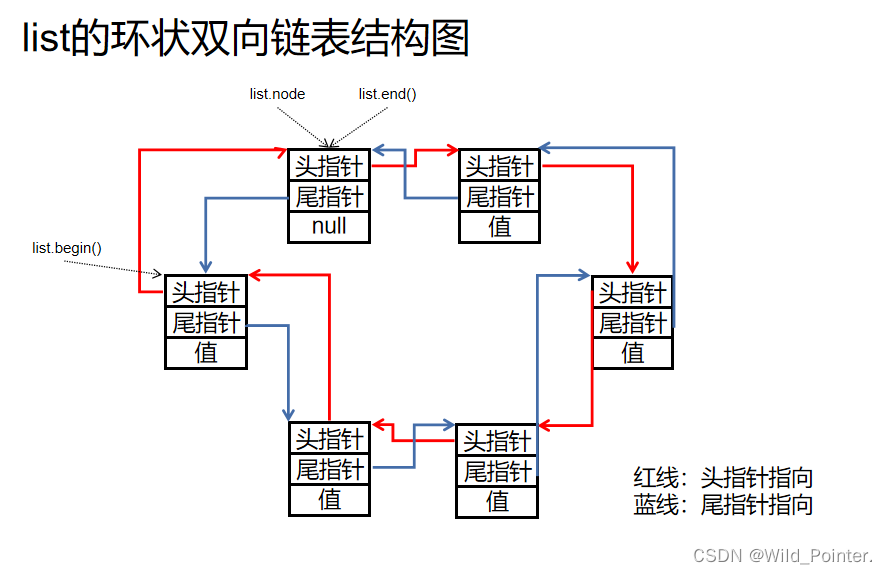
图1.listD的环状双向链表结构图
list的内存管理
参考vector容器的讲解,其list内部也存在应该迭代器,为了实现内存的精准控制,其迭代器也是专门定义了一个(参考小节:list的迭代器定义和结构),为了实现内存的管理,我们需要满足内存的分配,释放等操作,在这些操作基础上还需要满足带值的节点的内存申请,对此list于内存相关的代码如下:
//list内存管理源码实现
link_type get_node(){ return list_node_allocator::allocate(); } //申请一个节点
link_type put_node(link_type p){ return list_node_allocator::deallocate(p); }//释放一个节点
link_type create_node(const T& x){ //申请一个带值的节点
link_type p = get_node();
construct(&p->data,x); //构造函数
return p;
}
link_type destroy_node(link_type p){ //销毁一个带值的节点
destroy(&p->data);
put_node(p);
}
list() { empty_initialize(); } //list构造函数,用于产生一个空链表
void empty_initialize(){ //产生一个空节点
node = get_node();
node->next = node;
noed->prev = node;
}list的元素操作
形如vector,list也提供了许多元素操作的函数,如insert(),push_back(),erase()和uniques()函数等操作,本小节将对这些元素操作进行源码的讲解,如下:
1.insert()函数实现源码:
//inser()用于在指定位置前插入元素
iterator inser(iterator position, const T& x){
link_type tmp = create_node(x); //初始化带值节点
//调整当前插入节点的指针指向
tmp->next = position.node;
tmp->prev = position.node->prev;
//调整迭代器指向节点的指针指向
(link_type(position.node->prev))->next = tmp;
position.node->prev = tmp;
return tmp;
}2.push_front()函数实现源码:
//push_front()用于插入一个节点作为头节点
void push_front(const T& x){
insert(begin(),x);
}3.push_back()函数实现源码:
//push_back()函数用于插入一个节点作为尾节点
void push_back(const T& x){
insert(end(),x);
}4.erase()函数实现源码:
//erase()函数用于移除指定节点
iterator erase(iterator position){
link_type next_node = link_type(position.node->next); //获取头指针指向的节点
link_type prev_node = link_type(position.node->prev); //获取尾指针指向的节点
//更新移除节点的前后节点指针的指向
prev_node->next = next_node;
next_node->prev = prev_node;
destory_node(position.node); //释放当前节点
return iterator(next_node); //返回移除节点的上一个节点指针
}5.pop_front()函数实现源码:
//pop_front()函数用于移除头节点
void pop_front(){
rease(begin());
}6.pop_back()函数实现源码:
//pop_back()函数用于移除尾节点
void pop_back(){
iterator tmp = end();
rease(--tmp);
}
//因为真实的尾节点其值为空,参考环状双向链表结构体
//所以先获取尾节点后,再移动指针指向带有值的最后一个节点,最后释放该节点7.clear()函数实现源码:
//clear()函数用于清除所有节点
template<class T , class Alloc>
void list<T,Alloc>::clear(){
link_type cur = (link_type) node->next; //获取链表头节点
while(cur != node){ //遍历链表中的节点
link_type tmp = cur;
cur = (link_type) cur->next;//更新为下一个节点
destroy_node(tmp);
}
//恢复node状态
node->next = node;
node->prev = node;
}8.remove()函数实现源码:
//remove()函数用于移除指定值的所有节点
template<class T, class Alloc>
void list<T,Alloc>::remove(const T& value){
iterator first = begin(); //获取头节点
iterator lase = end(); //获取尾节点
while(first != lase){ //遍历所有节点
iterator next = first;
++next; //获取下一个节点
if(*first == value) erase(first);
first = next;
}
}9.unique()函数实现源码:
//unique()函数用于移除数值相同的连续元素(最后剩余一个)
template<class T, class Alloc>
void list<T,Alloc>::unique(){
iterator first = begin();
iterator lase = end();
if(first == last) teturn; //空链表则退出
iterator next = first;
while(++next != last){ //遍历所有节点
if(*first == *next)
erase(next);
else
first = next;
next = first;
}
}10.transfer()函数实现源码:
//transfer()函数用于将指定范围内的节点移动到指定节点的前面
void transfer(iterator position, iterator first, iterator last){
//position:指定节点 first:范围的头节点 last:范围的尾节点(不包含至移动的范围中)
if(position != last){
(*(link_type((*last.node).prev))).next = position.node;
(*(link_type((*first.node).prev))).next = last.node;
(*(link_type((*position.node).prev))).next = first.node;
link_type tmp = link_type((*position.node).prev);
(*position.node).prev = (*last.node).prev;
(*last.node).prev = (*first.node).prev;
(*first.node).prev = tmp;
}
}11.splice()函数实现源码:
//splice()函数用于将指定的两个链表结合
void splice(iterator position, list& x){
if(!x.empty()){ //判断链表是否为空
transfer(position,x.begin(),x.end());
}
}
void splice(iterator position, list& x, iterator i){
iterator j = i;
++j;
if(position == i || position == j) return; //当前链表只存在一个节点
transfer(position,i,j);
}
void splice(terator position, list& x, iterator first, iterator last){
if(first != last)
transfer(position,first,last)
}11.merge()函数实现源码:
//merge()函数用于合并两个递增的链表,最后链表元素排序也为递增
template<class T, class Alloc>
void list<T,Alloc>::merge(list<T,Alloc>& x){
iterator first1 = begin();
iterator last1 = end();
iterator first2 = x.begin();
iterator last2 = x.end();
while(first1 != last1 && first2 != last2){ //遍历次数为最短的链表元素个数
if(*first2 < *first1){ //当链表1的值大于链表2
iterator next = first2;
transfer(first1,first2,++next);
first2 = next;
}
else{
++first1;
}
if(first2 != last2) { transfer(last,first1,first2); } //如果链表没有插入完,则合并
}
}12.reverse()函数实现源码:
//reverse()函数用于见元素逆向排序
template<class T, class Alloc>
void list<T,Alloc>::reversr(){
if(node->next == node || link_type(node->next)->next == node) return; //链表节点为1或0
iterator first = begin();
++first;
while(first != end()){ 遍历整个链表
iterator old = first;
++first;
transfer(begin(),old,first); //把头节点到old节点转移到链表前
}
}
13.sort()函数实现源码:
//sort()函数用于对链表进行排序
template <class T, class Alloc>
void list<T, Alloc>::sort() {
if(node->next == node || link_type(node->next)->next == node) return;//链表节点个数为0或1
list<T, Alloc> carry; //临时存储链表节点
list<T, Alloc> counter[64];
int fill = 0;
while (!empty()) {
carry.splice(carry.begin(), *this, begin());
int i = 0;
while(i < fill && !counter[i].empty()) {
counter[i].merge(carry);
carry.swap(counter[i++]);
}
carry.swap(counter[i]);
if (i == fill) ++fill;
}
for (int i = 1; i < fill; ++i) counter[i].merge(counter[i-1]);
swap(counter[fill-1]);
}





![页面加载不出来,报错[@umijs/runtime] load component failed](https://img-blog.csdnimg.cn/direct/a8128ccc9b7b42c3ae50ba83aeecf5d1.png)