前言:
经过前面的学习,我们接下来要开始二叉树的学习,因二叉树有难度,为了方便讲解以及各位的理解,本节知识会分成不同的小节进行学习,在本阶段只学习初阶的二叉树(堆,二叉数基本知识,二叉树的实现以及OJ题等),在学习了C++中会学习进阶的二叉树如:AVL树,红黑树等,敬请期待吧!本次学习的是二叉树的基本知识点。注:每小节内容都很重要,还望各位读者不要松懈,随着本博主一起努力学习吧!
一、树的概念
树,大家都见过,如果我们仔细观察的话会发现以下特点:对于大多数的树来说,其枝条都会汇与一点,一个枝条可能有其它枝条也可能没有对吧。有句话是这样说的:艺术来源于生活。数据结构的命名也不例外。既然它敢起名叫树,那么肯定会与树有相似点。要是没有的话,那为什么不叫其它名字?那么,问题来了?那些相似点体现在哪里?大家可以先想象一下:你心目中树的数据结构长什么样?给你两幅图,你选则哪一副?
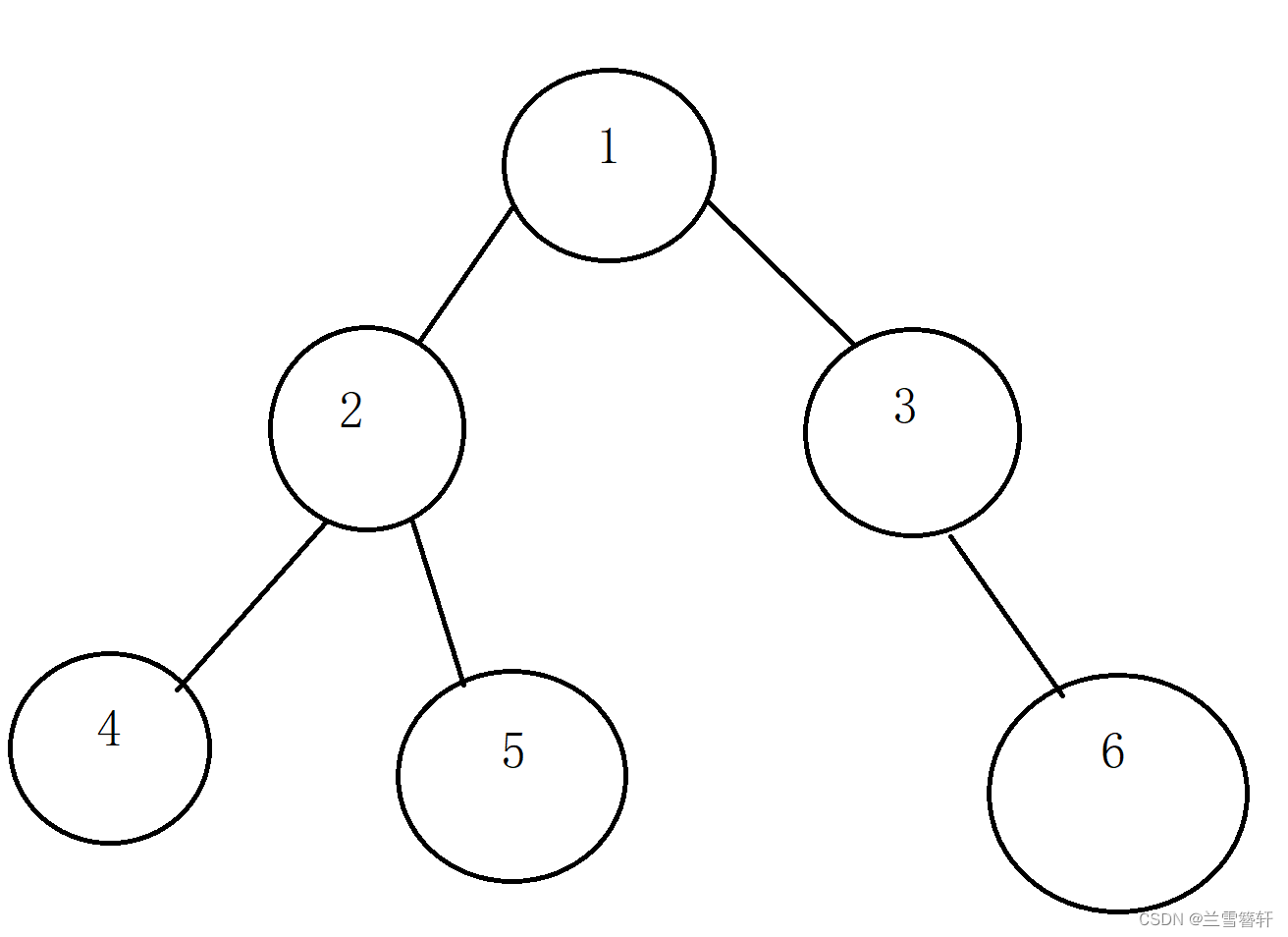
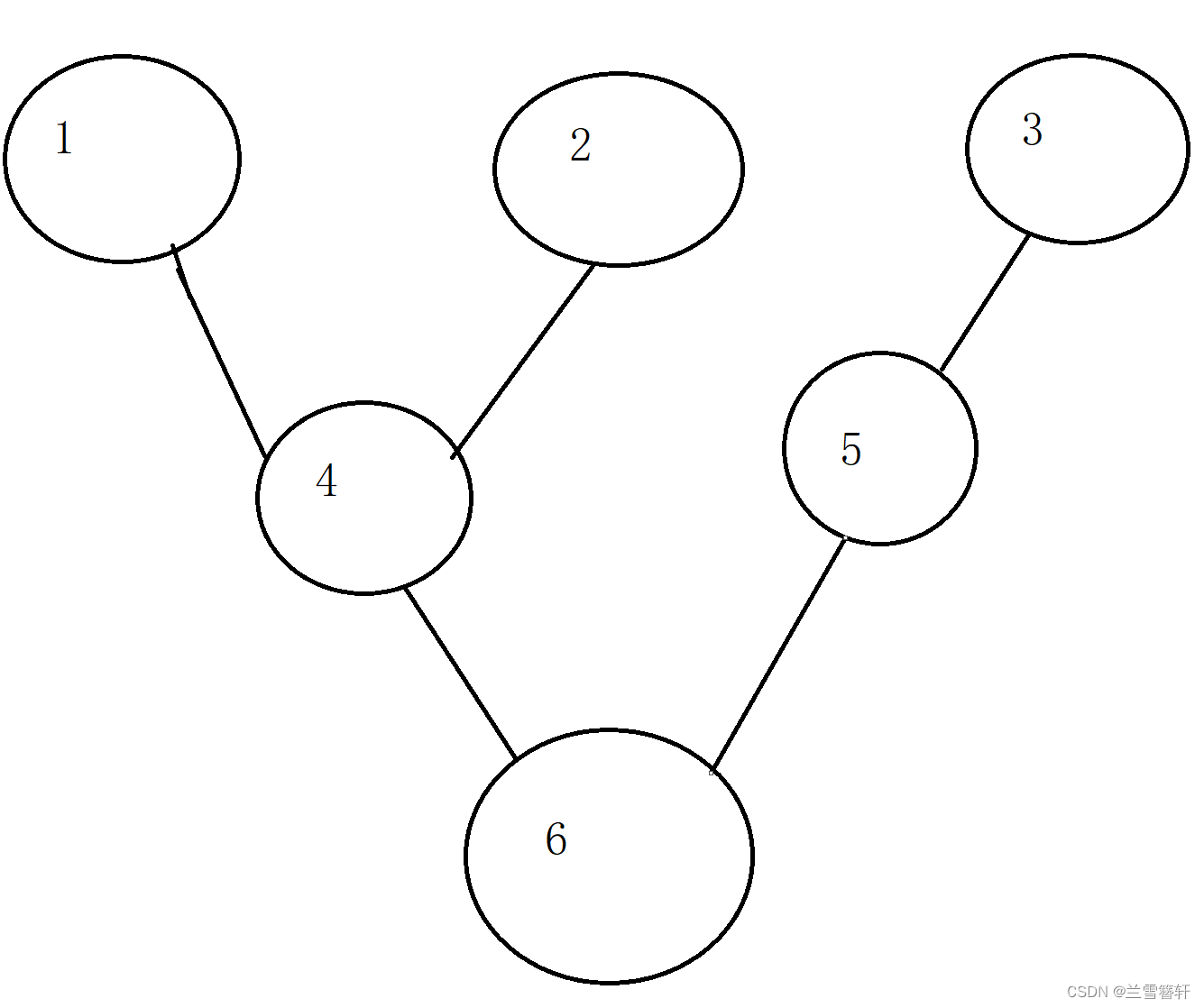
大家心目中的是图一还是图二呢?答案为图一。(选择图二的主要原因是本博主图画的丑,不是你们原因)。这时估计有人说了:不是说和树相似吗?我觉得图二明明比图一更相似,为什么不是图二。确实,图二的确更相似。但,你要明白,这样做肯定有人家这样做的道理。在后续对其实现中,你应该能体会到图一才能实现,图二这种只能在理论上实现。
好了,说了这么多,我来给大家介绍以下其基本的概念吧!吧毕竟是人家的主场。此处,节点与结点无任何本质区别,只有输入法的区别。 以以下这副图为例:
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、H、I等节点为叶节点
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m棵互不相交的树的集合称为森林;
以上,重要的概念已被加粗。
相信大家对于大部分概念都能够理解。接下来,我来简单解释一下为什么层次(高度)从一开始,不从零开始。
或许有人受数组影响,高度应该从零开始,不应该从一开始。假如你也这样想,你不妨这样想:如果树只有一个节点,那它的高度为0,那么,树要是没有节点,那它的高度为-1,是不是听着怪怪的。所以,我们规定:树的高度从一开始。
以上的概念,也没有必要强行记忆。各位可在后续实践和学习中遇到问题再来回顾即可。
二、树的性质
学习完概念后,我们就该明白其性质。学习完性质,可以使我们更好的理解树。大家可想一想,树的性质都围绕哪些特点展开?都包含哪一些?树的性质无外乎就围绕:节点和高度展开。以下是基本性质:
1)树中的结点数等于所有结点的度数之和加1。
2)度为m 的树中第i层上至多有m^(i-1)个结点(i≥1)。
3)高度为h的m叉树至多有(m^k-1)/(m-1)个结点,此处k = h。
4)具有n个结点的m叉树的最小高度为[ logm(n(m - 1)+1)。
5) 具有n个结点的树的最大高度h为n-m+1。
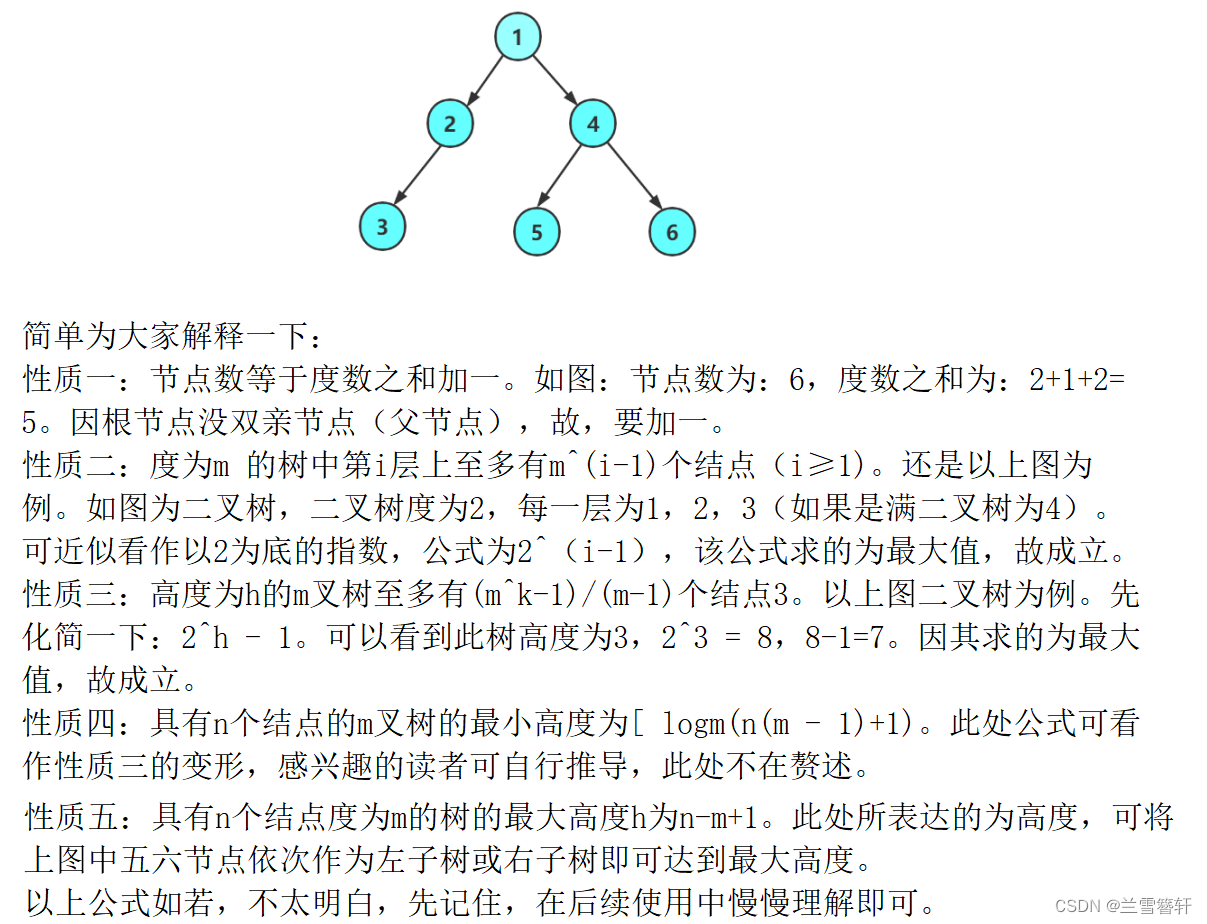
了解了性质后,来一道例题小试牛刀吧!
例题:
在一棵度为4的树T中,若有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T的叶结点个数是()。
A. 41 B.82 C.113 D.122
先公布答案吧,此题答案为B 82个叶节点。解析如下: 
三、二叉树
学习完树的概念,接下来,咱们一起来学习一下二叉树吧。
什么是二叉树呢?在学习完前面树的概念我们可以猜出来:二叉树即度为2的树称之为二叉树。可参考一下图片:
作为程序员的你和女朋友一起爬山时见到上面这颗树,当你女朋友惊叹于大自然的鬼斧神工时,你不和事宜飙出一句:wc,居然是满二叉树。你不由自主拜了一拜希望今后写的代码少些bug。只留下你女朋友在风中凌乱。(这个女朋友可能是广大读者杜撰出来的[doge])。
看到以上图片和文字,我们不禁要问:什么是满二叉树?别急,马上来问你解答疑惑。
我们学习二叉树,肯定会经历各种各样的树,以下涵盖了各个品种的树:
1)满二叉树。一棵高度为h,且含有2-1个结点的二叉树称为满二叉树,即树中的每层都含有最多的结点,满二叉树的叶结点都集中在二叉树的最下一层,并且除叶结点之外的每个结点度数均为 2。
可以对满二叉树按层序编号:约定编号从根结点(根结点编号为1)起,自上而下,自左向右。这样,每个结点对应一个编号,对于编号为i的结点,若有双亲,则其双亲为Li/2」若有左孩子,则左孩子为 2i;若有右孩子,则右孩子为 2i+1。
2)完全二叉树。高度为h、有n个结点的二叉树,当且仅当其每个结点都与高度为h的满二叉树中编号为 1~n 的结点一一对应时,称为完全二叉树其特点如下:
1.若 i≤(n/2),则结点i为分支结点,否则为叶结点。
2.叶结点只可能在层次最大的两层上出现。对于最大层次中的叶结点,都依次排列在该层最左边的位置上。
3.若有度为1的结点,则只可能有一个,且该结点只有左孩子而无右孩子(重要特征)。按层序编号后,一旦出现某结点(编号为i)为叶结点或只有左孩子,则编号大于的结点均为叶结点。
4.若n为奇数,则每个分支结点都有左孩子和右孩子;若n为偶数,则编号最大的分支结点(编号为n/2)只有左孩子,没有右孩子,其余分支结点左、右孩子都有。

3)二叉排序树。左子树上所有结点的关键字均小于根结点的关键字;右子树上的所有结点的关键字均大于根结点的关键字;左子树和右子树又各是一棵二叉排序树。
4)平衡二叉树。树上任意一个结点的左子树和右子树的深度之差不超过1。
咱们目前对于二叉树研究的重点为前两个。
既然明白其种类,那么也应该明白其性质,性质如下:
1)非空二叉树上的叶结点数等于度为2的结点数加1,即no=n2+1。(此性质在选择题中常用,拓展到任意一棵树,若结点数量为 n,则边的数量为n-1。)
2)非空二叉树上第k层上至多有2^(k-1)个结点(k>1)。3)高度为h的二叉树至多有 2"-1个结点(h>1)。
4)对完全二叉树按从上到下、从左到右的顺序依次编号1,2,…,n,则有以下关系:
1.当i>1时,结点i的双亲的编号为(i/2),即当i为偶数时,其双亲的编号为i/2,它是双亲的左孩子;当i为奇数时,其双亲的编号为(i-1)/2,它是双亲的右孩子。
2.当 2i≤n时,结点i的左孩子编号为2i,否则无左孩子
当 2i+1≤n时,结点i的右孩子编号为2i+1,否则无右孩子。3.结点i所在层次(深度)为(logi)+1。
5)具有n个(n>0)结点的完全二叉树的高度为[log(n+1)]或 [logn]+ 1。
这里的性质就不过多解释,大部分处于树性质的变形。
来道例题巩固一下吧:
若一棵完全二叉树有 768个结点,则该二又树中叶结点的个数是( )。
A.257 B.258 C.384 D385
答案为: C。解析如下:
四、堆
这里简单介绍一下二叉树的一种结构堆。(注:在现阶段二叉树中只学习堆与二叉树(部分)的实现,以及OJ题,以后的内容会在C++学习,本篇文章,只是先使读者明白概念,其具体实现方式以及讲解会在后续文章中发出,还望理解。)
说起堆,相信大部分读者会想起把柴火或其他物品堆起来的画面,我们发现,其结构似乎与二叉树类似,都有点头重脚轻的。对的,在数据结构中,堆的本质为:完全二叉树。
堆有一下性质:
堆中每个节点的值都满足堆的性质:堆中某个节点的值总是不大于或不小于其父节点的值。
大跟堆(Max Heap),父节点的值大于等于其子节点的值。
小根堆(Min Heap),父节点的值小于等于其子节点的值。
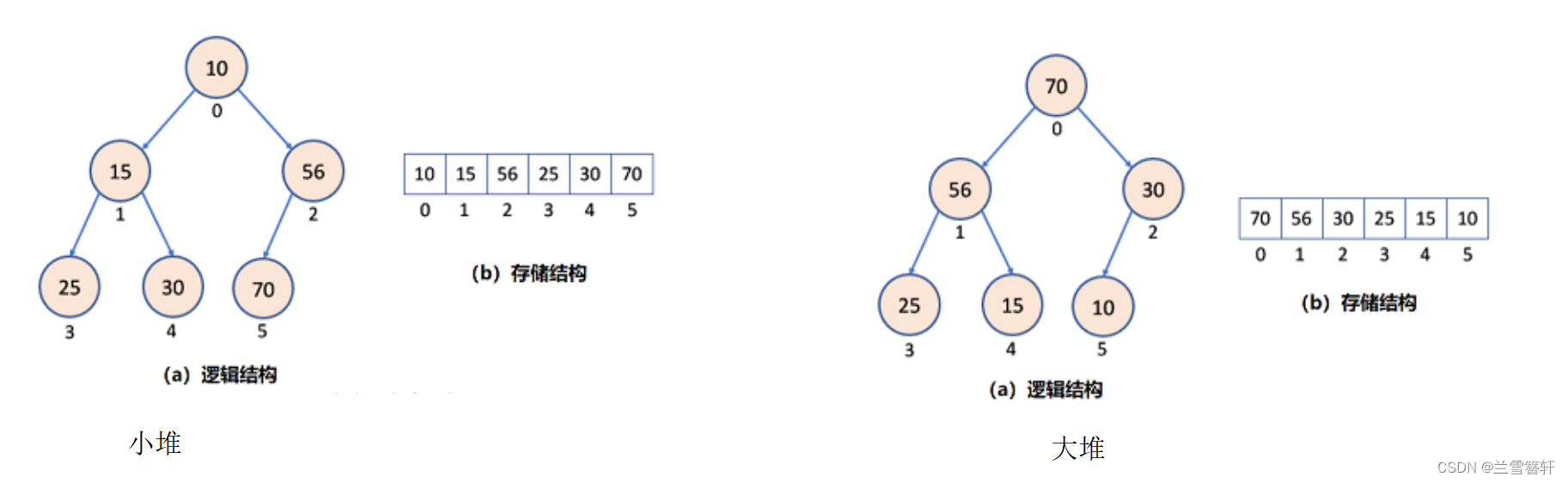
明白了基本概念,来一道例题吧:
1.下列关键字序列为堆的是:
A 100,60,70,50,32,65B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
此题答案为A。做堆的题,画图为最优解。解析如下: 
最后
对于二叉树基础的理论知识,我们就学习到这里,虽然这些知识相对后面来说简单一点,但别忘记复习。有了这些预备知识才能够更好的理解后面知识。另外对于递归理解还不够的读者一定要去尽可能的去理解,对于二叉树的学习非常重要。今天的学习就结束了,有问题可在评论区交流,也可私信。我们下篇见!
二叉树对堆的深入理解:CSDN
对二叉树的深入理解:CSDN
完!