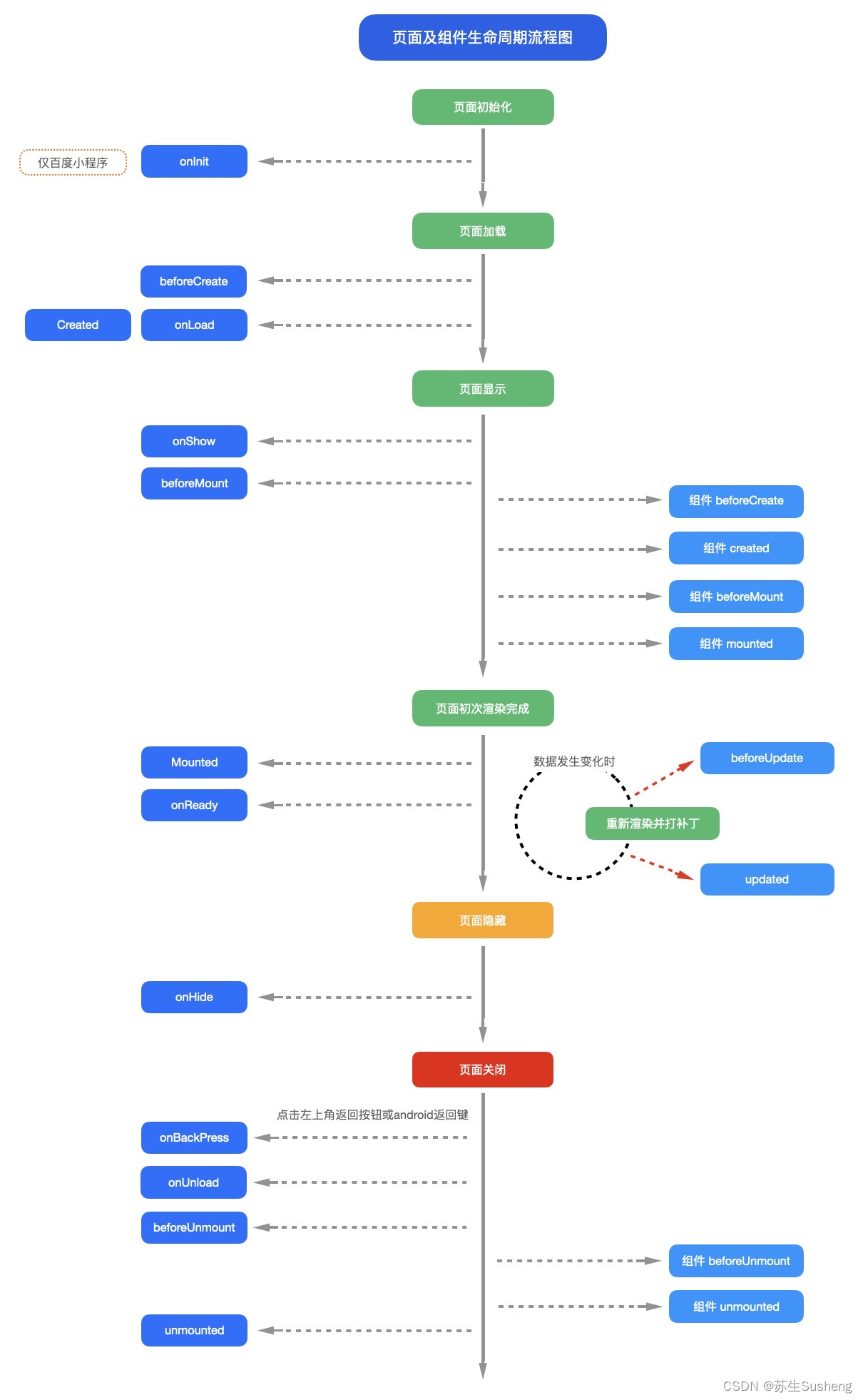
树

树是一种非线性的数据结构
树是根朝上的，叶子是朝下的
树是递归定义的【根+N棵子树】
递归定义：大事化小，可以理解为套娃

树的子树之间是独立的，所以子树之间是不相交的
如果子树之间相交那么这将称为图

树的概念

这里就介绍比较重要的
树的关系可以看做是亲缘关系

度：就是一个节点含有的子树的个数称为该节点的度
比如A节点含有6个子树，度是6
度为0的叫叶子节点 B C H I P Q
度不为0的叫分支节点 D E F G J

叶节点：叶节点是没有子树的节点，也是度为0的节点
比如上图中的 P Q

双亲节点或父节点：若一个节点含有子节点，则称这个节点是它子节点的父节点
例如：A是B的父节点

子节点或孩子节点：一个节点含有的子树的根节点，父亲节点的下一个节点是孩子节点
例如：B是A的孩子节点

树的高度或深度：树中节点的最大层次
有两种表示方法：
1.只有根节点表示1层
空树表示0层
2.只有根节点表示0层
空树表示-1层
虽然两种都可以，但是第一种表示方法更好

树是递归定义的【根+N棵子树】
递归定义：大事化小，可以理解为套娃

例如：A树下面有B C D三棵子树，B C D下面又有子树

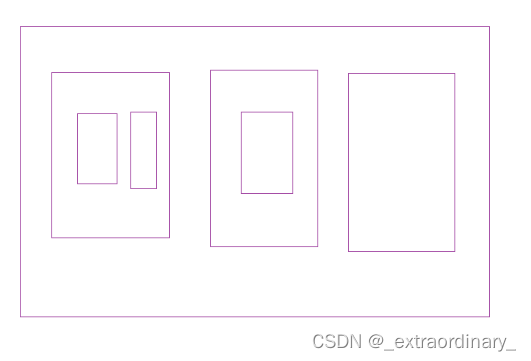
完全二叉树和满二叉树

满二叉树是特殊的二叉树
满二叉树是特殊的完全二叉树
是满二叉树一定是完全二叉树
是完全二叉树不一定是满二叉树

满二叉树：
1.从上到下都是满的，从左到右节点都是连续的

完全二叉树：
1.到h-1层都是满节点的，最后1层是不满的，但是从左到右必须是连续的
2.从左到右中间有空就不是完全二叉树

例如：满二叉树的时间复杂度：O(logN)
找一个节点会找高度次

完全二叉树存储

完全二叉树可以用数组存储，也可以用链表存储

完全二叉树用数组存储

用数组存储：
逻辑结构：是想象出来的，是完全二叉树
物理结构：是内存中实实在在存储的

假设父亲的下标是：i
左孩子的下标：2i + 1
右孩子的下标：2i + 2

假设孩子的下标是：j
父亲的下表是：(j-1) / 2

非完全二叉树可以用数组存储吗？
答案是可以的，但是有很多空间的浪费

堆

栈和堆是一种数据结构

在C语言中也有栈和堆，那它们也是数据结构吗？
答案不是的，C语言中的栈和堆是操作系统中的可以存储数据的空间
比如局部变量就存在于栈上，malloc，动态开辟的空间存储在堆上，数组也存储在堆上

在数据结构中堆也是二叉树的一种
堆又分为小堆和大堆

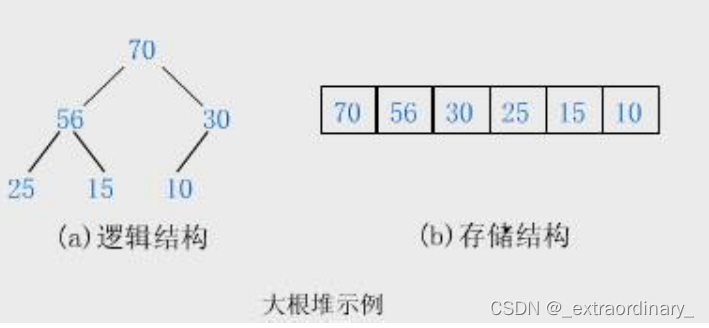
大堆：
1.父亲节点大于任何一个它的孩子节点（根是最大的）
2.必须是完全二叉树

小堆：
1.父亲节点小于任何一个它的孩子节点（根是最小的）
2.必须是完全二叉树