题目链接
问题描述
答案提交
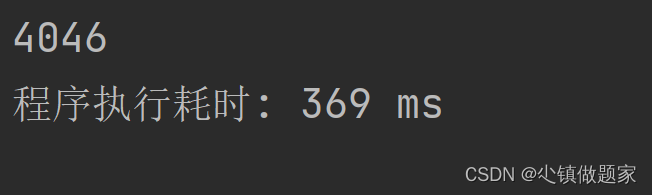
本题答案是:4046。
运行限制
思路分析
代码(Java)
问题描述
小蓝国是一个水上王国, 有 2021 个城邦, 依次编号 1 到 2021。在任意两 个城邦之间, 都有一座桥直接连接。
为了庆祝小蓝国的传统节日, 小蓝国政府准备将一部分桥装饰起来。
对于编号为 a 和 b 的两个城邦, 它们之间的桥如果要装饰起来, 需要的费 用如下计算:
找到 a 和 b 在十进制下所有不同的数位, 将数位上的数字求和。
例如, 编号为 2021 和 922 两个城邦之间, 千位、百位和个位都不同, 将这些数位上的数字加起来是 (2+0+1)+(0+9+2)=14 。注意 922 没有千位, 千位看成 0 。
为了节约开支, 小蓝国政府准备只装饰 2020 座桥, 并且要保证从任意一个 城邦到任意另一个城邦之间可以完全只通过装饰的桥到达。
请问, 小蓝国政府至少要花多少费用才能完成装饰。
提示: 建议使用计算机编程解决问题。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
本题答案是:4046。
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
思路分析
首先,他的花费计算是,两个数A,B,如果A和B相对应的位数不同,就相加。
如:2017和917这两个数的花费是:(2+0)+(0+9),因为个位他们都是7,所以省略了,十位也是同理,然后917没有千位,默认是0。所以2017和917的花费就是(2+0)+(0+9)=11
然后再看题目,很明显跟图有关,一共有2021个节点,题目要求我们让所有节点都能连通起来,让我们使用2020条边,同时要求花费最少。
判断是否连通需要用到并查集,然后在确保花费最少可以用贪心的策略,每次选择花费最少的一条边,让两个节点相连。
条件这么清楚了,很明显的要用到最小生成树了,这道题就是经典板子题。
如果不了解什么是最小生成树,可以搭配视频理解,我下面简单说一下。
视频链接:最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示
首先,需要是一个带权的图,在本题中,两个城堡之间如果需要连接起来,那么需要花费一定费用,将两座城堡之间建立连接。那么,换个思路来,两个城堡是图中的节点,然后他们之间互相连接的边,就是这两座城邦建立连接所需要的花费;而且,我们需要任意一个城堡都能到达另一个城堡,那么,就代表着这些节点之间需要互相连通,这样他们才能互相到达另一边。
因此可以把题目的城堡当作连通带权无向图来处理。
题目条件也给出了,一共有2021个城堡,也就是一共有2021个节点。我们需要用2020座桥把他们连接起来,也就是一共有2020条边。并且我们要让花费最小。
所谓的最小成本了:就是n个顶点,用n-1条边把一个连通图连接起来,并使得权值的和最小。所以,我们把构成连通图的最小代价生成树叫做最小生成树。
而最小生成树,有两个经典的算法,Kruskal和Prim,这里我们使用Kruskal比较容易理解。
我们可以将节点x与节点y的花费存起来,用一个类(结构体)来存储节点x,节点y,节点x与y的连通花费。
class Node{
// x <-> y
int x; //节点x
int y; //节点y
int cost; //连接x和y的花费
public Node(int x, int y, int cost) {
this.x = x;
this.y = y;
this.cost = cost;
}
}然后将其存入一个数组之中,之后遍历1-2021,算出所有节点互相之间连通需要的花费,并存入数组之中,后续按照连通花费,进行升序排序,这样保证前面的连通花费是最少的,我们根据Kruskal的思想,从最少连通花费进行连接,把x和y连接起来。
将1-2021之间所有节点与边的关系添加到数组之后,我们就需要对数组进行排序了,要完成Kruskal算法之中花费从小到大排序,也就是升序,我们就需要对数组进行排序。
但是我们开的数组肯定是远大于我们实际需要使用到的大小,所以我们需要用一个变量记录使用到哪个位置,然后排序的时候选择从0-变量记录的位置,然后使用升序排序即可(一般默认排序都是升序排序)。之后就是判断连通的问题了。
既然要判断是否连通,那么就要用到并查集来检查连通了。
如果对并查集不太懂,可以看:【算法与数据结构】—— 并查集 (写的非常好)。
这里贴上代码,不展开介绍了。
int[] pre;
public void initPre(){
//并查集找连通
pre = new int[2022];
//初始化并查集
for(int i = 0;i<pre.length;i++){
pre[i] = i;
}
}
public int find(int x){
//做一下路径压缩
if(pre[x] == x) return x;
return pre[x] = find(pre[x]);
}
public void join(int x,int y){
int fx = find(x);
int fy = find(y);
if(fx!=fy)
pre[fx] = fy;
}如果将x和y连通,将产生环,该如何判断呢?
我们需要通过并查集找到节点x它的父亲是谁,和y的父亲进行比较,如果他们的父亲相同,代码x已经可以和y同时到达同一个地点,如果我们再让x和y进行连接,那么肯定会产生环。
如: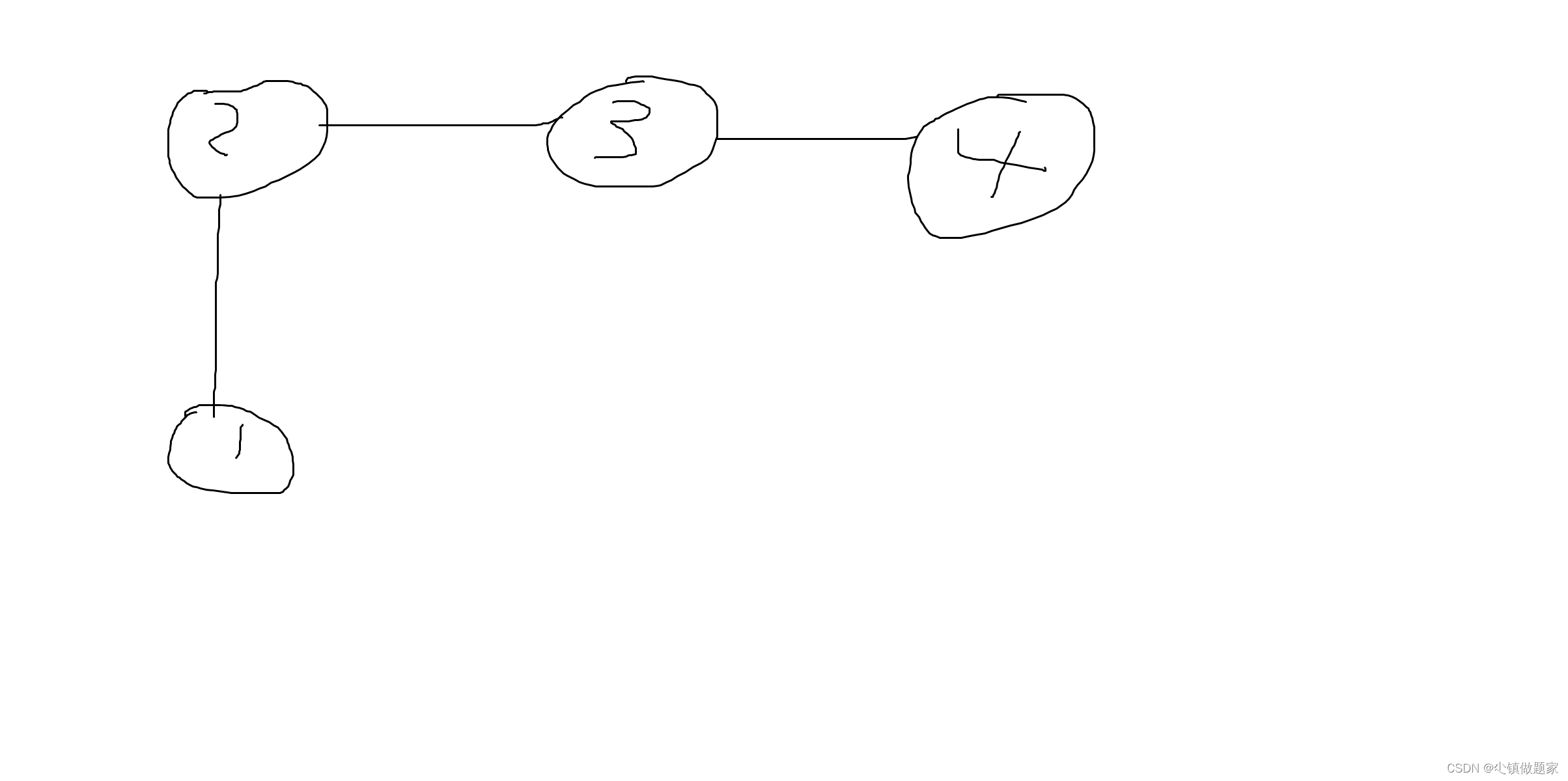
如果我们的x是1,y是3,我们通过并查集的find()可以知道他们的父亲都是4,如果再让他们连通,则肯定会产生环。
所以我们需要判断x和y的父亲是不是同一个,如果不是,那么就可以使用并查集的join()将他们连接起来,并且将连接他们的花费记录到答案之中,因为这是构造连通的最优解。
之后根据定义,我们只需要成功连通2020个边(n个节点需要n-1个边),就完成了1-2021之间的连通,他们之间就可以从任意一个节点到另一个节点,并且花费是最小的了。
代码(Java)
不知道为什么在蓝桥那边提交显示超时,我在本地跑就只用了380±20ms。
import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
static int[] pre;
public static int find(int x){
//做一下路径压缩
if(pre[x] == x) return x;
return pre[x] = find(pre[x]);
}
public static void join(int x,int y){
int fx = find(x);
int fy = find(y);
if(fx!=fy)
pre[fx] = fy;
}
static class Node{
// x <-> y
int x; //节点x
int y; //节点y
int cost; //连接x和y的花费
public Node(int x, int y, int cost) {
this.x = x;
this.y = y;
this.cost = cost;
}
}
public static void main(String[] args) {
//程序开始时间
long startTime = System.currentTimeMillis();
//并查集找连通
pre = new int[2022];
//初始化并查集
for(int i = 0;i<pre.length;i++){
pre[i] = i;
}
//空间换时间
Node[] minTree = new Node[2021*2021];
int index = 0;
//将边的信息存储到数组中
for(int i = 1;i<2021;i++){
for(int j = i+1;j<=2021;j++){
int cost = cost(i,j);
minTree[index++] = new Node(i,j,cost);
}
}
//按照花费进行升序排序,排序范围是0-index,也就是存储有边信息的部分
Arrays.sort(minTree,0,index,(n1,n2)->(n1.cost-n2.cost));
//总花费
int res = 0;
//依次取出顶部(前面)的边,判断该x和y添加进去是否会产生环,如果不会就使用这条边;如果会就丢弃这条边
for(int i = 0;i<index;i++){
Node node = minTree[i];
if(find(node.x)!=find(node.y)){
join(node.x,node.y);
res += node.cost;
}
}
System.out.println(res);
//程序结束时间
long endTime = System.currentTimeMillis();
System.out.println("程序执行耗时: "+(endTime-startTime)+" ms");
}
public static int cost(int x,int y){
int res = 0;
while(x>0 || y>0){
int a = x%10;
int b = y%10;
if(a!=b) res += a+b;
x /= 10;
y /= 10;
}
return res;
}
}程序运行结果:

![[Linux]进程概念以及进程状态](https://img-blog.csdnimg.cn/344e7b45e32f4042ab62a76d42887351.png)