目录
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
二、解题报告
1、思路分析
2、复杂度
3、代码详解
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
0打折 - 蓝桥云课 (lanqiao.cn)
二、解题报告
1、思路分析
思路很简单,按照时间顺序遍历,计算该天购买所有商品的总价格然后维护最小值
我们考虑对于一件物品在[l, r]内打折,等价于在第l天开始打折,第r+1天结束打折
那么我们可以用结构体存储如下信息:第 i 天,商品a调整价格为b
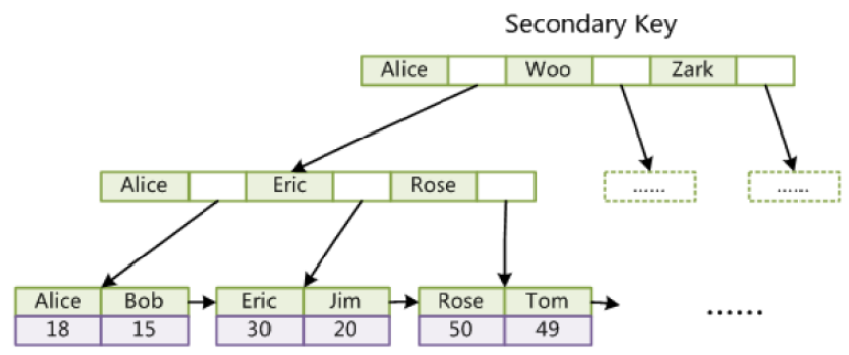
用平衡树维护每个商品当前有效价格集合
然后对于[l, r] 打折的商品<a, b>我们存两个结构体
第l天,商品a调整价格为b * p * / 100
第r + 1天,商品a 调整价格为 -1 - b * p * / 100
第一个很好理解,第二个并非是真的这样,而是我们遍历到该信息后得知商品a之前的价格没用了,我们用-1减去结构体内的价格就能得到之前的价格,我们从商品a的价格集合中删去即可
读入信息后,将结构体按时间升序排序,顺序遍历,每次处理一天内的所有信息
然后维护最小值即可
注意multiset如果erase(key)会将key都删掉,如果是erase(st.find(key))只会删除一个
2、复杂度
时间复杂度: O(nlogn)空间复杂度:O(n)
3、代码详解
#include <bits/stdc++.h>
using i64 = long long;
using PII = std::pair<int, int>;
const int N = 1e5 + 10, M = 8e5 + 10;
int n, m, tot;
struct node {
int s, w, id;
bool operator < (const node& x) const {
return s < x.s;
}
} q[M];
std::multiset<int> st[N];
int main () {
std::cin >> n >> m;
std::vector<int> w(n + 1, 1e9);
for (int i = 0, s, t, p, c; i < m; i ++ ) {
std::cin >> s >> t >> p >> c;
for (int j = 0, a, b; j < c; j ++ ) {
std::cin >> a >> b;
w[a] = std::min(w[a], b);
int x = 1LL * b * p / 100;
q[tot ++] = { s, x, a };
q[tot ++] = { t + 1, -x - 1, a };
}
}
for (int i = 1; i <= n; i ++ ) st[i].insert(w[i]);
std::sort(q, q + tot);
i64 ans = std::accumulate(w.begin() + 1, w.end(), 0LL);
i64 s = ans;
for (int i = 0; i < tot; ) {
int t = q[i].s;
while (i < tot && q[i].s == t) {
s -= *st[q[i].id].begin();
if (q[i].w < 0)
st[q[i].id].erase(st[q[i].id].find(-1 - q[i].w));
else
st[q[i].id].insert(q[i].w);
s += *st[q[i].id].begin();
i ++;
}
ans = std::min(ans, s);
}
std::cout << ans;
return 0;
}








![[Android]将私钥(.pk8)和公钥证书(.pem/.crt)合并成一个PKCS#12格式的密钥库文件](https://img-blog.csdnimg.cn/direct/254530f1f33f4653ba488c11ae8a58aa.png)