目录
机器学习实践
机器学习基础理论和概念
机器学习基本方法
1.线性回归(回归算法)
训练集(Training Set)
测试集(Test Set)
交叉验证
正则化
特点
2.logistic回归(分类算法)
特点
3.决策树
ID3与C4.5算法
梯度提升
GBDT模型与xgboost
决策树总结
4.朴素贝叶斯算法(文本分类模型)
贝叶斯公式
语言模型
马尔科夫假设
特点
机器学习实践
机器学习基础理论和概念
机器学习主要是研究如何使计算机从给定数据中学习规律,并利用学习到的规律(模型)来对未知或无法观测的数据进行预测。
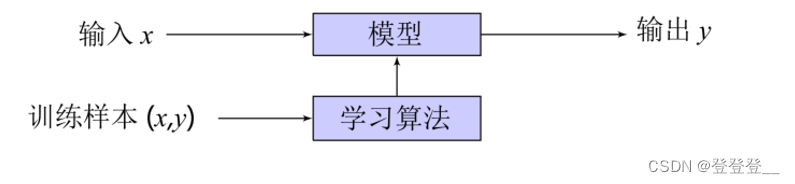

机器学习基本方法
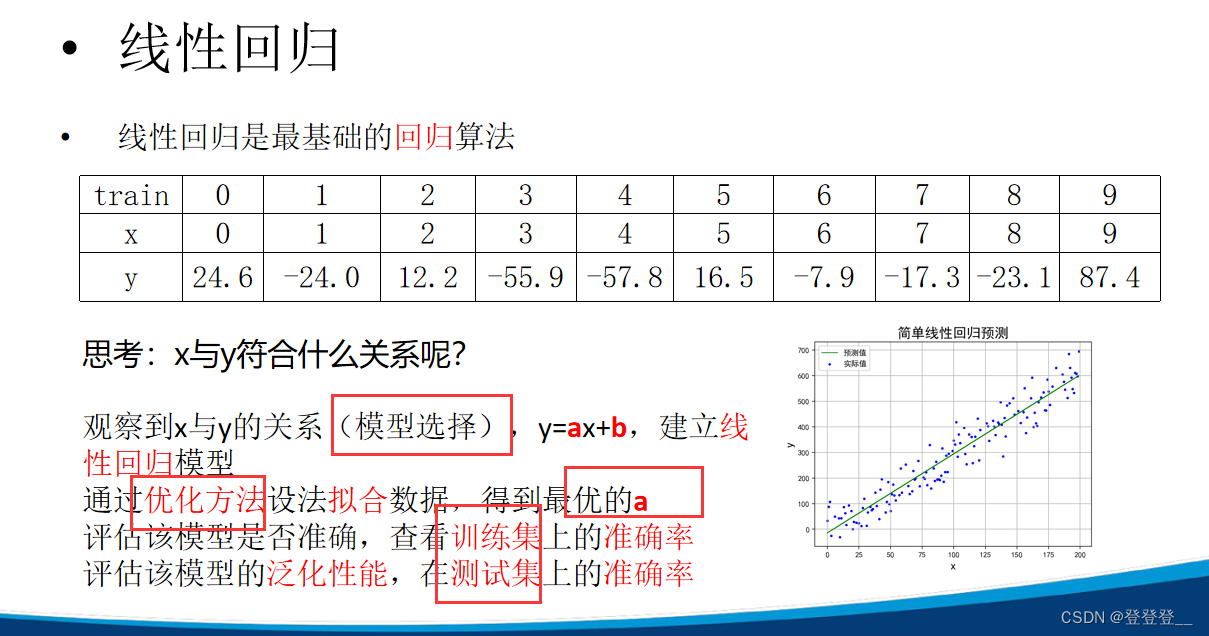
1.线性回归(回归算法)
线性回归(Linear Regression)是一种统计学上分析变量之间关系的预测模型,它试图建立一个因变量(目标变量)与一个或多个自变量(特征变量)之间的线性关系。这种关系的形式是通过拟合一个最佳直线(在只有一个自变量时)或超平面(在有多个自变量时)来建立的,使得预测值与实际观测值之间的残差平方和最小。
线性回归模型的基本形式为:
(Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_pX_p + \epsilon)
其中:
- (Y) 是因变量(响应变量)。
- (X_1, X_2, \ldots, X_p) 是自变量(预测变量或特征)。
- (\beta_0, \beta_1, \ldots, \beta_p) 是回归系数,其中 (\beta_0) 是截距,(\beta_1, \ldots, \beta_p) 是斜率。
- (\epsilon) 是误差项,表示模型未能解释的变异。
线性回归的主要目的是估计回归系数 (\beta_0, \beta_1, \ldots, \beta_p),这通常通过最小二乘法来实现,即最小化残差平方和。一旦得到了这些系数的估计值,模型就可以用来预测新的观测值的因变量值。
线性回归在数据分析、机器学习、经济学、社会科学和自然科学等领域都有广泛的应用。它可以帮助人们理解变量之间的关系,进行预测和推断,并作出基于数据的决策。然而,值得注意的是,线性回归模型假设因变量和自变量之间存在线性关系,并且误差项满足一定的条件(如正态性、独立性和同方差性)。在实际应用中,需要检验这些假设是否成立,并根据具体情况对模型进行调整或选择其他更合适的模型。
在机器学习,特别是线性回归中,我们通常将数据集分为训练集(Training Set)和测试集(Test Set)以评估模型的性能。这种划分有助于我们了解模型在未见过的数据上的表现。
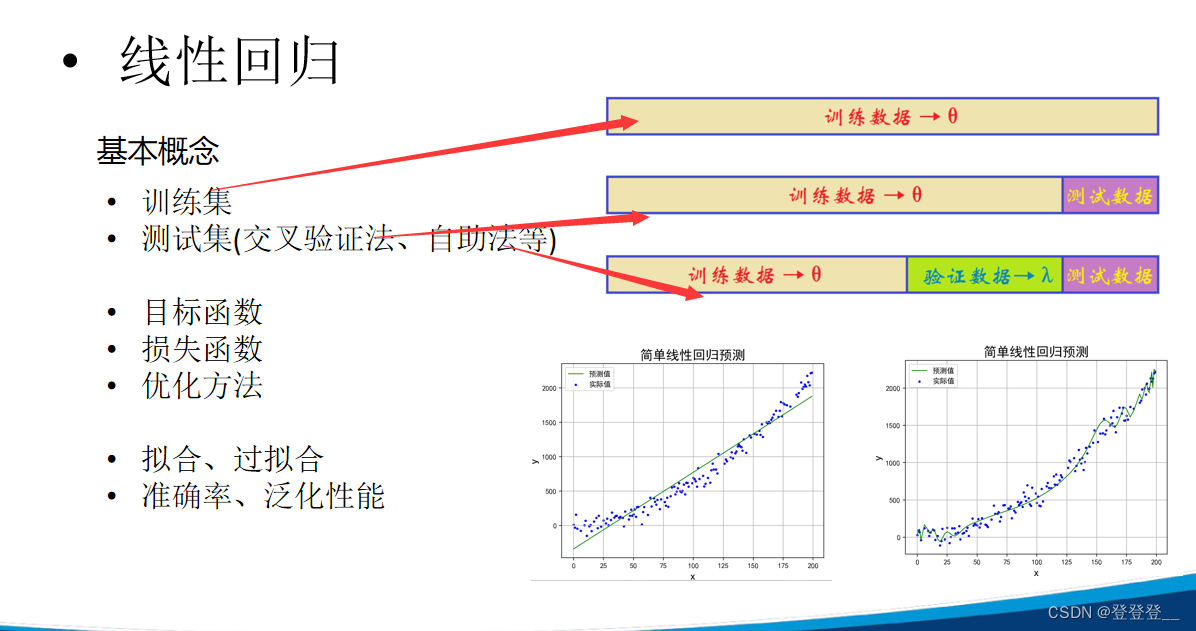
训练集(Training Set)
训练集用于训练模型,即确定线性回归模型的参数(斜率和截距)。在训练过程中,模型会尝试找到最佳拟合训练数据的参数,以最小化预测误差。
测试集(Test Set)
测试集用于评估训练好的模型的性能。它包含模型在训练过程中未见过的数据。通过将模型应用于测试集,我们可以得到模型在未知数据上的预测结果,并与实际结果进行比较,从而计算模型的性能指标(如均方误差MSE、R平方值等)。
为什么要划分训练集和测试集?
- 防止过拟合:如果只使用整个数据集进行训练和评估,模型可能会过度拟合训练数据,导致在未见过的数据上表现不佳。通过划分训练集和测试集,我们可以确保模型在未见过的数据上进行评估,从而更准确地评估其性能。
- 模型选择:在多个候选模型中选择最佳模型时,我们可以使用训练集进行训练,并使用测试集的性能指标进行比较。这样可以确保我们选择的模型不仅在训练数据上表现良好,而且在未见过的数据上也具有良好的泛化能力。
如何划分?
通常,训练集和测试集的划分比例可以是70%-30%、80%-20%等,具体取决于数据集的大小和问题的复杂性。在某些情况下,还可以使用交叉验证(Cross-Validation)等技术来进一步评估模型的性能。
总之,通过合理划分训练集和测试集,我们可以更好地训练和评估线性回归模型,从而得到更准确、更可靠的预测结果。
交叉验证
交叉验证(Cross-Validation,简称CV)是一种统计学方法,主要用于评估机器学习模型的性能。它的主要目的是确保模型在新的、未见过的数据上也能表现得很好,从而避免过拟合。
在交叉验证中,数据通常被分为训练集和测试集(有时还包括验证集)。模型在训练集上进行训练,并在测试集上进行评估。通过多次评估模型的性能,交叉验证提供了对模型在未见过的数据上表现的更稳健的估计。
交叉验证有多种形式,其中较为常见的是k折交叉验证(如10折交叉验证)。在k折交叉验证中,数据集被分为k个子集。然后,轮流将k-1个子集用作训练数据,剩下的一个子集用作测试数据。这个过程重复k次,每次使用不同的子集作为测试数据。最后,对k次的结果进行平均,以得到一个对模型性能的总体估计。
通过交叉验证,我们可以得到可靠稳定的模型,特别是在数据量有限或模型选择和调整的情况下。这种方法在建模应用中,如PCR、PLS回归建模中,被广泛使用。
需要注意的是,虽然交叉验证是一种强大的工具,但它也有其局限性。例如,它可能会增加计算成本,特别是当数据集很大或模型很复杂时。因此,在实际应用中,需要根据具体情况权衡其利弊。





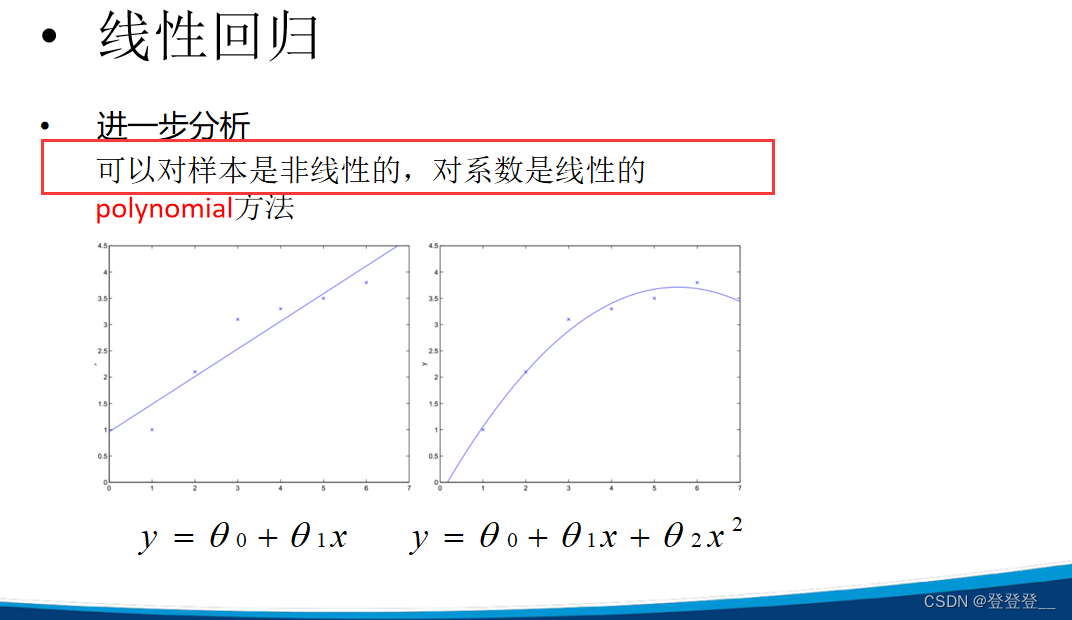

Precision与Accuracy(准确度)是不同的概念。Accuracy是描述每一次独立的测量之间,其平均值与已知的数据真值之间的差距,而Precision则更侧重于实验数据的一致性或再现性2。

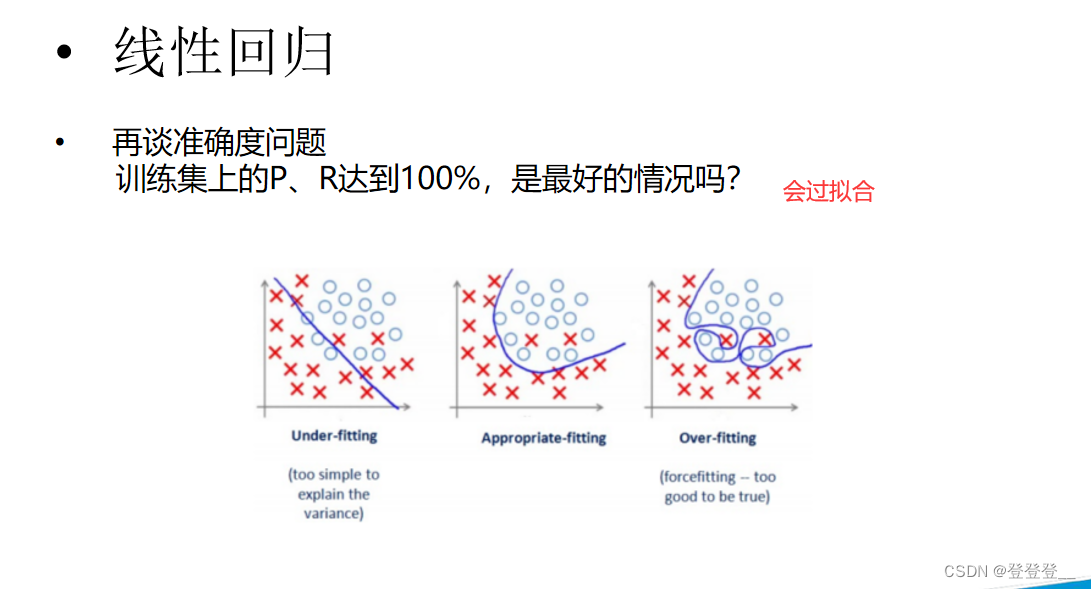
正则化

特点
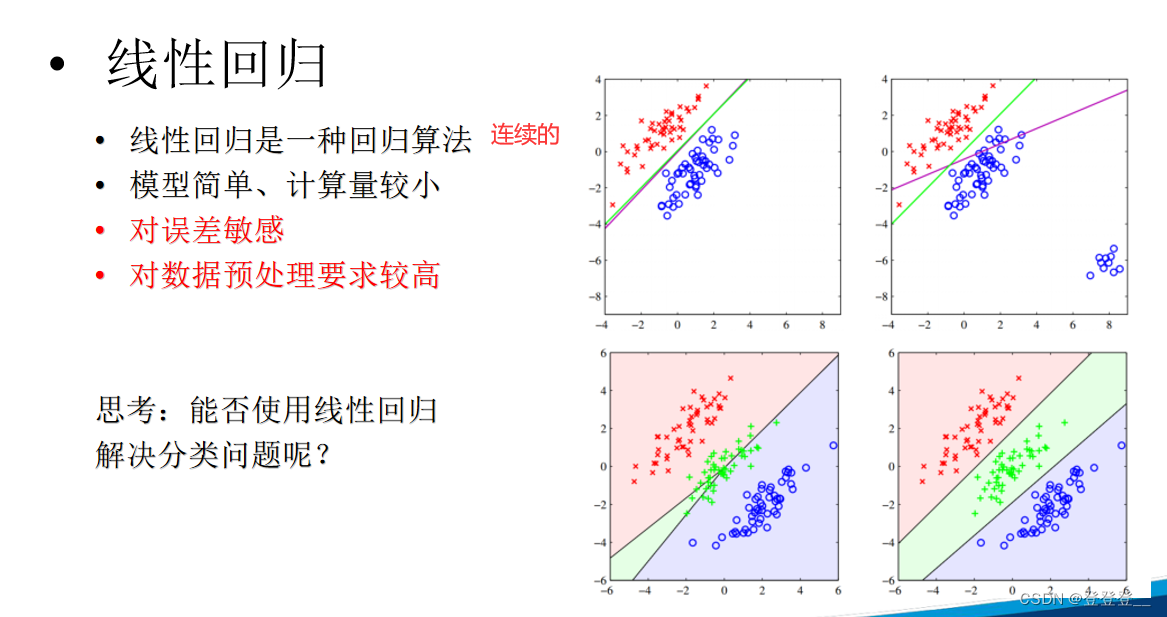
线性回归本身并不能直接用于解决分类问题。线性回归是一种基本的回归分析方法,主要用于探索自变量与因变量之间的线性关系,并预测连续型的因变量。其原理是通过拟合一条(或多条)直线(或平面)来最小化预测值和观测值之间的差异,从而得到最佳的截距和系数。
然而,通过对线性回归做出简单的变换,如逻辑斯蒂回归(logistic regression),可以用于解决二分类问题。逻辑斯蒂回归是在线性回归的基础上,通过应用一个逻辑函数(通常是sigmoid函数)将线性预测值转换为概率值,从而实现对分类问题的建模。对于多分类问题,可以通过将多分类问题分解成多个二分类问题来解决,进而应用逻辑斯蒂回归或其他多分类算法。
因此,虽然线性回归本身不直接适用于分类问题,但通过一些变换和扩展,可以间接地用于分类任务。但需要注意的是,选择适合问题特性的模型和算法至关重要,线性回归及其变换形式可能并不适用于所有类型的分类问题。在实际应用中,应根据问题的具体需求和数据的特性来选择合适的模型和方法。
2.logistic回归(分类算法)
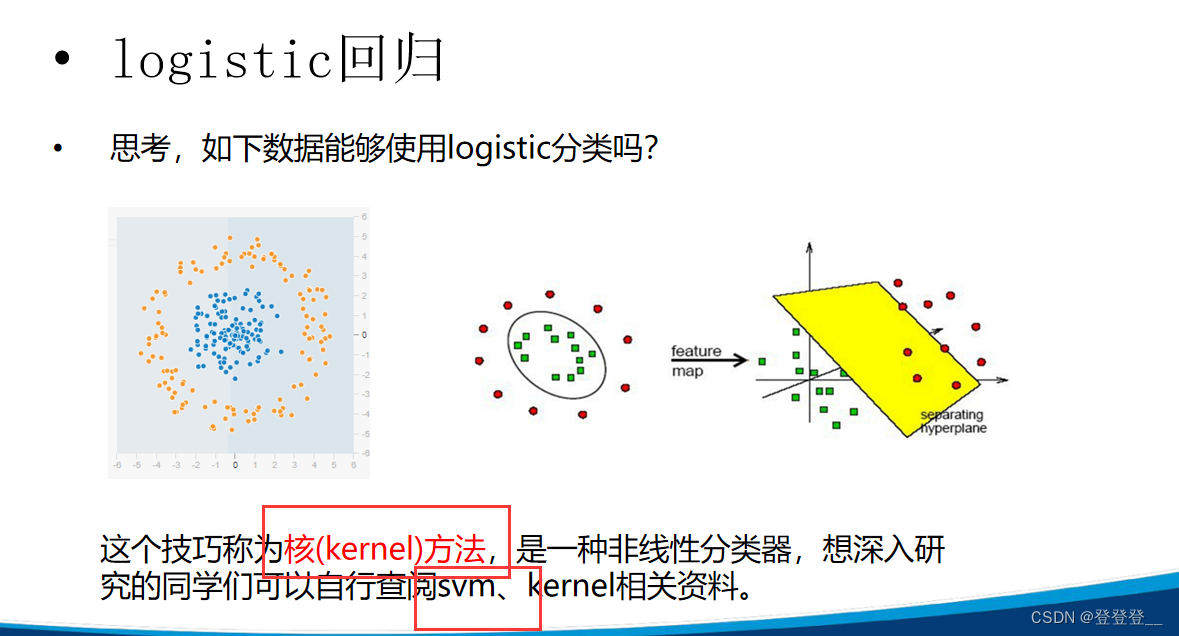
Logistic回归,又称为逻辑斯蒂回归分析,是一种广义的线性回归分析模型。它常用于数据挖掘、疾病自动诊断、经济预测等领域。Logistic回归根据给定的自变量数据集来估计事件的发生概率,由于结果是一个概率,因此因变量的范围在0和1之间。
在实际应用中,Logistic回归经常用于研究某些因素条件下某个结果是否发生。比如,在医学领域,可以根据病人的症状来判断其是否患有某种疾病。
Logistic回归可以分为二分类和多分类,其中二分类的Logistic回归更为常用且易于解释。对于多分类问题,可以使用softmax方法进行处理。





特点
3.决策树
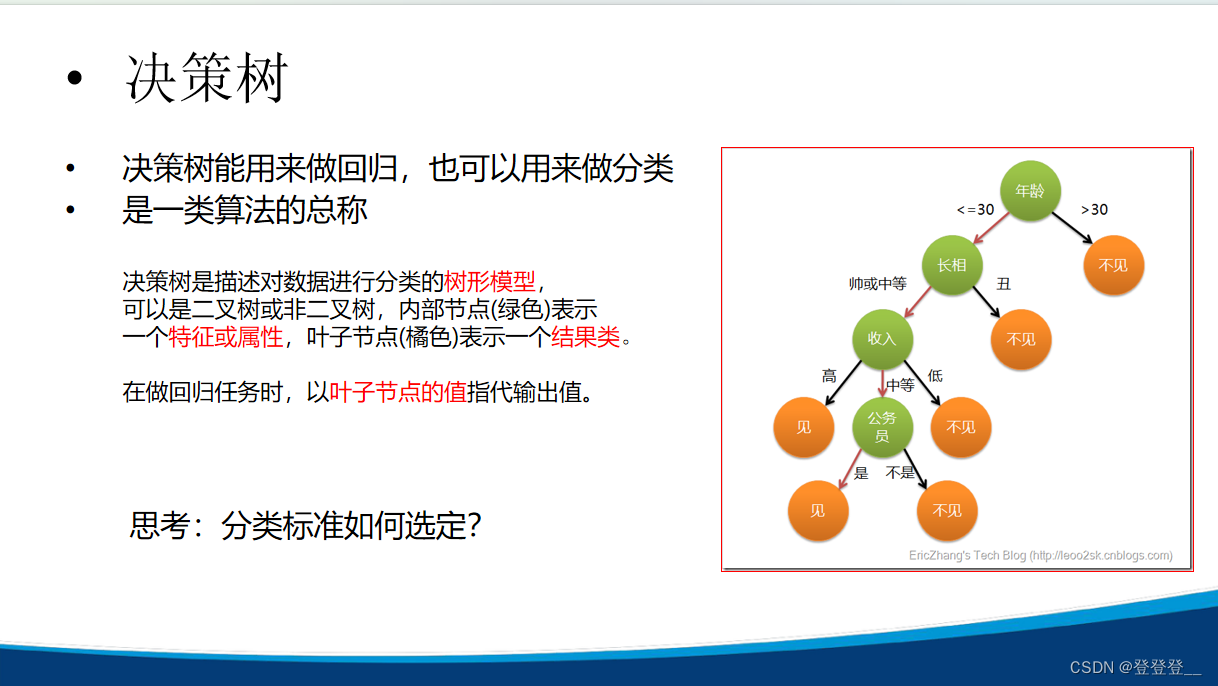
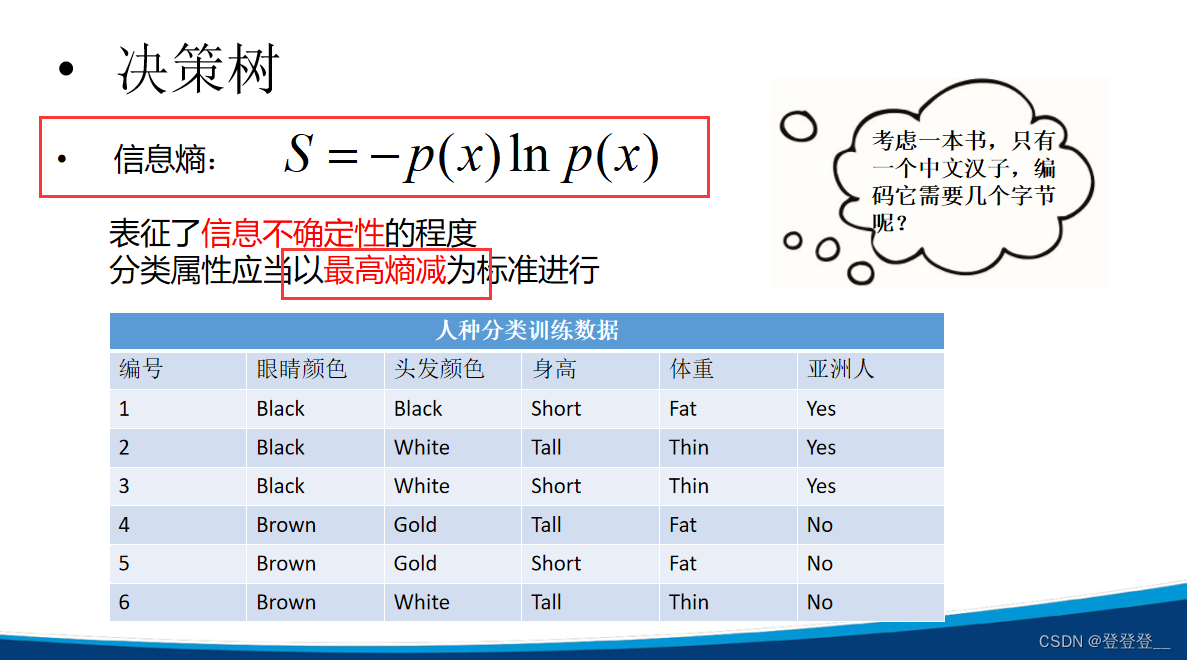

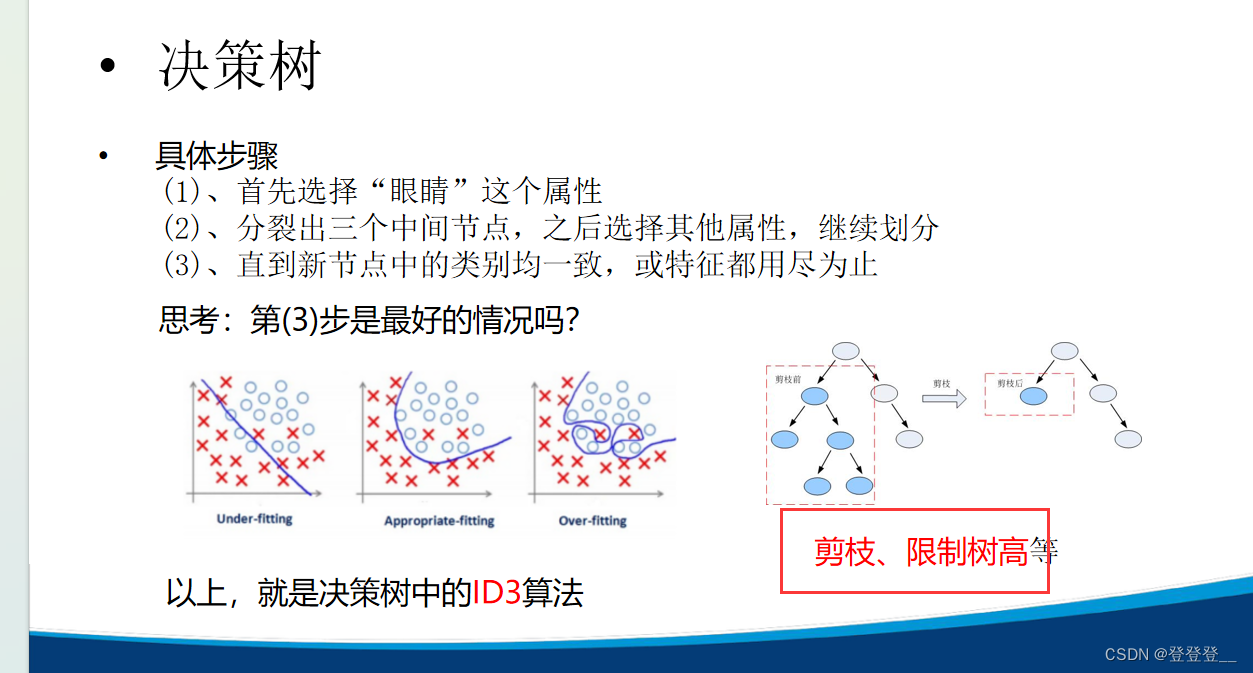
ID3与C4.5算法


梯度提升

GBDT模型与xgboost
CART是决策树的一种实现,它既可以用于分类问题,也可以用于回归问题。作为一种二分递归分割技术,CART算法通过递归地将数据集划分为两个子集来构建决策树,使得生成的每个非叶子结点都有两个分支,因此CART算法生成的决策树是结构简洁的二叉树。
XGBoost在Gradient Boosting框架下实现机器学习算法,提供并行树提升(也称为GBDT,GBM),可以快速准确地解决许多数据科学问题。其目标函数由梯度提升算法损失和正则化项两部分构成,损失函数中加入了正则化项以防止过拟合,并提高了模型的泛化能力。



决策树总结

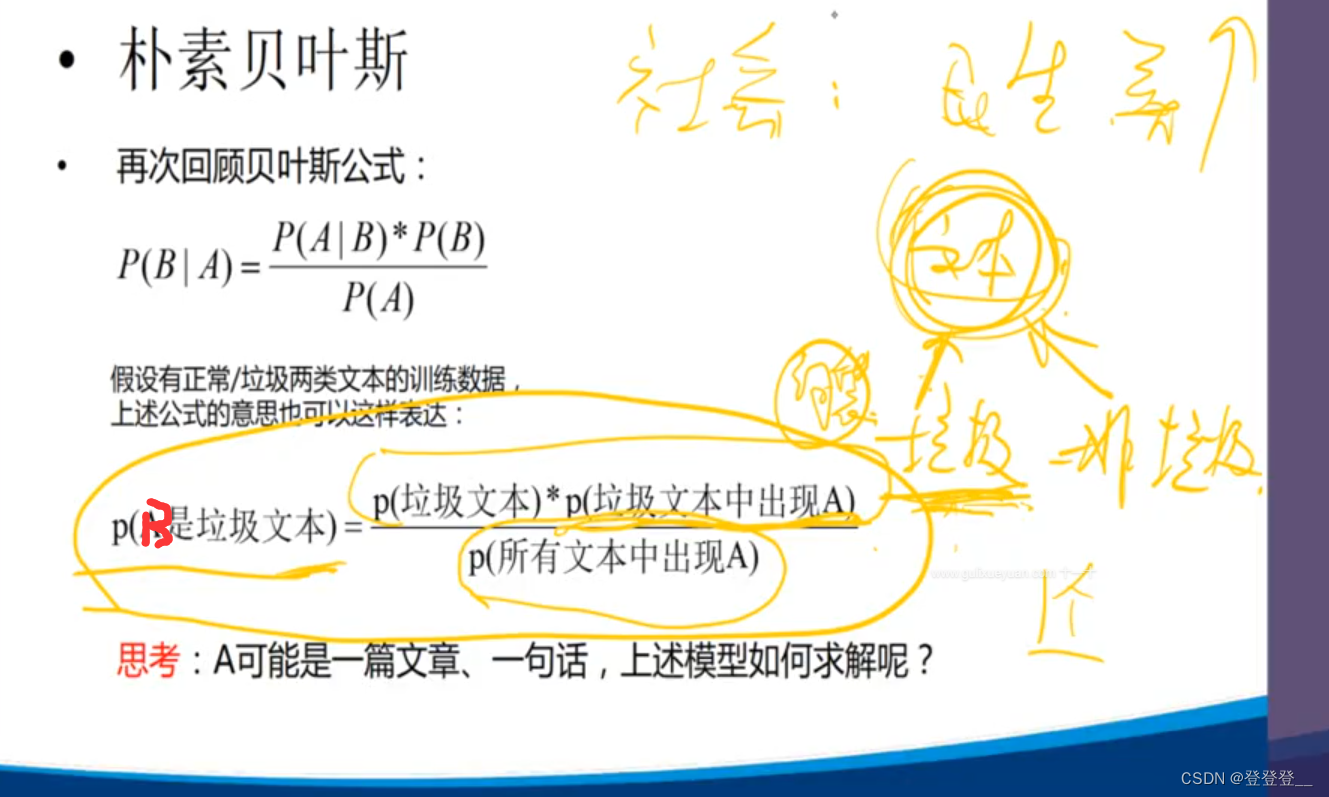
4.朴素贝叶斯算法(文本分类模型)
贝叶斯公式

LSTM模型(Long Short-Term Memory,长短期记忆)是一种特殊的RNN(循环神经网络),主要是为了解决长序列训练过程中的梯度消失和梯度模型(Long Short-Term Memory,长短期记忆)是一种特殊的RNN(循环神经网络),主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。
LSTM模型是一种强大的深度学习模型,特别适用于处理具有长期依赖关系的序列数据。
语言模型


马尔科夫假设



特点





![[Android]将私钥(.pk8)和公钥证书(.pem/.crt)合并成一个PKCS#12格式的密钥库文件](https://img-blog.csdnimg.cn/direct/254530f1f33f4653ba488c11ae8a58aa.png)