前言
思路及算法思维,指路 代码随想录。
题目来自 LeetCode。
day 21,天气不错的周二~
题目详情
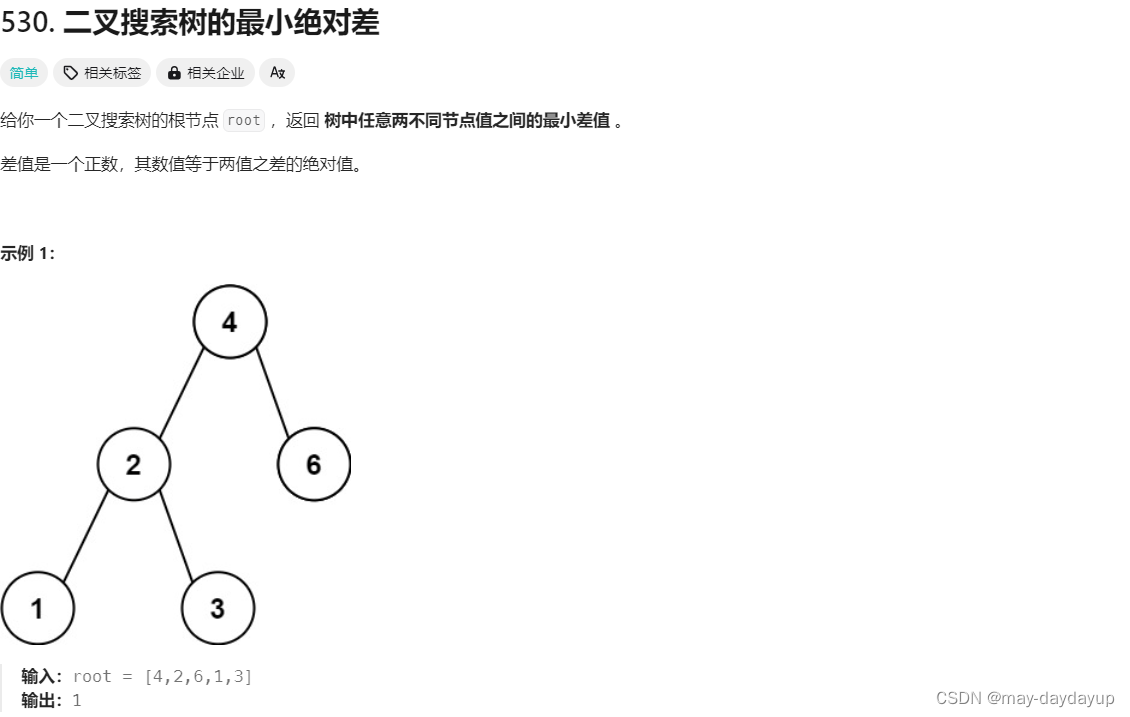
[530] 二叉搜索树的最小绝对差
题目描述
530 二叉搜索树的最小绝对差
解题思路
前提:二叉搜索树
思路:根据二叉搜索树的中序序列有序性,可以计算相邻结点的差值,最小即为所求。
重点:二叉搜索树特性。
代码实现
C语言
中序遍历 递归
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
void traversal(struct TreeNode *root, int *minVal, int *preVal)
{
// 判空
if (root == NULL)
{
return ;
}
// 中序遍历
// 左子树
traversal(root->left, minVal, preVal);
// 判断是否为最小值
if (*preVal == -1)
{
// 第一个结点
*preVal = root->val;
}
else
{
if ((root->val - *preVal) < *minVal)
{
*minVal = root->val - *preVal;
}
*preVal = root->val;
}
// 右子树
traversal(root->right, minVal, preVal);
return ;
}
int getMinimumDifference(struct TreeNode* root) {
int minVal = INT_MAX;
int preVal = -1;
traversal(root, &minVal, &preVal);
return minVal;
}
中序遍历 迭代栈
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int getMinimumDifference(struct TreeNode* root) {
int minVal = INT_MAX;
struct TreeNode *pre = NULL;
struct TreeNode *cur = root;
// 中序遍历 迭代栈
struct TreeNode *stack[10000];
int idx = 0;
while ((cur != NULL) || (idx != 0))
{
// 左节点
if (cur != NULL)
{
stack[idx++] = cur;
cur = cur->left;
}
else
{
// 中
cur = stack[--idx];
if (pre != NULL)
{
minVal = (minVal > (cur->val - pre->val)) ? (cur->val - pre->val) : minVal;
}
pre = cur;
// 右
cur = cur->right;
}
}
return minVal;
}
[501] 二叉搜索树的众数
题目描述
501 二叉搜索树的众数

解题思路
前提:二叉搜索树 含重复数值
思路:二叉搜索树中序序列非递减序列,判断数值出现频率最高的元素
重点:二叉搜索树中序序列非递减序列。
代码实现
C语言
中序遍历 递归
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
void traversal(struct TreeNode *root, int *nums, int *returnSize, int *maxSize, int *curNum, int *curSize)
{
// 判空
if (root == NULL)
{
return ;
}
// 中序遍历
// 左子树
traversal(root->left, nums, returnSize, maxSize, curNum, curSize);
// 中
if (root->val == *curNum)
{
// 当前遍历数值未发生变化,数量+1
(*curSize)++;
}
else
{
// 当前遍历数值发生变化,重新计数
*curSize = 1;
}
// 判断当前数值数量
if (*curSize >= *maxSize)
{
// 当前数值出现频率 > 当前最高频率
if (*curSize > *maxSize)
{
// 保存当前频率为最高频率,数量重新计数
*maxSize = *curSize;
*returnSize = 1;
}
else
{
// 当前数值出现频率 == 当前最高频率, 返回数量+1
(*returnSize)++;
}
// 赋值返回数组元素
nums[(*returnSize) - 1] = root->val;
}
// 保存当前数值,便于下一个节点判断
*curNum = root->val;
// 右子树
traversal(root->right, nums, returnSize, maxSize, curNum, curSize);
return ;
}
int* findMode(struct TreeNode* root, int* returnSize) {
*returnSize = 0;
int *nums = (int *)malloc(sizeof(int) * 10000);
int maxSize = 0;
int curNum = INT_MIN;
int curSize = 0;
traversal(root, nums, returnSize, &maxSize, &curNum, &curSize);
return nums;
}
[236] 二叉树的最近公共祖先
题目描述
236 二叉树的最近公共祖先

解题思路
前提:p、q均存在于二叉树上
思路:后序遍历,判断是否同处于某结点的左右子树上。
重点:有可能p、q为左右子树上,也有可能p为q的祖先。
代码实现
C语言
后序遍历 返回最近公共祖先
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
struct TreeNode *traversal(struct TreeNode *root, struct TreeNode* p, struct TreeNode* q)
{
// 判空
if ((root == NULL) || (p == NULL) || (q == NULL))
{
return NULL;
}
// 判断是否为该结点
if ((root == p) || (root == q))
{
return root;
}
// 左子树判断
struct TreeNode *leftNode = traversal(root->left, p, q);
// 右子树判断
struct TreeNode *rightNode = traversal(root->right, p, q);
// 判断是否遍历到了
if ((leftNode != NULL) && (rightNode != NULL))
{
// p、q位于root的左右两子树上,将root返回
return root;
}
if ((leftNode != NULL) && (rightNode == NULL))
{
// p、q至少其一位于root的左子树上,将leftNode返回,交由上层判断另一结点位置,有可能两节点均在该左子树上
return leftNode;
}
if ((rightNode != NULL) && (leftNode == NULL))
{
// p、q至少其一位于root的右子树上,将rightNode返回,交由上层判断另一结点位置,有可能两节点均在该右子树上
return rightNode;
}
// p、q均不位于root的左右两子树上
return NULL;
}
struct TreeNode* lowestCommonAncestor(struct TreeNode* root, struct TreeNode* p, struct TreeNode* q) {
struct TreeNode *ans = traversal(root, p, q);
return ans;
}
今日收获
- 二叉搜索树的中序遍历的使用
- 二叉树的最近公共祖先。