资源限制
内存限制:64.0MB C/C++时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s
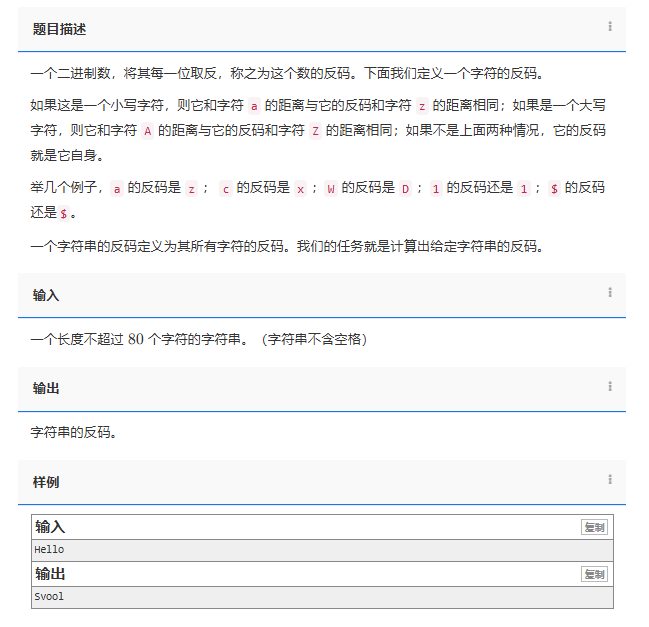
问题描述
给出一个n阶行列式(1<=n<=9),求出它的值。
输入格式
第一行给出两个正整数n,p;
接下来n行,每行n个数,表示行列式,数据保证行列式中每个数绝对值不超过2*10^9。
输出格式
一个数表示行列式的值,答案对p取余(余数需要是非负数)。
样例输入
2 2
5 -4
2 -1
样例输出
1
部分数据范围
对于20%的数据n<=2
对于40%的数据n<=3
对于100%的数据n<=9,p<=40000。
#include<iostream>
#include<math.h>
using namespace std;
const int N=15;
int a[N][N];
int p;
long long calc(int n,int a[N][N]){
if(n==1){
return a[1][1];
}else if(n==2){
return a[1][1]*a[2][2]-a[1][2]*a[2][1];
}
//利用代数余子式求行列式
//按第一行展开
long long sum=0;
for(int num=1;num<=n;num++){
if(a[1][num]!=0){//等于0就不需要计算了
//求代数余子式
int b_i=1;
int b[N][N];
for(int i=2;i<=n;i++){
int b_j=1;
for(int j=1;j<=n;j++){
if(j!=num){
b[b_i][b_j++]=a[i][j];
}
}
b_i++;
}
int det=calc(n-1,b);
sum+=pow(-1,1+num)*a[1][num]*det;
sum%=p;
}
}
return sum;
}
int main(){
int n;
cin>>n>>p;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
a[i][j]%=p;
}
}
long long sum=calc(n,a);
if(sum%p>=0){
cout<<sum%p<<endl;
}else{
cout<<p+sum%p<<endl;
}
return 0;
}
 思路:利用代数余子式求行列式的值。
思路:利用代数余子式求行列式的值。