判断链表是否带环
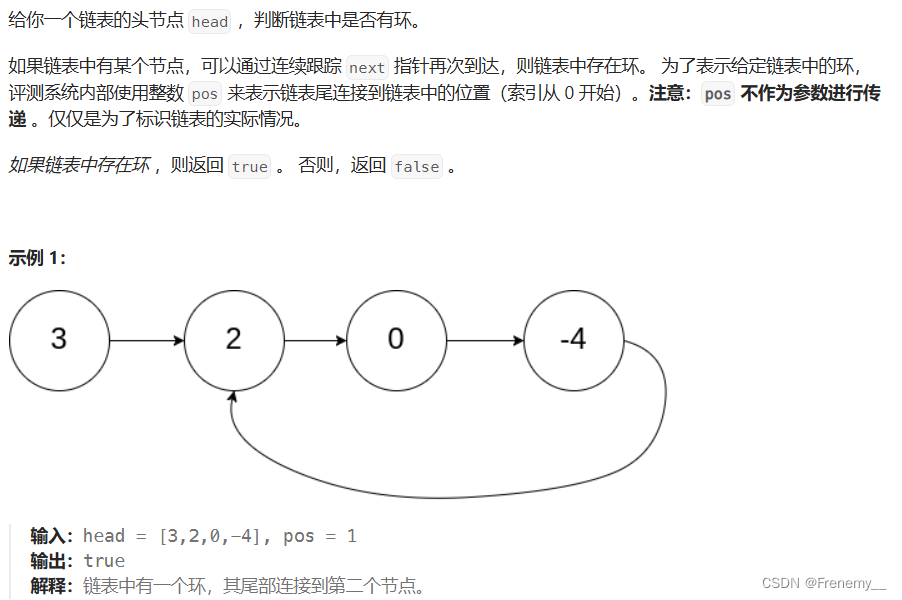
思路:快慢指针
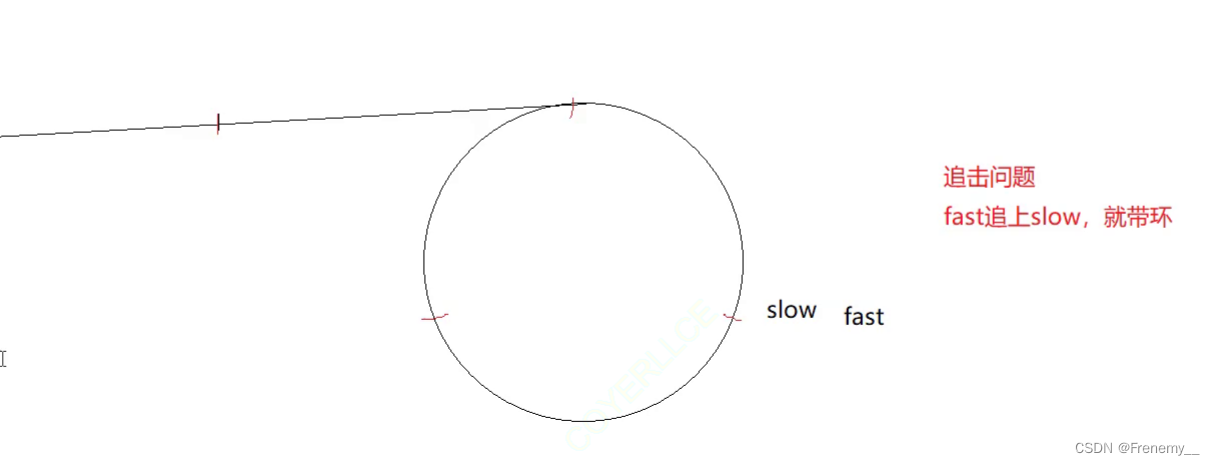
慢指针走一步,快指针走两步,当快指针追上慢指针时,代表该链表带环。代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
bool hasCycle(struct ListNode *head) {
struct ListNode *fast = head, *slow = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
{
return true;
}
}
return false;
}拓展
1.为什么一定会相遇?
证明:
当slow进入环时,不妨设fast与slow的距离为N,每一次slow和fast前进时,它们之间的距离每次减一,N、N-1、N-2...2、1、0.故一定会相遇。
2.slow一次走一步,fast一次走3步,4步等等可以吗?
证明:
当fast一次走3步
同上,当slow进环后,slow与fast的距离每次减2,当N为偶数时,可以追上;当N为奇数时,它们之间的距离会减少到-1,进行下一轮追及。此时不妨设环长C,它们之间的距离变成C-1,进行下一轮追及。
如果C-1时奇数
即C是奇数,它们之间的距离又会达到-1,永远不会追上。
如果C-1是偶数
即C为偶数,它们可以追上。
如果fast走4步,5步.......
通过fast % 3 == 0,fast % 3 == 1.......判断。
思考:它们真的会永远追不上吗?
前面我们证明了当C为偶数,N为奇数时,它们不会相遇,但C和N之间似乎也存在某种等量关系,这里我们对其进行证明:
假设slow进环后移动的距离是L,假设此时fast已经移动了x圈,则fast总共移动的距离为:L + x * C + C - N。又因为fast移动的距离是slow的3倍,于是我们可以列出一个表达式:
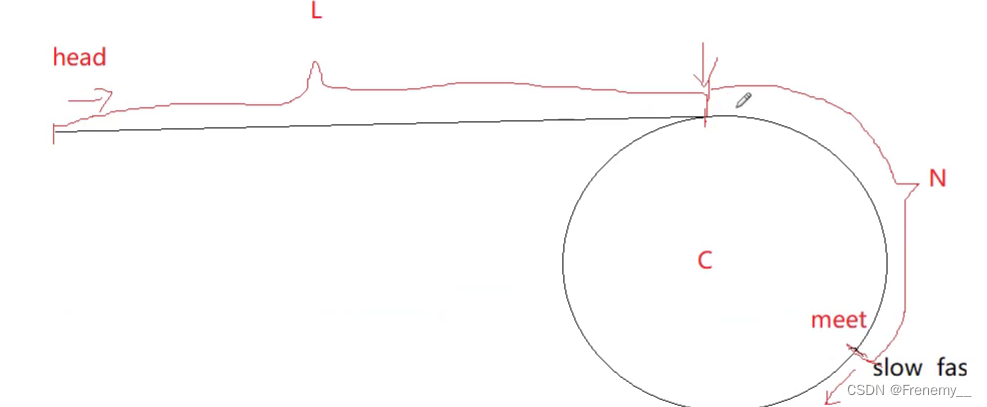
3L == L + x * C + C - N.化简可得 2L == (X + 1)*C - N,2L一定是偶数,(x+1)*C一定是偶数,N是奇数,于是我们发现,这个等式不可能存在:因为偶数不可能等于偶数减奇数。

综上,N是奇数且C是偶数不能同时存在,故当fast走3步时,一定可以追上。
寻找带环链表的环入口
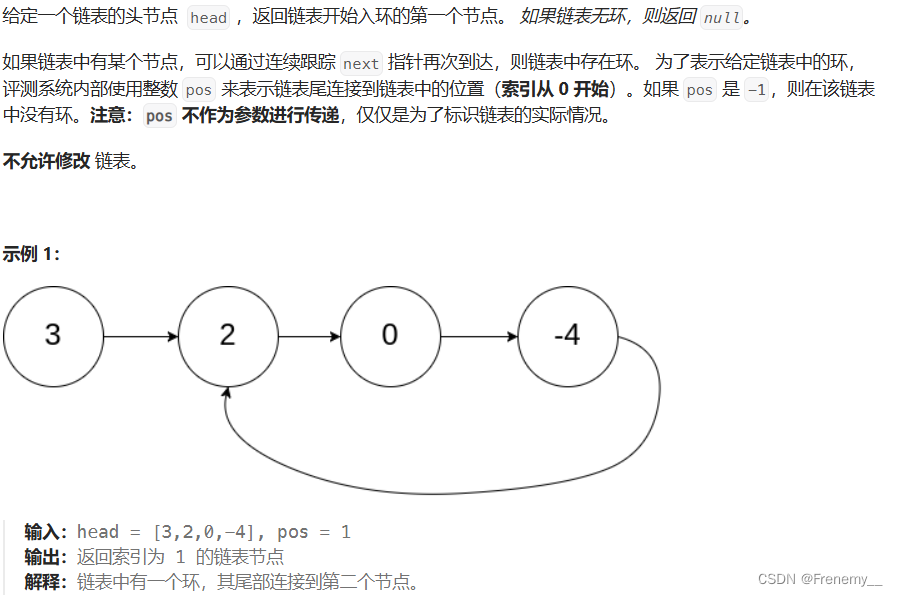
思路一:相遇节点
这里我们知道fast一次走两步,slow一次走一步时两指针一定会相遇,且一定是在slow移动的第一圈相遇,当slow指针移动到两指针相遇时,移动距离为:L + N。fast指针移动的距离为:L + N + x * C(x为fast已经移动的圈数)。联立得L = x * C - N。==》L = (x-1) * C + C - N此时相遇点的指针meet移动到入环节点的距离就是C-N == L。代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode *fast = head, *slow = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
{
struct ListNode *meet = slow;
while(meet != head)
{
meet = meet->next;
head = head->next;
}
return meet;
}
}
return NULL;
}思路二:转换为链表相交
我们可以将两指针相交节点的下一个节点设为meet,然后将相交节点指向空,目的是切断带环链表,将其转换为单链表,然后再通过判断链表相交函数实现返回链表带环的起始节点的目的。代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
struct ListNode *pcur1 = headA, *pcur2 = headB;
int len1 = 1, len2 = 1;
while(pcur1)
{
pcur1 = pcur1->next;
len1++;
}
while(pcur2)
{
pcur2 = pcur2->next;
len2++;
}
if(pcur1 != pcur2)
return NULL;
int gap = abs(len1 - len2);
struct ListNode* LongList = headA, *ShortList = headB;
if(len1 < len2)
{
LongList = headB;
ShortList = headA;
}
while(gap--)
{
LongList = LongList->next;
}
while(LongList != ShortList)
{
LongList = LongList->next;
ShortList = ShortList->next;
}
return LongList;
}
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode *fast = head, *slow = head;
while(fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
if(slow == fast)
{
struct ListNode *meet = slow->next;//找到相遇节点的下一个节点
slow->next = NULL;//切断链表
return getIntersectionNode(head, meet);
}
}
return NULL;//若没有则返回空
}综上,这道题,我们发现思路难,则代码简单;思路简单,则代码复杂。