1. LLM网址和prompt

deepseek网址

prompt

请用python写出以下程序：
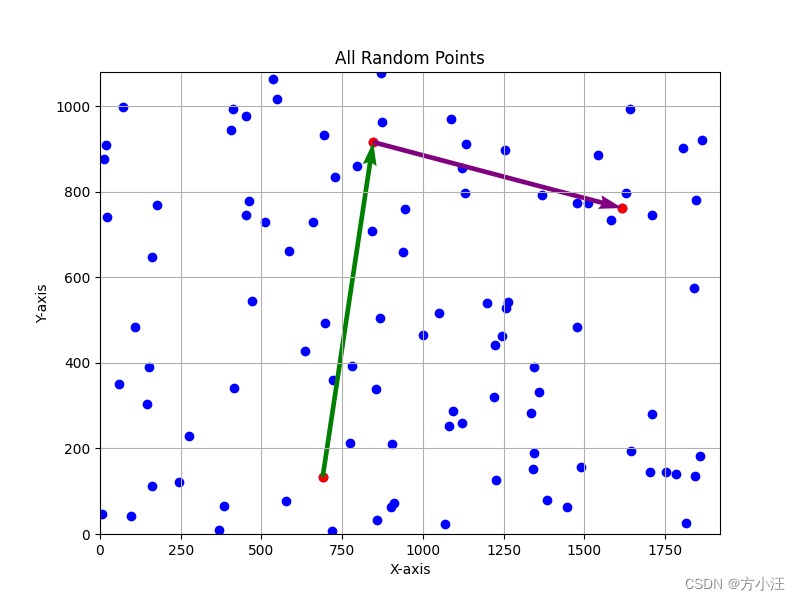
1、在x属于（0，1920）、y属于（0，1080）范围内，随机生成100个点，并画图
2、从这些点中选取3个点，使形成的两个向量以a的权重尽可能正交、以(1-a)/2的权重尽可能长度大、以(1-a)/2的权重尽可能长度接近，a=0.6

2. 生成code（有修改）

import random
import matplotlib.pyplot as plt
import numpy as np

# 生成10个随机点
points = []
for _ in range(100):
    x = random.uniform(0, 1920)
    y = random.uniform(0, 1080)
    points.append((x, y))

# # 生成100个随机点
# np.random.seed(0)  # 设置随机种子以确保可重复性
# points = np.random.rand(100, 2) * np.array([1920, 1080])

# 提取x和y坐标
x_coords, y_coords = zip(*points)

# 绘制所有点
plt.figure(figsize=(8, 6))
plt.scatter(x_coords, y_coords, color='blue', marker='o')
plt.title('All Random Points')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.grid(True)
plt.xlim(0, 1920)
plt.ylim(0, 1080)

# 权重系数
a = 0.6

# 计算所有可能的三个点组合的向量长度和正交性
best_points = None
best_score = -1

for i in range(len(points)):
    for j in range(i+1, len(points)):
        for k in range(j+1, len(points)):
            # 计算向量
            vector1 = (points[j][0] - points[i][0], points[j][1] - points[i][1])
            vector2 = (points[k][0] - points[j][0], points[k][1] - points[j][1])
            
            # 计算向量长度
            length1 = np.sqrt(vector1[0]**2 + vector1[1]**2)
            length2 = np.sqrt(vector2[0]**2 + vector2[1]**2)
            
            # 计算正交性
            orthogonality = np.abs(vector1[0]*vector2[0] + vector1[1]*vector2[1])

            # 计算长度接近度
            length_diff = np.abs(length1 - length2)
            
            # 计算综合得分
            score = a * (1 - orthogonality) + (1 - a) / 2 * (length1 + length2) + (1 - a) / 2 * (1 - length_diff / (length1 + length2))
            
            # 更新最佳组合
            if score > best_score:
                best_score = score
                best_points = (points[i], points[j], points[k])

# 绘制最佳组合的点
selected_x, selected_y = zip(*best_points)
plt.scatter(selected_x, selected_y, color='red', marker='o')

# 绘制向量
vector1_x = [best_points[0][0], best_points[1][0]]
vector1_y = [best_points[0][1], best_points[1][1]]
vector2_x = [best_points[1][0], best_points[2][0]]
vector2_y = [best_points[1][1], best_points[2][1]]

plt.quiver(vector1_x[0], vector1_y[0], vector1_x[1]-vector1_x[0], vector1_y[1]-vector1_y[0], angles='xy', scale_units='xy', scale=1, color='green')
plt.quiver(vector2_x[0], vector2_y[0], vector2_x[1]-vector2_x[0], vector2_y[1]-vector2_y[0], angles='xy', scale_units='xy', scale=1, color='purple')

plt.show()

3. 画图结果