边境牧羊犬优化算法(Border Collie Optimization,BCO)是一种受自然启发的群智能优化算法。该算法是通过模仿边境牧羊犬的放牧风格来开发的。本文成功地采用了边境牧羊犬从正面和侧面的独特放牧风格。在这个算法中,整个种群被分成两部分,即狗和羊。这样做是为了同时关注搜索空间的探索和利用。边境牧羊犬使用一种叫做“注视”的掠食动作。狗的这种技术被用来防止算法陷入局部最优。利用Sobol的灵敏度指标进行了灵敏度分析,该算法与蚁群算法、差分算法、遗传算法、灰狼优化器、哈里斯鹰优化器、粒子群优化器和鲸鱼优化算法等7种最先进的算法相比,该算法具有很强的竞争力。

该成果于2020年发表在知名SCI期刊“IEEE access”上,目前被引高达71次。

边界牧羊犬优化中,考虑了一个由三只狗和一只羊组成的种群。在现实生活中,一只狗就足以控制兽群。然而,由于不同优化问题的搜索空间可能很大,因此考虑了三个狗。在启动算法时,一个由三只狗和一只羊组成的群体被可视化。羊出去到不同的方向吃草,狗负责把它们带回农场。狗和羊的位置用随机变量初始化。狗分为领头狗、左狗和右狗是根据它们的位置来命名的。领头的狗从前面控制兽群。因此,在每次迭代中,具有最佳适应度的个体被指定为领头狗或羊群前面的狗。他们主要负责采集。

1、算法原理
(1)狗的速度 三只狗在时刻(t +1)的速度用下面的公式计算。
式中,Vf(t + 1)、Vri(t + 1)和Vle(t + 1)分别表示领头犬、右犬和左犬在(t + 1)时刻的速度。同理,Vf(t)、Vri(t)和Vle(t)分别表示导犬、左犬和右犬在t时刻的速度。Accf(t)、Accri(t)和Accle(t)分别表示导犬、右犬和左犬在t时刻的加速度。Popf(t)、Popri(t)和people (t)分别为时间(t)时领头狗、右狗和左狗的位置。
(2)羊的速度 利用三种放牧技术更新羊的速度。羊群聚集:离领头狗较近的羊群,向领头狗的方向移动。因此,这些羊只被收集起来。他们的选择是基于他们的健康值。
其中,dg的值为正,说明羊离领头狗更近。在这种情况下,羊的速度使用以下公式更新。
式中,羊群的速度Vsg直接受到时刻(t + 1)领头狗的速度和时刻(t)领头狗的加速度的影响。Popsg为待聚集羊群的当前位置。
跟踪:靠近左狗和右狗的羊,需要从两侧跟踪,以保持它们的轨道。这些羊是Dg值为负的羊。这些羊的速度更受左右狗的速度的影响。被跟踪的羊的速度更新方程如下所示。
式中,被跟踪的羊的速度,Vss取决于左右狗的速度。当狗从侧面引导羊群时,因此取随机穿越角的正切值θ1和θ2。θ1的取值范围为(1 ~ 89)度,θ2的取值范围为(91 ~ 179)度。θ1和θ2是随机选择的。
观察:那些完全误入歧途的羊是需要观察的。当在连续迭代中,个体的适应度没有提高时,实现了瞄准。在这种情况下,最不适合的狗被认为走在羊后面,给它们看一眼。因此,假设它们经历了发育迟缓,这可以用下面提到的方程来表示。
式中,Vle(t +1)和Accle(t)为左狗的速度和加速度,此时左狗在3只狗中适应度最差,Vri(t+1)和Accri(t)为右犬的速度、加速度,此时右犬在3只狗中适应度最小。Popse是要聚集的羊的当前位置。考虑最不适合的狗,因为假设这只狗离羊最近。
(3)狗和羊的加速度
加速度更新的方程来源于物理学中最常用的方程,如下所述。
所有狗和羊的加速度,即Accf(t + 1), Accri(t + 1), Accri(t + 1), Accsg(t + 1), Accss(t + 1)和Accse(t)使用(11)进行更新。I∈{f, le, ri, sg, ss至se}。
(4)狗和羊的时间
使用以下等式更新每个个体的遍历时间(T)。
其中,每个个体的平均遍历时间为维度(d)。
(5)狗的种群更新 使用位移的基本物理方程更新狗的位置。
在迭代过程中,下一次迭代的解用 表示,当前迭代的位置用Xi(t)表示。参数a计算为 ,其中randn表示正态分布中的随机数。N表示总体规模,Dim表示所考虑问题的维度。
公式更新了领头狗的位置,而左狗和右狗的位置使用(14)和式(15)更新。
(6)羊的种群更新 当羊属于聚集和跟踪群体时,使用以下公式更新羊的位置。
对于被注视的羊,使用下面提到的等式。
BCO优化算法的伪代码如下

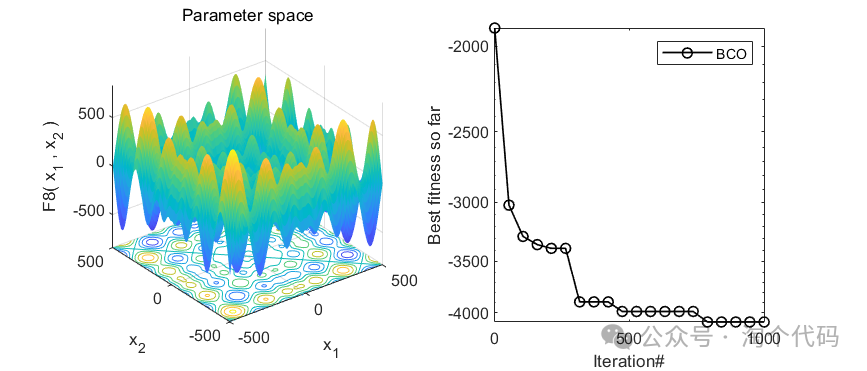
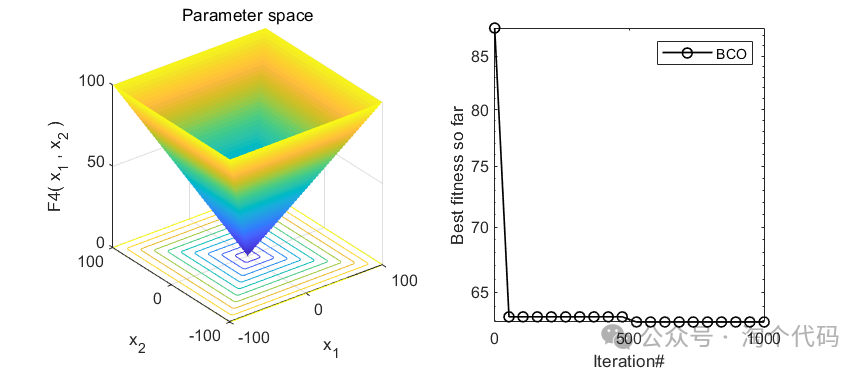
2、结果展示

3、MATLAB核心代码
%% 淘个代码 %%
% 微信公众号搜索:淘个代码,获取更多代码
% 边境牧羊犬优化算法(BCO)
%Border Collie Optimization
clear all;
%Population size
n=30;
%maximum no. of iterations
gen=200;
%Optimization function name
fname='func19';
%Retrieve function details(fobj), dimension(L), lower bound(lb) and upper bound(ub) of
%function
[lb,ub,L,fobj]=Func_details(fname);
%Intialize the population(initP-Population,acc-acceleration of each individual)
[initP,acc]=Generate(n,L,ub,lb);
%Vt=velocity of each individuals
Vt=(zeros(n,L));
%t=time of each individual
t=rand(n,1);
%Max. Fitness values
fopt=inf;
%Variable to store fitness
fit=zeros(1,n);
pop=initP;
%k=counter variable for iterations required for Eyeing mechanism
k=1;
fopt1=zeros(gen,1);
for g=1:gen
%Calculate fitness of individuals
[fit,maxf,pos]=Fitness(pop,n,L,ub,lb,fobj);
eye=0;
if g==1
fopt=maxf;
end
%finding the optimum fitness value
if fopt>maxf
fopt=maxf;
end
fopt1(g)=fopt;
if(g>1)
if(fopt1(g)>fopt1(g-1))
k=k+1;
if (k>5)
eye=1;
k=0;
end
end
end
%Sorting the dogs and sheep
[pop,Vt,fit,acc,t]=Herding(pop,Vt,fit,n,L,acc,t);
%Updating velocity, acceleration and time of the population
[Vt,acc,t,r1,l1,tempg,temps]=UpdateV(Vt,n,L,acc,t,pop,fit,eye);
%Updating positions of population
[pop]=Update(pop,Vt,t,acc,n,L,eye);
%Checking the range of the population is maintained
[pop,acc,t,Vt]=check(pop,n,L,ub,lb,acc,Vt,t);
fprintf('\n\nfopt %f\t maxf %f\tgen %d',fopt,maxf,g);
end参考文献
[1]Dutta T, Bhattacharyya S, Dey S, et al. Border collie optimization[J]. IEEE access, 2020, 8: 109177-109197.
完整代码获取
后台回复关键词:
TGDM833