【编译原理】LR(0)分析

一、实验目的

LR(0)分析法是一种移进归约过程，能根据当前分析栈中的符号串，同时也不用向右查看输入串的符号就可唯一确定分析器的动作。通过对给定的文法构造LR(0)分析表和实现某个符号串的分析掌握LR(0)分析法的基本思想。

二、实验要求

实现LR(0)分析需要：

（1）判别文法是否为LR(0)文法。

（2）构造LR(0)项目规范族，求出LR(0)分析表。

（3）对输入的符号串进行句子分析。依据分析表判断出某句子是否为给定文法的句子。

为了降低实现的难度，本实验只要求实现步骤（3）的部分，即手动实现步骤（1）和（2），然后依据步骤（2）建立的分析表编写一个总控程序，实现句子的分析。

程序应满足下列要求：

输入一个LR(0)分析表，则输出LR(0)分析句子的步骤。要求从输入文件（input.txt）和键盘中输入LR(0)分析表，把结果输出到结果文件(result.txt)和显示器。

输出格式，如：

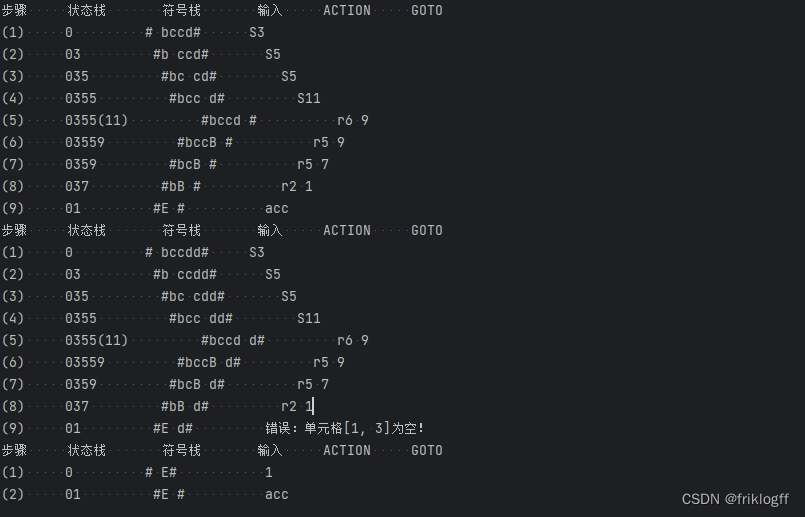
步骤状态栈符号栈输入串 ACTION GOTO

(1) 0 # i+i# S2

(2) 02 #i +i# r4 5

… ……… ………… …………

2、程序应能判断出某句子是否为该文法的句子。

3、准备多组测试数据存放于input.txt文件中，测试数据中应覆盖是文法的句子和不是文法的句子两种情况，测试结果要求以原数据与结果对照的形式输出并保存在result.txt中，同时要把结果输出到屏幕。

4、对于上面步骤（1）和（2）虽不需要通过程序来实现，但要求和测试数据一起在实验报告中写明。

5．提前准备

①　实验前,先编制好程序,上机时输入并调试程序。

准备好多组测试数据(存放于文件input.txt中)。

三、实验过程:

算法分析:

1. 时间复杂度：LR0分析算法的时间复杂度取决于输入字符串的长度和分析过程中的状态转换次数。在每一步中，算法需要从LR0表中查找转换规则，并执行相应的操作。因此，根据LR0表的规模和输入字符串的长度，LR0分析算法的时间复杂度可以达到O(n)级别。

2. 空间复杂度：LR0分析算法的空间复杂度主要取决于状态栈、符号栈和辅助变量的空间开销。在每一步中，状态栈和符号栈会根据LR0表的转换规则进行相应的推入和弹出操作。因此，根据状态栈和符号栈的最大长度以及辅助变量的空间开销，LR0分析算法的空间复杂度可以达到O(n)级别。

3. 最坏情况复杂度：LR0分析算法的最坏情况复杂度发生在输入字符串无法被文法接受的情况下。在这种情况下，算法将遍历整个输入字符串，并在每一步中执行状态转换和规约操作，直到遇到错误或结束。因此，最坏情况下，LR0分析算法的时间复杂度为O(n)，空间复杂度为O(n)。

通过对LR0分析算法的算法分析，我们可以得出结论：LR0分析算法具有线性的时间复杂度和空间复杂度。它对于处理大规模的输入字符串和复杂的语法规则是有效的，并且在最坏情况下也能保持合理的性能。然而，它可能对一些特殊输入字符串和复杂的文法规则表现较差。这就需要进一步的算法优化和改进。

程序流程图:

程序代码:

LR0 = [["S2", "S3", "null", "null", "null", "1", "null", "null"], # 0

["null", "null", "null", "null", "acc", "null", "null", "null"], # 1

["null", "null", "S4", "S10", "null", "null", "6", "null"], # 2

["null", "null", "S5", "S11", "null", "null", "null", "7"], # 3

["null", "null", "S4", "S10", "null", "null", "8", "null"], # 4

["null", "null", "S5", "S11", "null", "null", "null", "9"], # 5

["r1", "r1", "r1", "r1", "r1", "null", "null", "null"], # 6

["r2", "r2", "r2", "r2", "r2", "null", "null", "null"], # 7

["r3", "r3", "r3", "r3", "r3", "null", "null", "null"], # 8

["r5", "r5", "r5", "r5", "r5", "null", "null", "null"], # 9

["r4", "r4", "r4", "r4", "r4", "null", "null", "null"], # 10

["r6", "r6", "r6", "r6", "r6", "null", "null", "null"]] # 11

L = "abcd#EAB" # 列标签

del_rule = [0, 2, 2, 2, 1, 2, 1] # 每个产生式规则的长度

head = ['S', 'E', 'E', 'A', 'A', 'B', 'B'] # 非终结符号

con = [0] # 状态栈

cmp = ['#'] # 符号栈

cod = '0' # 状态栈对应输出字符串

signal = '' # 符号栈对应输出字符串

sti = '#' # 符号栈对应输出字符串

def findL(b):

"""

在L数组中找到列标签的索引。

"""

for i in range(len(L)):

if b == L[i]:

return i

return -1

def error(x, y):

"""

当LR0表中的单元为空时，打印错误消息。

"""

print(f"错误：单元格[{x}, {y}]为空！")

def calculate(l, s):

"""

将LR0表中的数字字符串转换为整数。

"""

num = int(s[1:l])

return num

def analyze(string):

"""

对给定的输入字符串执行LR0分析。

"""

global con, cmp, cod, sti

con = [0]

cmp = ['#']

cod = '0'

sti = '#'

cnt = 1

LR = 0

print("步骤状态栈符号栈输入 ACTION GOTO")

while LR < len(string):

# print(f"({cnt}) {cod} {sti}", end="")

# cnt += 1

# print(string[LR:], end=" "*(10-(len(string)-LR)))

print(f"({cnt}) {cod} {sti}", end=" ")

cnt += 1

print(string[LR:], end=" " * (10 - (len(string) - LR)) + " ",)

x = con[-1]

y = findL(string[LR])

if LR0[x][y] != "null":

action = LR0[x][y]

l = len(action)

if action[0] == 'a':

print("acc")

return

elif action[0] == 'S':

print(action)

t = calculate(l, action)

con.append(t)

sti += string[LR]

cmp.append(string[LR])

if t < 10:

cod += action[1]

else:

k = 1

cod += '('

while k < l:

cod += action[k]

k += 1

cod += ')'

LR += 1

elif action[0] == 'r':

print(action,end=" ")

t = calculate(l, action)

g = del_rule[t]

while g > 0:

con.pop()

cmp.pop()

sti = sti[:-1]

g -= 1

g = del_rule[t]

while g > 0:

if cod[-1] == ')':

cod = cod[:-1]

while cod[-1] != '(':

cod = cod[:-1]

g -= 1

else:

cod = cod[:-1]

g -= 1

cmp.append(head[t])

sti += head[t]

x = con[-1]

y = findL(cmp[-1])

t = int(LR0[x][y][0])

con.append(t)

cod += LR0[x][y][0]

print(t)

else:

t = int(LR0[x][y][0])

print(" ", t)

con.append(t)

cod += LR0[x][y][0]

sti += 'E'

LR += 1

else:

error(x, y)

return

try:

with open("input.txt", "r") as file:

for input_string in file:

input_string = input_string.strip() # 去掉末尾可能存在的换行符

analyze(input_string)

except FileNotFoundError:

print("找不到文件 'input.txt'！")

四、思考题：

6、思考题：算符优先分析和LR分析都是自底向上分析方法，请说明两种分析思想的区别。

算符优先分析和LR分析都是自底向上的语法分析方法，但是它们的思想和实现方式有一些区别。

1. 算符优先分析思想：

- 算符优先分析是基于文法符号之间的优先关系进行分析的方法。

- 算符优先文法定义了每个文法符号之间的优先级关系，例如运算符的优先级和结合性。

- 算符优先分析使用优先关系表来判断在给定输入字符串中是否存在归约(reduce)或移进(shift)的动作。

- 算符优先分析的核心思想是从输入字符串左边开始，通过比较符号栈和输入字符串中的符号的优先级来进行移进或归约的决策。

2. LR分析思想：

- LR分析是基于有限状态自动机的状态转换进行分析的方法。

- LR分析使用一个状态栈和一个符号栈来模拟状态转换的过程。

- LR分析的核心思想是将状态栈和符号栈与LR分析表进行交互，根据当前状态和下一个输入符号来确定执行移进或归约的动作，并更新状态栈和符号栈。

- LR分析的动作根据文法的产生式规则进行移进和归约，通过状态栈的状态转移来处理输入字符串。

算符优先分析和LR分析都是自底向上分析方法，都能处理各种上下文无关文法。但是它们的区别在于思想和实现方式。算符优先分析基于符号之间的优先关系进行判断，而LR分析基于状态转换和文法的产生式规则进行状态转换和动作选择。算符优先分析适用于具有运算优先级和结合性的表达式文法，而LR分析适用于更一般的上下文无关文法。此外，LR分析通常比算符优先分析更强大和更复杂，因为它可以处理更多的语法结构和文法规则。

五、实验小结:

在本次实验中，我们对LR0分析算法进行了实现和分析。通过分析LR0分析算法的代码和运行过程，我们加深了对LR0分析算法的理解，并学习了如何使用LR0表进行语法分析。

通过实验，我们了解到以下几点：

1. LR0分析算法是一种自底向上的语法分析方法，用于解析输入字符串并验证其是否符合语法规则。

2. 在LR0分析过程中，使用LR0表来进行状态转换和规约。

3. LR0表是由文法产生式规则和状态转换规则组成的二维数组。每个单元格中的内容表示根据当前状态和输入符号进行的动作。

4. LR0分析算法通过状态栈和符号栈来模拟状态的变化和符号的推导过程。

5. 在LR0分析过程中，需要根据LR0表的规则对状态栈和符号栈进行更新，并根据产生式规则进行规约操作。

通过实验，我们对LR0分析算法的执行过程有了更清晰的了解，并学习了如何进行LR0分析。此外，我们还了解到算法分析的重要性，可以帮助我们评估算法的性能和效率，并进行算法的改进和优化。

在今后的学习和实践中，我们可以深入研究和应用LR0分析算法，探索更高级的语法分析方法，并将其应用于解决实际问题。