【机器学习】随机梯度下降算法以及优化

一、概述：

什么是梯度下降？

梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上，需要从山上下来(i.e.找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，(同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走)。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

梯度的概念：

梯度是微积分中一个很重要的概念在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向这也就说明了为什么我们需要千方百计的求取梯度!我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的反方向一直走，就能走到局部的最低点。

梯度下降法中注意的点：

α-也就是步长

步长太小，下降太慢

步长太大，容易跳过极小值点

为什么梯度要加负号？

梯度方向是上升最快的方向，负号是下降最快的方向。

迭代次数和停止条件：

需要设置合适的迭代次数和停止条件，避免过度拟合或欠拟合。

停止条件可以设置为达到预设的迭代次数，或者当两次迭代之间的差值小于某个预设的阈值时停止。

初值的选择： 梯度下降法的初值选择会影响最终的结果。在实际应用中，可以尝试不同的初值来观察结果的差异。

二、常见的梯度下降算法：

1. 全梯度下降算法（FG）

计算训练集所有样本的误差，并对其求和取平均值作为目标函数，然后沿着目标函数的负梯度方向更新参数

通过迭代的方式，不断调整模型参数，使得损失函数的值逐渐减小，从而得到最优解。

权重向量沿其梯度相反的方向移动，从而使当前目标函数减少得最多。

因为在执行每次更新时，我们需要在整个数据集上计算所有的梯度，所以全梯度下降法的速度会很慢，同时，全梯度下降法无法处理超出内存容量限制的数据集。

全梯度下降法同样也不能在线更新模型，即在运行的过程中，不能增加新的样本。

其是在整个训练数据集上计算损失函数关于参数θ的梯度：

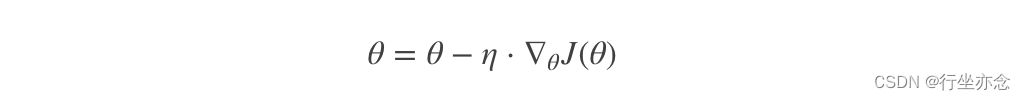
2. 随机梯度下降算法（SGD）

由于FG每迭代更新一次权重都需要计算所有样本误差，而实际问题中经常有上亿的训练样本，故效率偏低，且容易陷入局部最优解，因此提出了随机梯度下降算法。

随机梯度下降算法在每次迭代中，从训练集中随机选择一个样本来计算梯度，并据此更新模型参数。

其每轮计算的目标函数不再是全体样本误差，而仅是单个样本误差，即每次只代入计算一个样本目标函数的梯度来更新权重，再取下一个样本重复此过程，直到损失函数值停止下降或损失函数值小于某个可以容忍的阈值。

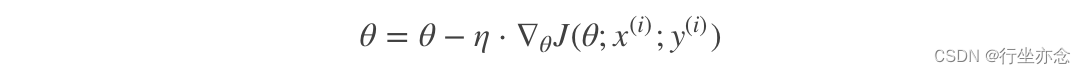
SGD特点：

计算效率高：由于每次迭代只使用一个样本，SGD的计算成本较低，可以处理大规模数据集。

收敛速度快：虽然SGD的收敛过程可能较为震荡，但由于其快速迭代的特点，通常能够在较短时间内达到一个较好的解。

对噪声敏感：由于每次迭代只使用一个样本，SGD对噪声和异常值较为敏感。可能收敛到局部最优解：与全梯度下降算法相比，SGD更有可能收敛到局部最优解而非全局最优解。

3. 小批量梯度下降算法（Mini-batch Gradient Descent）

是介于全梯度下降算法和随机梯度下降算法之间的一种优化算法，常用于深度学习和其他大规模机器学习问题的训练过程中。,在一定程度上兼顾了以上两种方法的优点。

小批量梯度下降算法在每次迭代中，从训练集中随机选择一小批（mini-batch）样本来计算梯度，并据此更新模型参数。

被抽出的小样本集所含样本点的个数称为batch_size，通常设置为2的幂次方，更有利于GPU加速处理。

特别的，若batch_size=1，则变成了SG；若batch_size=n，则变成了FG.其迭代形式为：

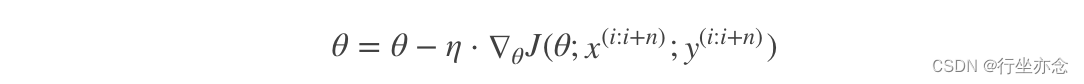
4.随机平均梯度下降算法（SAG）

在SG方法中，虽然避开了运算成本大的问题，但对于大数据训练而言，SG效果常不尽如人意，因为每一轮梯度更新都完全与上一轮的数据和梯度无关。

随机平均梯度算法克服了这个问题，在内存中为每一个样本都维护一个旧的梯度，随机选择第i个样本来更新此样本的梯度，其他样本的梯度保持不变，然后求得所有梯度的平均值，进而更新了参数。

通过随机选择样本来更新梯度和模型参数，但与传统SGD不同的是，SAG利用了数据的重复利用，在每次迭代中都会更新所有样本的梯度，并使用这些梯度的平均值来更新模型参数。这样可以减小每次更新的方差，提高算法的稳定性，收敛速度也比SGD快。

5.算法比较

为了比对四种基本梯度下降算法的性能，我们通过一个逻辑二分类实验来说明。数据集共有15081条记录，包括“性别”“年龄”“受教育情况”“每周工作时常”等14个特征，数据标记列显示“年薪是否大于50000美元”。我们将数据集的80%作为训练集，剩下的20%作为测试集，使用逻辑回归建立预测模型，根据数据点的14个特征预测其数据标记（收入情况）。

以下6幅图反映了模型优化过程中四种梯度算法的性能差异。

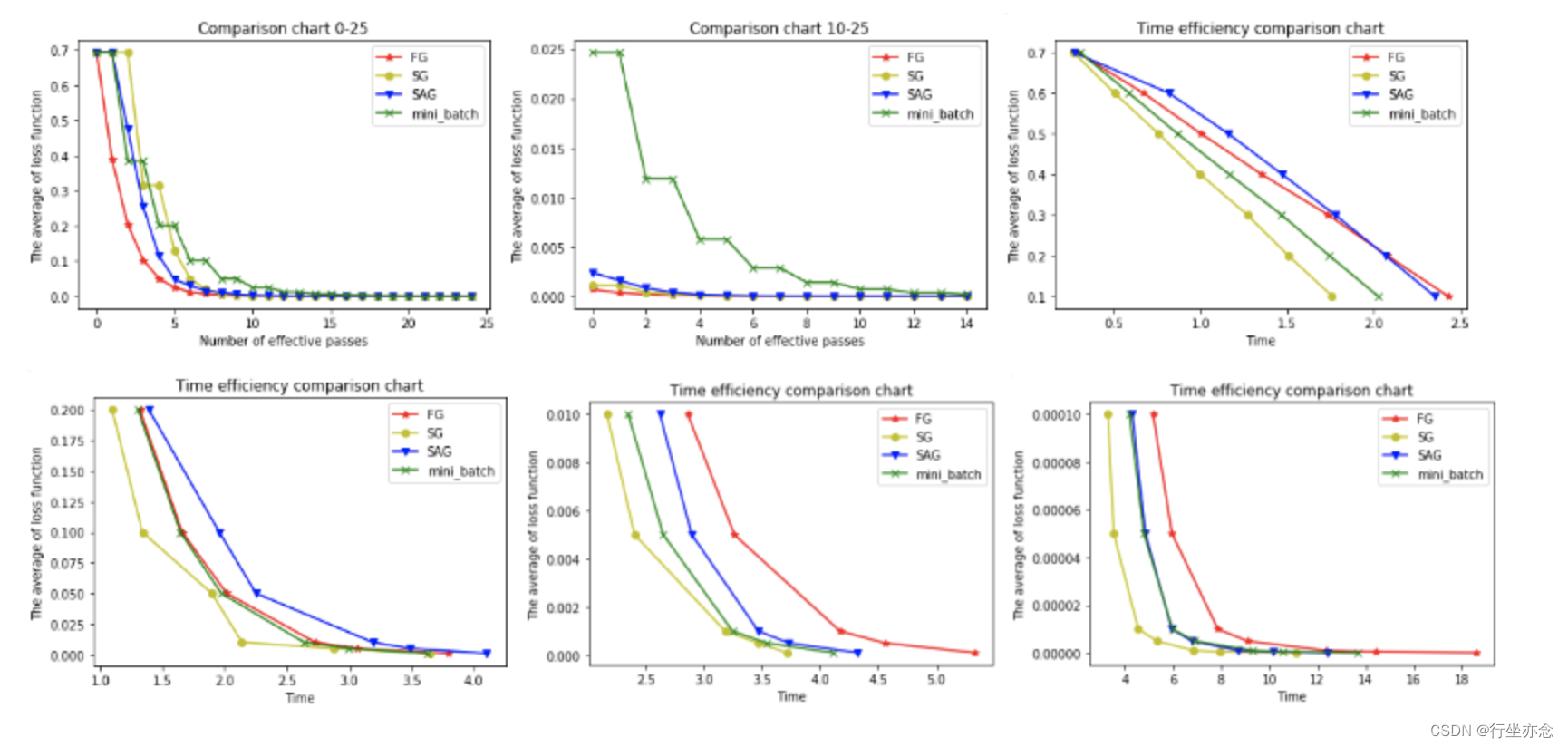
在图1和图2中，横坐标代表有效迭代次数，纵坐标代表平均损失函数值。图1反映了前25次有效迭代过程中平均损失函数值的变化情况，为了便于观察，图2放大了第10次到25次的迭代情况。

从图1中可以看到，四种梯度算法下，平均损失函数值随迭代次数的增加而减少。FG的迭代效率始终领先，能在较少的迭代次数下取得较低的平均损失函数值。FG与SAG的图像较平滑，这是因为这两种算法在进行梯度更新时都结合了之前的梯度；SG与mini-batch的图像曲折明显，这是因为这两种算法在每轮更新梯度时都随机抽取一个或若干样本进行计算，并没有考虑到之前的梯度。

从图2中可以看到虽然四条折现的纵坐标虽然都趋近于0，但SG和FG较早，mini-batch最晚。这说明如果想使用mini-batch获得最优参数，必须对其进行较其他三种梯度算法更多频次的迭代。

在图3，4，5，6中，横坐标表示时间，纵坐标表示平均损失函数值。

从图3中可以看出使用四种算法将平均损失函数值从0.7降到0.1最多只需要2.5s，由于本文程序在初始化梯度时将梯度设为了零，故前期的优化效果格外明显。其中SG在前期的表现最好，仅1.75s便将损失函值降到了0.1，虽然SG无法像FG那样达到线性收敛，但在处理大规模机器学习问题时，为了节约时间成本和存储成本，可在训练的一开始先使用SG，后期考虑到收敛性和精度可改用其他算法。

从图4，5，6可以看出，随着平均损失函数值的不断减小，SG的性能逐渐反超FG，FG的优化效率最慢，即达到相同平均损失函数值时FG所需要的时间最久。

综合分析六幅图我们得出以下结论：

（1）FG方法由于它每轮更新都要使用全体数据集，故花费的时间成本最多，内存存储最大。

（2）SAG在训练初期表现不佳，优化速度较慢。这是因为我们常将初始梯度设为0，而SAG每轮梯度更新都结合了上一轮梯度值。

（3）综合考虑迭代次数和运行时间，SG（随机梯度下降，也叫SGD）表现性能都很好，能在训练初期快速摆脱初始梯度值，快速将平均损失函数降到很低。但要注意，在使用SG方法时要慎重选择步长，否则容易错过最优解。

（4）mini-batch结合了SG的“胆大”和FG的“心细”，从6幅图像来看，它的表现也正好居于SG和FG二者之间。在目前的机器学习领域，mini-batch是使用最多的梯度下降算法，正是因为它避开了FG运算效率低成本大和SG收敛效果不稳定的缺点。

三、梯度下降优化算法

以下这些算法主要用于深度学习优化：

1.动量法

动量法（Momentum Method）是对传统梯度下降算法的一种改进，旨在解决梯度下降算法中收敛速度慢和容易陷入局部最优解的问题。动量法通过引入一个动量项来加速优化过程，并减少震荡现象。

$(v(t) = \beta v(t-1) + (1-\beta) \nabla L(w(t)))$

(v(t)) 表示第 (t) 步迭代时的动量。

( $\beta$ ) 是动量因子，通常取值在0.9左右。

( $\nabla L(w(t))$ ) 是损失函数 (L) 在当前参数 (w(t)) 下的梯度。

$(w(t+1) = w(t) - \eta v(t))$

(w(t)) 和 (w(t+1)) 分别表示第 (t) 步和第 (t+1) 步迭代时的参数值。

( $\eta$ ) 是学习率，控制每一步迭代的步长。

2.Adam算法

原理：

Adam（自适应矩估计）算法的基本思想是在梯度下降算法的基础上，引入两个动量变量来分别保存梯度的一阶矩估计和二阶矩估计，从而实现对学习率的自适应调整。具体来说，一阶矩估计类似于传统动量法中的动量项，用于加速参数更新；二阶矩估计则类似于RMSProp算法中的梯度平方的平均值，用于调整学习率的大小。

优化步骤：

1.计算梯度：

     使用训练数据进行前向传播。

     计算损失函数对模型参数的梯度。

2.更新动量：

     一阶矩估计（动量项）：记录历史梯度的加权平均，用于平滑梯度更新。

     二阶矩估计（梯度平方的平均值）：记录梯度平方的加权平均，用于调整学习率的大小。

3.偏差修正：

     由于初始时动量值为0，Adam算法引入偏差修正来避免初期偏差。

     对一阶矩估计和二阶矩估计进行修正。

4.参数更新：

     使用修正后的一阶矩估计（动量项）和二阶矩估计（梯度平方的平均值）来更新模型的参数。

     公式中的学习率、小常数和当前迭代步数等因素共同决定了参数更新的幅度和方向。

Adam优化算法对内存的需求很小，它结合了动量项，有效减少了训练过程中的震荡，并通过计算一阶和二阶矩估计自适应地调整每个参数的学习率。这种灵活性使得Adam能够针对不同参数设置最适合的学习步长，从而提高训练效率和模型性能。因此，Adam算法在各种深度学习任务中都表现出色，成为当今深度学习领域最受欢迎的优化算法之一。