目录
一、相关概念
性质
二、图解
1、插入操作
2、parent在左边情况1:cur为红色节点parent也是红色节点、uncle也为红色节点
3、parent在左边情况2:cur为红色节点parent也是红色节点、uncle为黑色或者是空,cur是parent的left
4、parent在左边情况3:cur为红色节点parent也是红色节点、uncle为黑色或者是空,cur是parent的right
5、parent在右边情况1:cur为红色节点parent也是红色节点、uncle也为红色节点
6、parent在右边情况2:cur为红色节点parent为红色节点、uncle为黑色或者是空,cur是parent的right
7、parent在右边情况3:cur为红色节点parent为红色节点、uncle为黑色或者是空,cur是parent的left
三、代码实现
1、准备节点
2、实现插入
3、 代码实现
一、相关概念
红黑树是一种自平衡的二叉查找树。
红黑树是计算机科学中广泛使用的数据结构,通常用于实现关联数组等数据结构,以保证在最坏情况下仍具有较好的查找性能。下面是其特点和性质:
- 节点颜色:每个节点都有一个颜色属性,可以是红色或黑色。
- 根节点为黑:红黑树的根节点总是黑色的。
- 叶节点为黑:所有叶子节点(NIL)都是黑色的。这里的叶子节点指的是没有子节点的空链接。
- 路径长度限制:从根节点到任何叶子节点的简单路径上,均不会出现两个连续的红色节点,这意味着没有任何一个路径会比其它路径长出两倍。
- 查找效率:红黑树可以在 O(log N) 时间内完成查找、增加、删除等操作,其中 N 是树中元素的数量。
此外,红黑树的本质是对概念模型2-3-4树的一种实现。2-3-4树是阶数为4的B树,也是平衡多路查找树的一种,它通过保持树的平衡来确保即使在最坏情况下也能保持 O(Log N) 的时间复杂度进行查找操作。
性质
- 最长路径是最短路径的2倍
- 根节点是黑色的
- 如果一个节点是红色的,那么他的两个孩子节点是黑色的
- 对于每个节点,该节点到其所有后代的叶子节点的简单路径上均包含相同数目的黑色节点
二、图解
1、插入操作
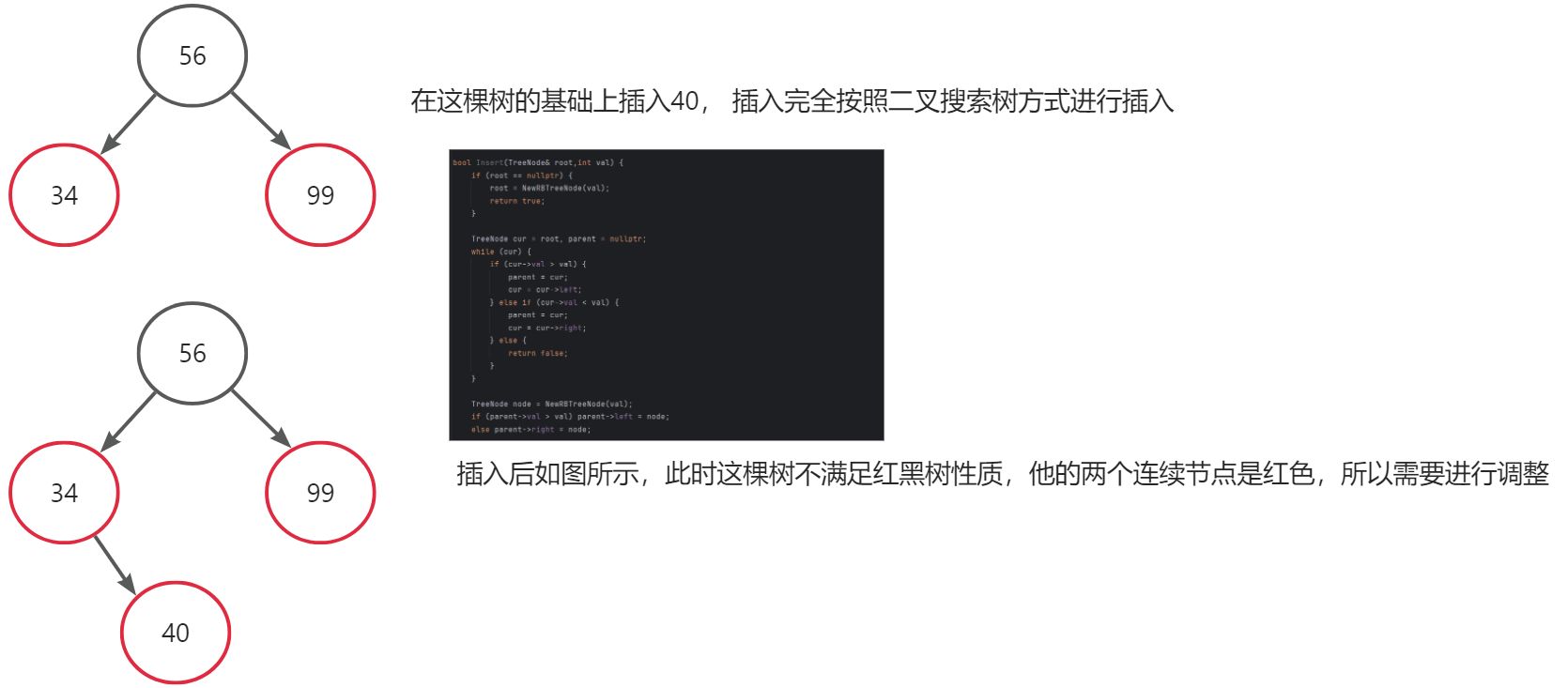
每次插入节点的颜色都为红色,按照二叉搜索树的方式插入后,开始从插入的节点向上调整,使得这棵树满足红黑树上述的性质,在进行调整的过程中大致左右树类似分为3中情况,在调整之前的插入部分图解如下:
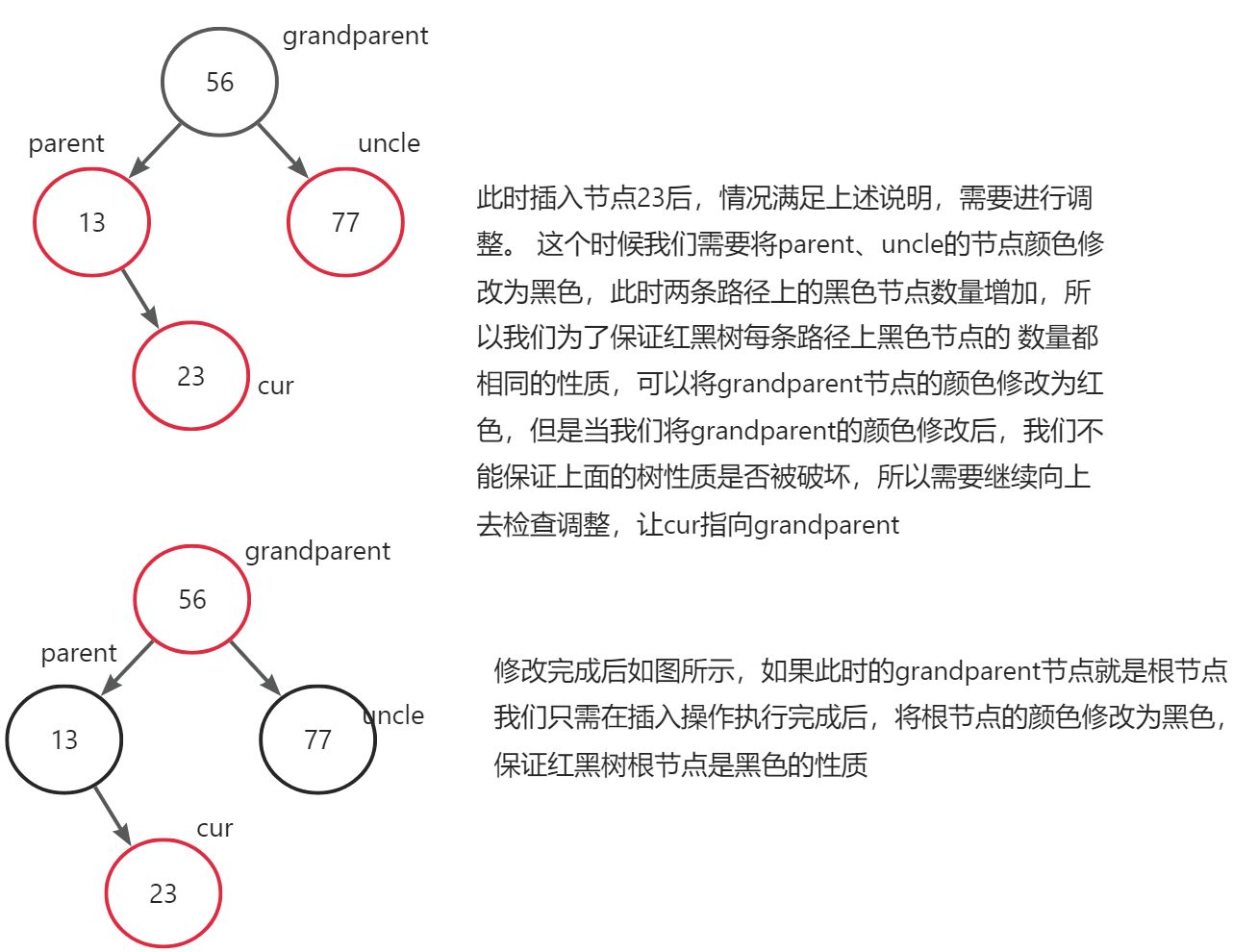
2、parent在左边情况1:cur为红色节点parent也是红色节点、uncle也为红色节点
3、parent在左边情况2:cur为红色节点parent也是红色节点、uncle为黑色或者是空,cur是parent的left
这种情况不可能是刚插入cur节点而引起的,因为此时grandparent是黑色的,此时parent路径上比uncle路径上的黑色节点少一个,所以这种情况是发生在调整的过程中的。
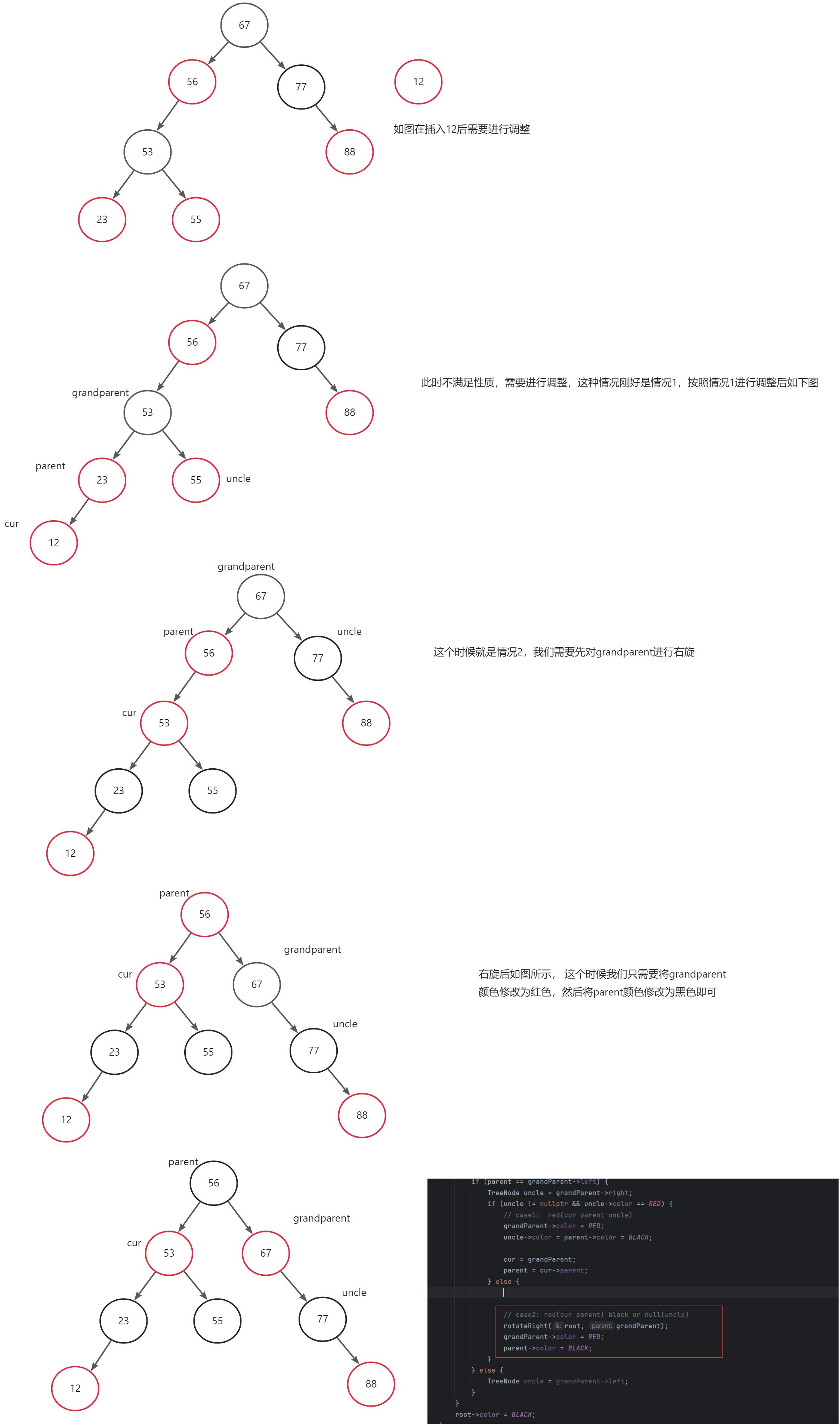
4、parent在左边情况3:cur为红色节点parent也是红色节点、uncle为黑色或者是空,cur是parent的right
这种情况也是发生在向上调整的过程中的
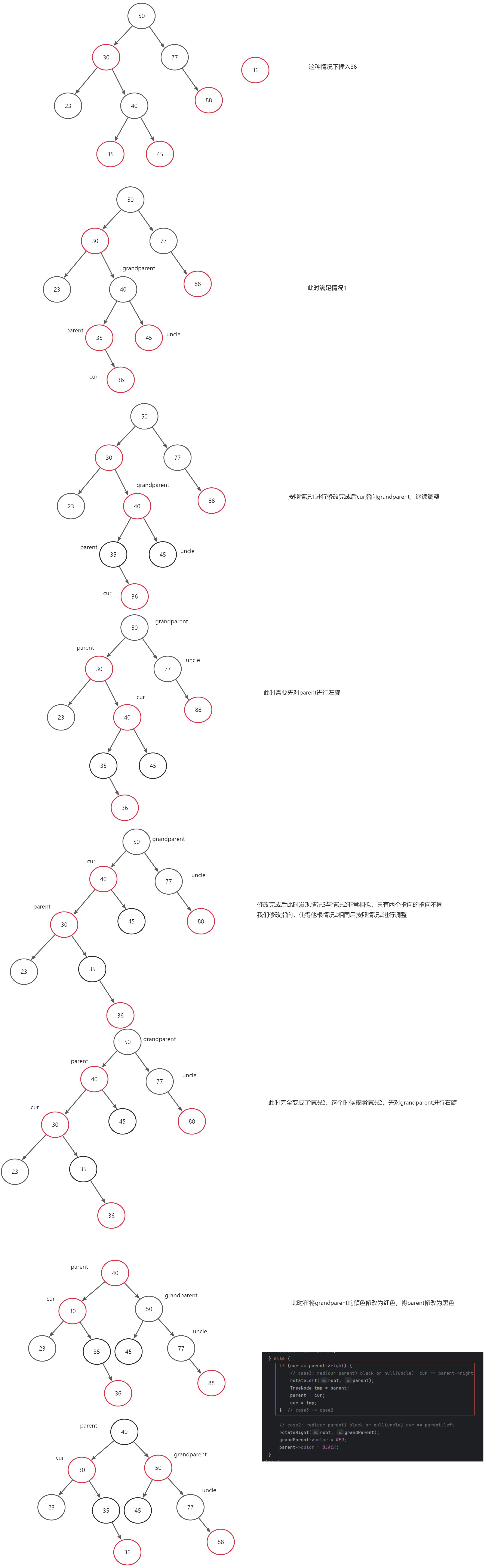
5、parent在右边情况1:cur为红色节点parent也是红色节点、uncle也为红色节点
与parent是grandparent的左边类型,右边的操作全部镜像

6、parent在右边情况2:cur为红色节点parent为红色节点、uncle为黑色或者是空,cur是parent的right
与上述parent是grandparent左边的情况2镜像相同,同样发生在调整的 过程中
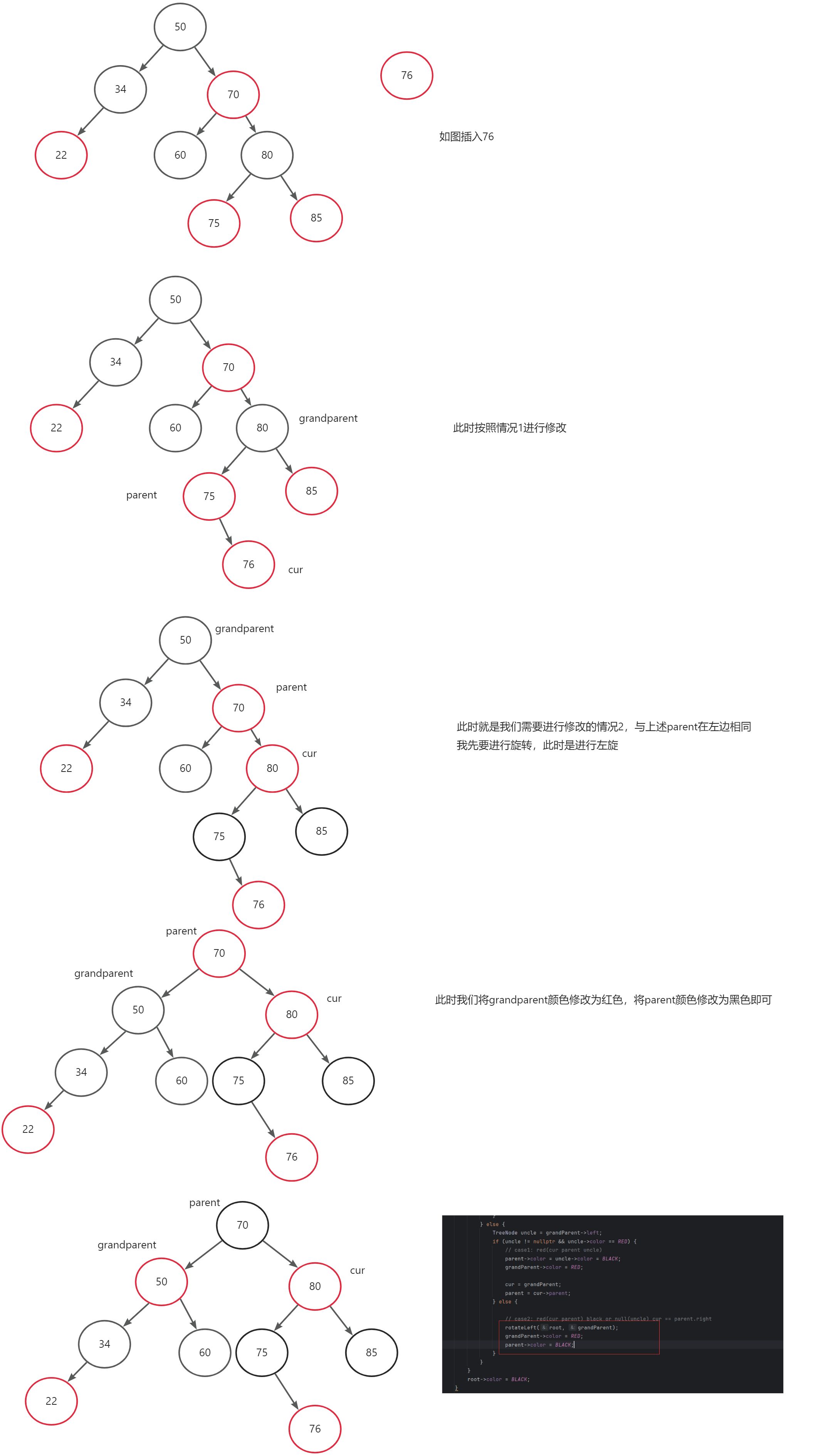
7、parent在右边情况3:cur为红色节点parent为红色节点、uncle为黑色或者是空,cur是parent的left
与上述情况类型,将情况3转变为情况2去处理
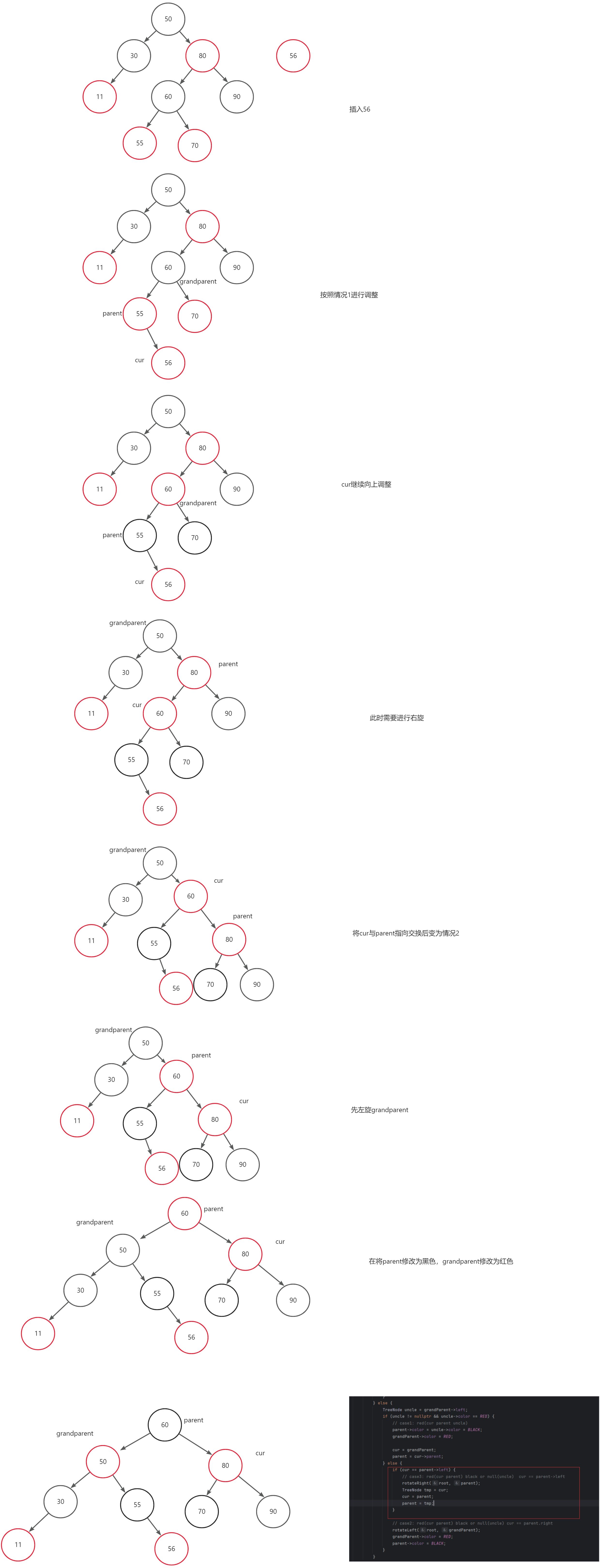
三、代码实现
1、准备节点
首先一颗红黑树的节点需要哪些字段呢?需要数据域,以及左孩子指针右孩子指针还需存储他的父亲节点的指针,其次就是这个节点颜色
1.字段
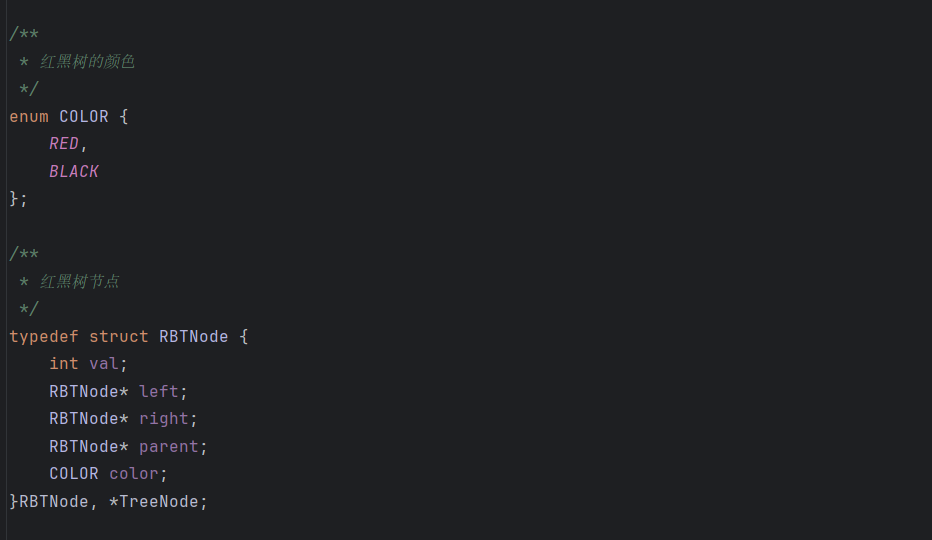
2、实现插入
首先红黑树的插入主要分为两步将节点按照红色进行插入,插入方法与二叉搜索树插入相同。插入完成后按照其性质进行调整(左右旋转图示详解在AVL树)
插入
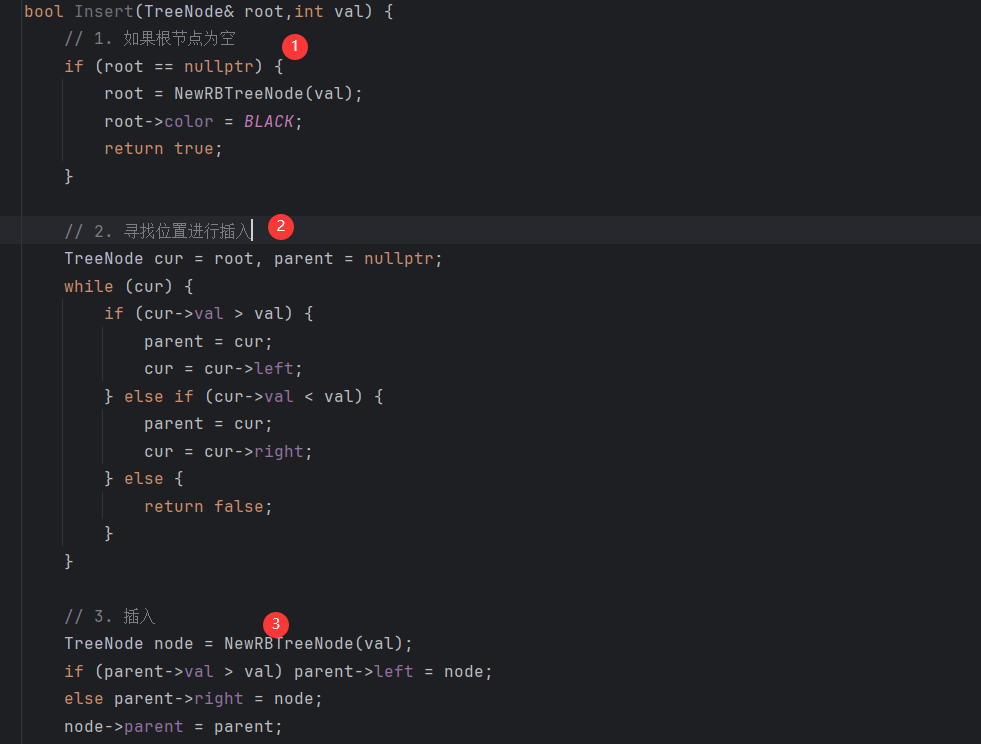
调整
插入节点颜色是红色,此时如果他的父亲节点也是红色,那么就不满足红黑树的性质,此时就需要去进行分情况调整,主要情况在二中详细图示
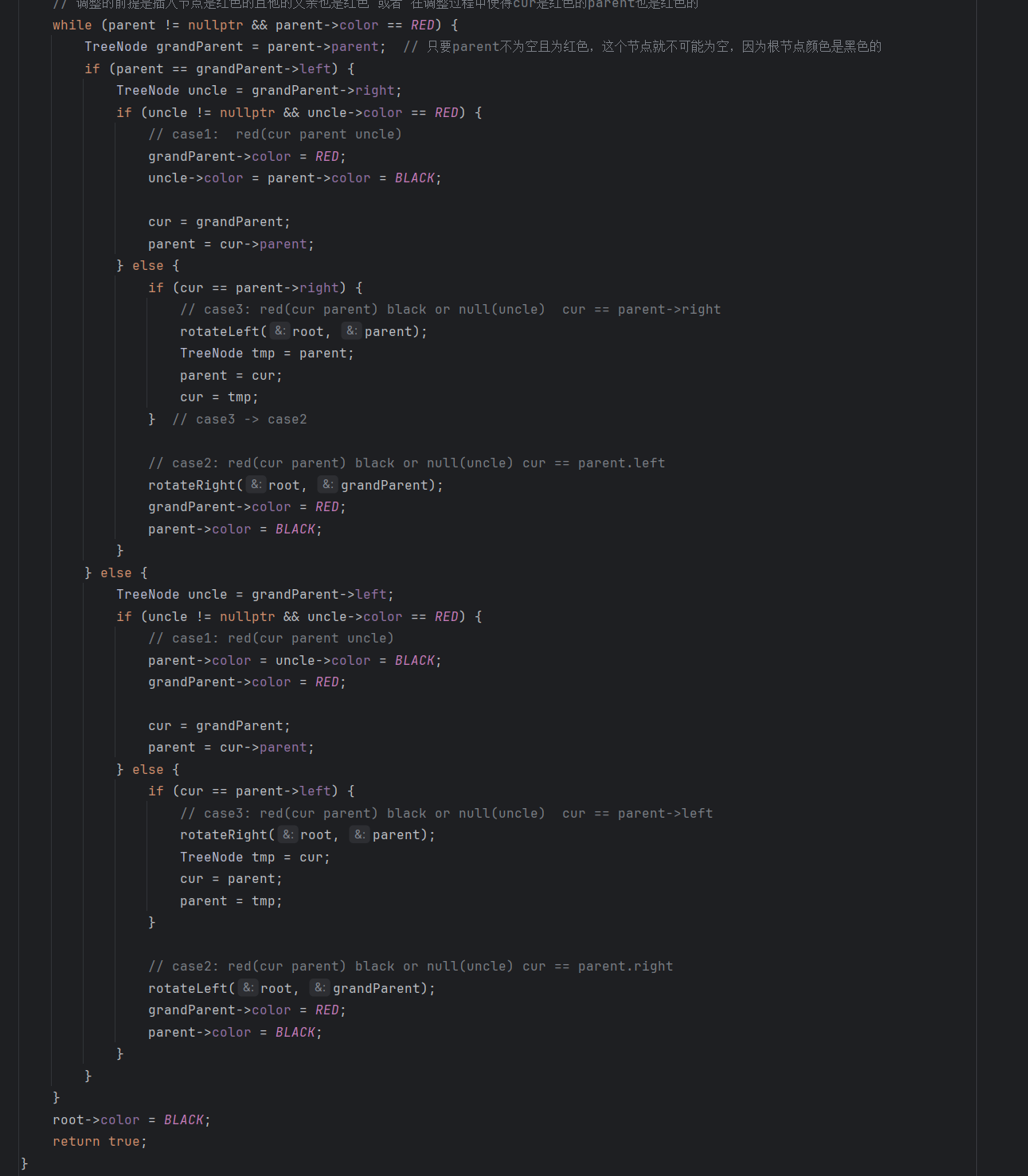
3、 代码实现
#include<iostream>
using namespace std;
/**
* 红黑树的颜色
*/
enum COLOR {
RED,
BLACK
};
/**
* 红黑树节点
*/
typedef struct RBTNode {
int val;
RBTNode* left;
RBTNode* right;
RBTNode* parent;
COLOR color;
}RBTNode, *TreeNode;
/**
* 创建并初始化一个根节点
* @param val
* @return
*/
TreeNode NewRBTreeNode (int val) {
auto node = (TreeNode) malloc(sizeof(RBTNode));
node->val = val;
node->color = RED;
node->left = node->right = node->parent = nullptr;
return node;
}
/**
* 右旋
* @param root 根节点
* @param parent 旋转节点
*/
void rotateRight(TreeNode& root, TreeNode& parent) {
TreeNode subL = parent->left;
TreeNode subLR = subL->right;
TreeNode pParent = parent->parent;
parent->left = subLR;
subL->right = parent;
if (subLR != nullptr) subLR->parent = parent;
parent->parent = subL;
if (parent == root) {
root = subL;
subL->parent = nullptr;
} else if (parent == pParent->left) {
pParent->left = subL;
subL->parent = pParent;
} else {
pParent->right = subL;
subL->parent = pParent;
}
}
/**
* 左旋
* @param root 根节点
* @param parent 旋转节点
*/
void rotateLeft(TreeNode& root, TreeNode& parent) {
TreeNode subR = parent->right;
TreeNode subRL = subR->left;
TreeNode pParent = parent->parent;
parent->right = subRL;
subR->left = parent;
if (subRL != nullptr) subRL->parent = parent;
parent->parent = subR;
if (parent == root) {
root = subR;
subR->parent = nullptr;
} else if (parent == pParent->left) {
pParent->left = subR;
subR->parent = pParent;
} else {
pParent->right = subR;
subR->parent = pParent;
}
}
/**
* 插入
* @param root 根节点
* @param val 要插入的元素
* @return
*/
bool Insert(TreeNode& root,int val) {
if (root == nullptr) {
root = NewRBTreeNode(val);
root->color = BLACK;
return true;
}
TreeNode cur = root, parent = nullptr;
while (cur) {
if (cur->val > val) {
parent = cur;
cur = cur->left;
} else if (cur->val < val) {
parent = cur;
cur = cur->right;
} else {
return false;
}
}
TreeNode node = NewRBTreeNode(val);
if (parent->val > val) parent->left = node;
else parent->right = node;
node->parent = parent;
cur = node;
// 调整的前提是插入节点是红色的且他的父亲也是红色 或者 在调整过程中使得cur是红色的parent也是红色的
while (parent != nullptr && parent->color == RED) {
TreeNode grandParent = parent->parent; // 只要parent不为空且为红色,这个节点就不可能为空,因为根节点颜色是黑色的
if (parent == grandParent->left) {
TreeNode uncle = grandParent->right;
if (uncle != nullptr && uncle->color == RED) {
// case1: red(cur parent uncle)
grandParent->color = RED;
uncle->color = parent->color = BLACK;
cur = grandParent;
parent = cur->parent;
} else {
if (cur == parent->right) {
// case3: red(cur parent) black or null(uncle) cur == parent->right
rotateLeft(root, parent);
TreeNode tmp = parent;
parent = cur;
cur = tmp;
} // case3 -> case2
// case2: red(cur parent) black or null(uncle) cur == parent.left
rotateRight(root, grandParent);
grandParent->color = RED;
parent->color = BLACK;
}
} else {
TreeNode uncle = grandParent->left;
if (uncle != nullptr && uncle->color == RED) {
// case1: red(cur parent uncle)
parent->color = uncle->color = BLACK;
grandParent->color = RED;
cur = grandParent;
parent = cur->parent;
} else {
if (cur == parent->left) {
// case3: red(cur parent) black or null(uncle) cur == parent->left
rotateRight(root, parent);
TreeNode tmp = cur;
cur = parent;
parent = tmp;
}
// case2: red(cur parent) black or null(uncle) cur == parent.right
rotateLeft(root, grandParent);
grandParent->color = RED;
parent->color = BLACK;
}
}
}
root->color = BLACK;
return true;
}