基于何明凯前辈论文的学习

1.主要内容（背景）

1、首先提了一个base：神经网络的深度越深，越难以训练。
2、原因：因为随着神经网络层数的增加，通常会遇到梯度消失或梯度爆炸等问题，这会导致训练变得更加困难。梯度消失指的是：在反向传播过程中，梯度逐渐变得非常小，以至于无法有效地更新网络参数。梯度爆炸则是相反的情况，梯度变得非常大，导致参数更新过大，甚至使网络变得不稳定。
3、目前基于我已知的方法：使用不同的激活函数（如ReLU）、归一化（缩放和平移输入数据或者中间层的激活值）、合适的学习率调度和正则化技术等。
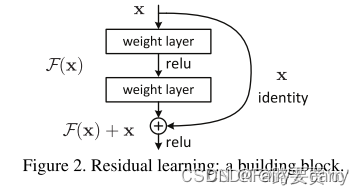
4、因此：本文展示了一种残差学习框架，能够简化使那些非常深的网络的训练，该框架能够将层作为输入学习残差函数，而不是学习未知的函数。
5、结果：残差网络更容易被优化，而且可以在深度增加的情况下让精度也增加。

2.Introduction-介绍

1、主要讲述在深度网络的情况下，首先提出一个问题：训练一个更好的网络是否和堆叠更多的层一样简单呢？
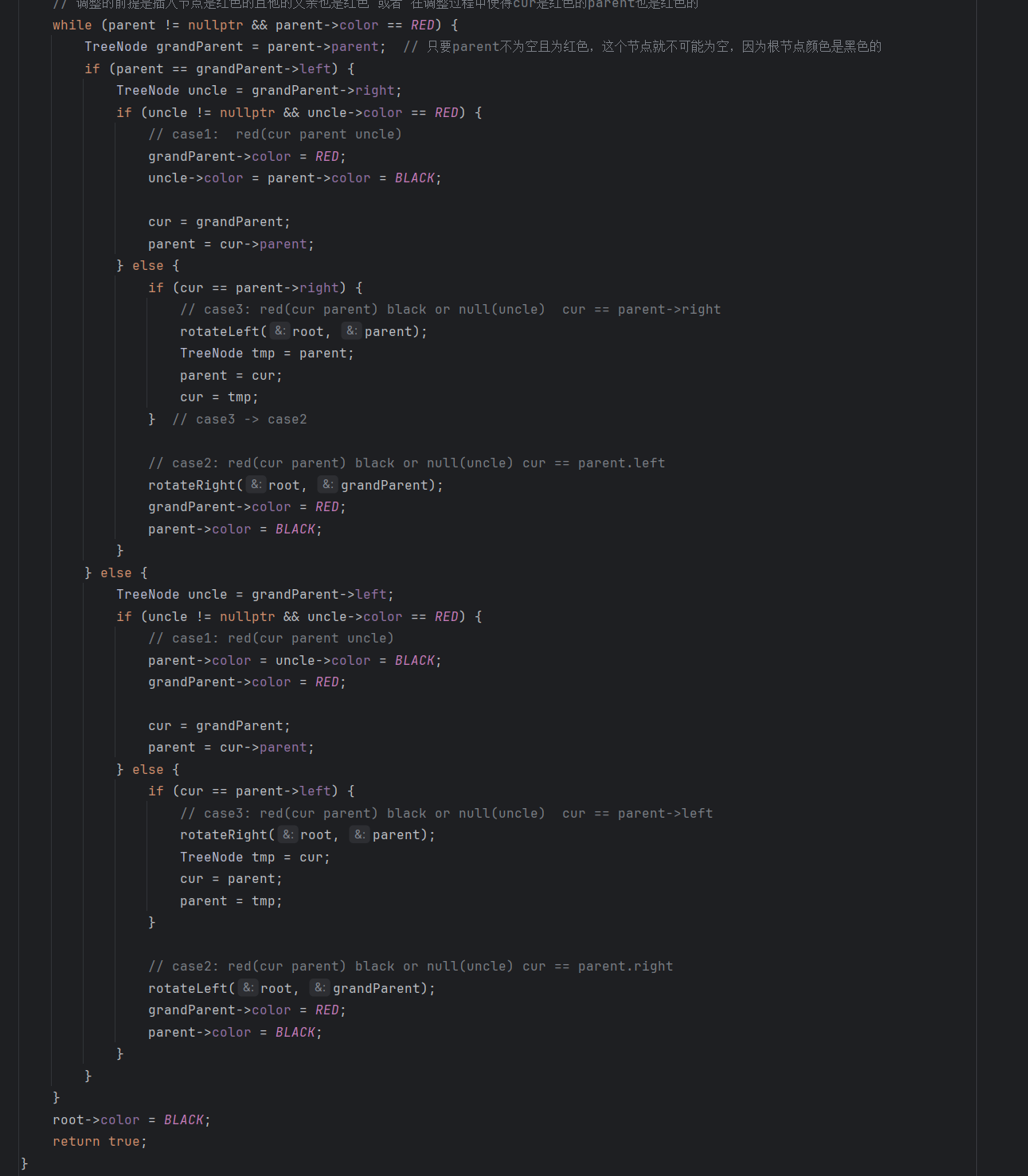
2、但是解决这一个问题的前提：随着网络深度越来越大，梯度消失/梯度爆炸问题随即而来，原因如下：

1.过拟合问题：网络深度越来越大，模型基于训练集的表现能力越来越强（神经网络万能定理：无限个非线性函数能够表示任意复杂的函数），那么此模型可能在测试集上就会出现过拟合问题，过度依赖训练集（类似于考试背答案一样）。
2.激活函数问题：因为我们的梯度是损失函数对参数求偏导，而损失函数（如：MSE）又依赖于我们的激活函数，而梯度的计算是链式计算——>L对w偏导=L对激活函数输出偏导

• 激活函数对输入偏导 …，那么可以发现像sigmoid函数是很容易到0的，故可能出现梯度消失的情况，得不到我们理想的参数。——>(常见处理方法：正则化，Rule，学习率的自适应adam等等)
  3.优化器选择不当： 不同的优化器对深度网络的训练效果有影响。某些优化器可能在处理深度网络时表现更好，而某些优化器可能会导致退化问题。

后来我们的归一化很好的解决了梯度消失/爆炸e的问题（Relu 函数），但是由于非线性激活函数Relu的存在，每次输入到输出的过程都几乎是不可逆的，这也造成了许多不可逆的信息损失。一个特征的一些有用的信息损失了，得到的结果肯定不尽人意。说通俗一点就是中间商赚差价。层数增多之后，信息在中间层损失掉了。

这也就是我们的网络退化问题：即使通过增加网络深度，也并不总能获得更好的训练效果。

3、因此，作者做了一个恒等映射的实验：比较一个浅层模型和一个深层模型时，如果我们将浅层模型中的前几层（即恒等映射）复制到深层模型中，那么这个深层模型的训练错误率不应该高于浅层模型。逻辑如下：

通过复制浅层模型的前几层到深层模型中，使得深层模型的前几层表现和浅层模型相似，保持了一种“相似性”。因此，如果深层模型在训练过程中出现训练错误率更高的情况，那就意味着深层模型的优化出现了问题或者深层模型整体的表现并没有优于浅层模型，这是不符合预期的。

综上所述，个人认为： 作者的重点在于指出当前对于解决深度神经网络训练阶段错误率上升的问题仍然存在挑战，并且目前尚未找到一个有效的方法或解决方案来解决这个问题。

4、作者提出解决方法：深度残差学习 ResNet
（具体方法后续阐述）

5、结论：

1.残差网络的结构更利于优化梯度收敛。
2.解决了退化问题。
3.残差网络可以在扩展网络深度的同时，提高网络性能。

3.Related Work- 相关工作

3.1. Residual Representations—残差表达

1、首先，作者提出了几个base：

1.对于向量量化，残差向量编码比原始向量编码更加有效。
2.Multigrid的残差特性使得求解器比其他标准求解器的收敛要快得多，表明了一个好的重新表达或者预处理能够简化优化问题。

关于第一句话的理解【对于向量量化，残差向量编码比原始向量编码更加有效】： 在原始向量编码中，我们直接将高维向量映射到低维空间中，以便进行存储或传输。这种编码方式可能会丢失一些信息，特别是对于高维数据中的细微差异或结构，而残差向量编码采用了更加巧妙的方法，它首先通过一个基准向量（比如平均值）来表示数据的大致形状或结构，然后将实际数据与基准向量之间的差异（残差）编码到低维空间中。这样做的好处是，在低维空间中，我们可以更有效地表示数据之间的差异，而不必担心丢失整体结构。

关于第二句话的理解【Multigrid的残差特性使得求解器比其他标准求解器的收敛要快得多】： Multigrid算法在处理残差方面的特性使得它比其他常见算法更快地找到问题的解，这也说明了在解决优化问题前，对问题进行有效的重新表达或预处理，可以显著简化问题的解决过程。

1."Multigrid"是一种求解数学问题的算法。
2."残差"是指计算结果与真实结果之间的差异。【这里指的应该是Multigrid算法对数据进行预处理】
3.Multigrid求解器比其他常见的求解器收敛得更快，也就是说，它能更快地找到问题的解。

3.2. Shortcut Connections—短路连接

作用：Shortcut-Connections短路连接是用来帮助信息在深层网络顺利传播的，本身不具备提取特征的作用。

1、首先介绍一下相关概念辅助理清流程：

1.Shortcut连接：在深度神经网络中，shortcut连接是一种将输入直接连接到输出的方式，绕过中间层。它帮助解决深层网络中的一些问题，比如梯度消失和梯度爆炸。

2.多层感知器（MLPs）：这是最基本的神经网络类型，由多个层组成，每层都包含若干个神经元。每个神经元与下一层的所有神经元连接，并通过一个激活函数处理输入。（1.需要大量的计算资源和时间，因为它缺乏卷积和池化操作，无法压缩和提取数据的局部特征；2.MLPs是静态的，对时间序列或序列数据的处理能力有限。3.容易过拟合：如果你的训练数据量不足，MLPs可能会在训练集上表现很好，但在测试集上效果很差。）

3.Inception层：一种特殊的神经网络层设计，包含多个并行的子网络（分支），每个子网络处理不同的特征，然后将结果合并。这种设计能够有效地提取不同尺度的特征。

4.Highway网络（有点像LSTM）：一种改进的深度神经网络结构，使用了门控机制来控制信息的流动。门控机制是数据相关的，并且具有额外的参数，可以选择性地允许信息通过或阻止信息。【每一层有一个“传输门”（transform gate）和一个“携带门”（carry gate），当门的值接近0时，表示信息不会通过该门，也就是说，网络会忽略这一层的输出。这就意味着HIghway网络这一层表示为非残差函数，信息不参与残差计算。】

5.恒等shortcut（Identity Shortcut）：一种特殊的shortcut连接，它直接将输入传递到输出而不进行任何变换。【比如假设有一层使用恒等shortcut连接的网络，输入为 x，输出为 y，网络学习的是残差函数，即y= f(x)+x，其中 f(x)是这一层学习的调整，而我们的恒等shortcut连接确保了 𝑥总是被传递，信息流动顺畅。】

2、举个例子：
想象你在上台阶，普通的网络就像一步一步地走台阶，你可能会觉得很累（直至没力气=梯度消失，且没到终点炸了），中途容易停下来（梯度消失/爆炸）。而shortcut连接就像在每个台阶上都安装了一个电梯，直接让你从一层到达下一层，这样你走得更快、更轻松。

恒等shortcut： 类比中的电梯永远开着，表示输入可以直接传递到输出而不经过任何变换。它的主要作用是让信息在网络中更容易传播，这样在训练过程中，梯度能够更顺利地传递回输入层，从而减轻梯度消失的问题。从而确保信息和梯度在网络中不会削弱。

3、我的想法：

1.在普通的卷积神经网络（CNN）或者VGG（因为VGG主旨不是层数多吗，那就肯定会遇到梯度消失的问题）中加入shortcut连接，帮助信息在网络中流动，减轻梯度消失问题。
2.在某些层中使用Inception层，通过多个并行分支提取不同尺度的特征然后进行合并。
3.Highway网络整合CNN卷积神经网络，Highway层可以嵌入到CNN的卷积层之间，作为卷积层的扩展。这意味着在卷积层之后，可以加一个Highway层，用于决定哪些信息应该被传递到下一层。【例如，在一个具有10个卷积层的CNN中，每个卷积层后面都加一个Highway层。这样，网络能够更深，但训练过程更稳定，效果更好，使得卷积层提取的特征能够更有效地传递到下一层，同时缓解梯度消失问题。】

3.3. Residual Learning—残差学习

1、我们首先翻译一下原文： 我们将H(x)看作一个由部分堆叠的层（并不一定是全部的网络）来拟合的底层映射，其中x是这些层的输入。假设多个非线性层能够逼近复杂的函数，这就等价于这些层能够逼近复杂的残差函数，例如, H(x)−x（假设输入和输出的维度相同）。所以我们明确的让这些层来估计一个残差函数：F(x)=H(x)−x而不是H(x)。因此原始函数变成了：F(x)+x。尽管这两个形式应该都能够逼近所需的函数（正如假设），但是学习的难易程度并不相同。

这段文字的大致意思就是：输入为x，我们的目的是计算原本的输出和输入之间的“残差”，也就是H(x)-x，所以残差函数等于F(x)=H(x)-x
,那么结果就等于H(x)=F(x)+x【输出=差异+输入】，就类似于这就像你走楼梯时有一个电梯（恒等shortcut）帮你省力，你只需要做一些小的调整【学习残差】。

对比以前的方法：
在正常的网络中，应该传递给下一层网络的输入是 H(x)=F(x)，即直接拟合H(x)。

本文的改进：
在ResNet中，传递给下一层的输入变为H(x)=F(x)+x【F(x)为残差】，即拟合残差F(x)=H(x)－x。

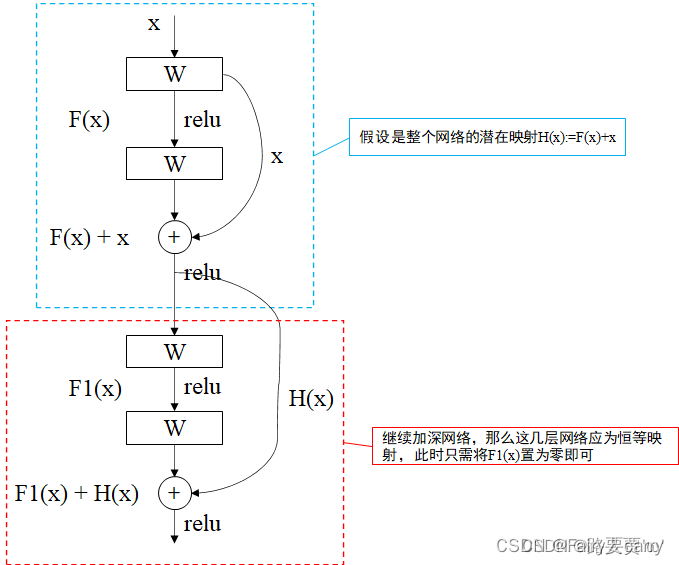
总结：

1、我们加入残差结构后，输入x后就有了一个额外选择，如果说网络学习到当前层的参数是冗余的，我们可以通过恒等shortcut跳过这个冗余层，通过参数调整使得 H(x)=F(x)+x 中的 F(x)恰好等于 0。

2、**恒等映射的好处：**加入恒等映射后，深层网络至少不会比浅层网络表现更差【关键点：保证了深层网络一定不会比浅层网络表现的差】。这是因为即使网络中某些层未能有效学习到有用的特征，它们的输出至少可以直接等于输入，不会破坏已有的信息。

3.4. Identity Mapping by Shortcuts—通过短路连接进行恒等映射

主要讲述的是两个点：恒等映射的两种方式（维度同等与否）

恒等映射：
1、公式：y=F(x，{Wi} ) + x。
F=W2σ(W1x)。
2、F(x，{wi} ) ：表示通过网络层学习的残差映射函数，σ 代表ReLU。
3、这种映射没有额外的参数，计算效率高；它通过 shortcuts 直接传递输入x，不会引入额外的参数也不会增加模块的计算复杂性，因此可以公平地将残差网络和plain网络作比较。

维度匹配：
1、如果输入和输出的维度不同，通过线性变换 𝑊𝑠 将输入 𝑥 映射到相同维度，然后进行相加。这种方式通常在通道数改变时使用。【目的是保持x与F(x)之间的维度一致】
2、公式：y=F(x，{Wi} ) + Ws。

优点：
1、恒等映射能解决深层网络的退化问题，因为它保证了输入信息可以直接传递到输出。
2、在相同条件下，ResNet 的深层网络不会比浅层网络表现更差。

3.5 Network Architectures—网络架构

1、首先我们讲述一下几个必要的概念：

1.1 Plain网络：

plain网络结构主要受VGG网络的启发。 卷积层主要为3*3的卷积核，直接通过stride为2的卷积层来进行下采样。在网络的最后是一个全局的平均pooling层和一个1000类【网络最后的全连接层输出的向量维度为1000，每个维度对应一个类别】的包含softmax的全连接层。加权层的层数为34。

1.简化结构： 与VGG网络相比，Plain网络通常具有更少的层和更少的参数量。它可能使用更少的卷积层或者更小的卷积核大小，以达到简化网络结构的目的。
2.相同特征尺寸的层具有相同数量的滤波器： 这一点与VGG网络类似，为了保持特征图尺寸的一致性，同一层内的滤波器数量通常是相同的。

1.2 残差网络：

残差网络：在plain网络的基础上，加入shortcuts连接，就变成了相应的残差网络。

调整维度的两个方法：

1.zero-padding：对多出来的通道padding补零填充，这种方法不会引入额外的参数；
2.线性投影变换：用1*1卷积升维，是需要学习的参数，精度比zero-padding更好，但是耗时更长，占用更多内存。 这两种方法都使用stride为2的卷积。

三种网络结构的对比：

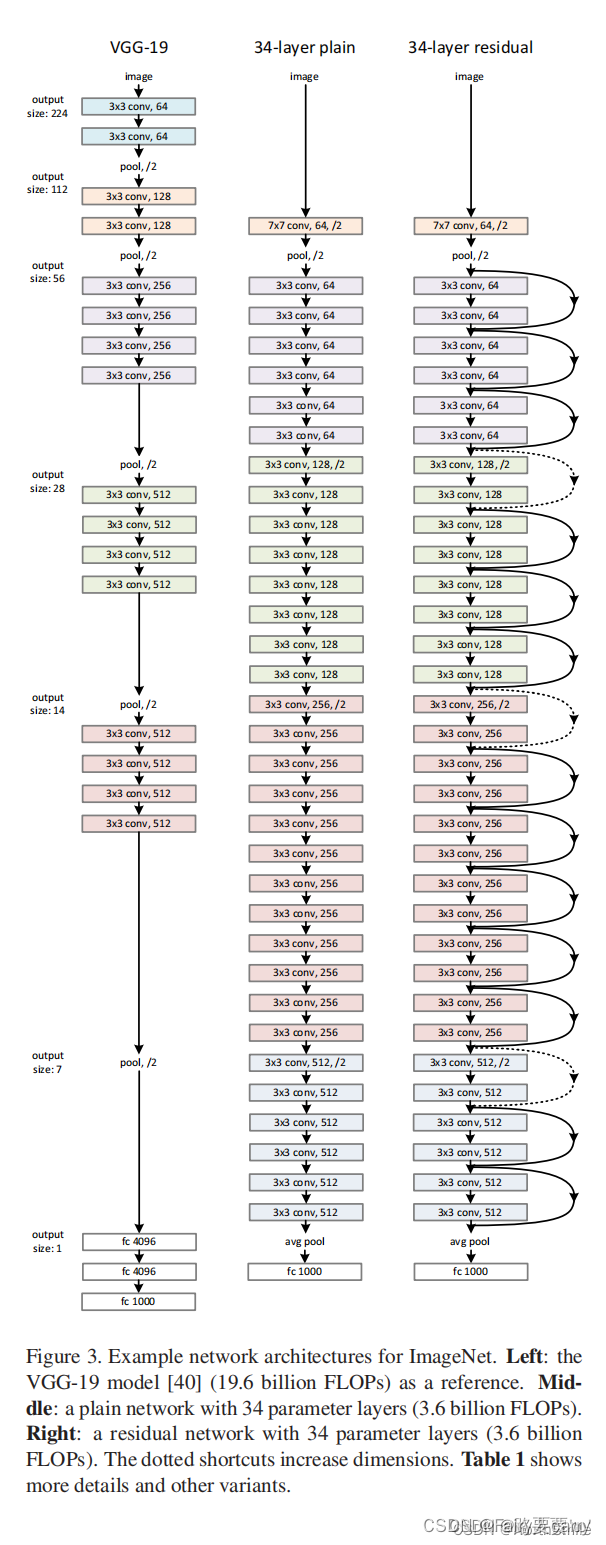
1、首先介绍左边的VGG：

2、然后介绍一下中间的34层plain网络：
介绍： Plain网络通常具有更少的层和更少的参数量。它可能使用更少的卷积层或者更小的卷积核大小，以达到简化网络结构的目的。

3、34层残差网络：

差别：
1、VGG-19：经典的深层卷积网络，通过多层卷积和池化实现特征提取。
2、34层plain：结构简单但存在深层网络训练难度。
3、34层残差：通过残差连接解决深层网络训练中的梯度消失问题，效果更好。

参数和计算量：VGG-19有19.6亿次浮点运算（FLOPs），34层plain和残差网络有3.6亿次FLOPs。
FLOPs 计算的是网络中所有层的所有浮点运算次数的总和，包括卷积运算、矩阵乘法等。对于卷积神经网络（CNN），主要的计算量来自卷积层。
作用： FLOPs 是衡量神经网络计算复杂度和效率的一个重要指标。较高的 FLOPs 通常意味着需要更多的计算资源和时间来训练或推理。