几种流行的并行方法：

• 数据并行（data parallel）
• 模型并行（model parallel）
  • tensor并行
  • pipeline并行
  • sequence并行
• Zero Redundancy Data Parallelism（ZeRO）

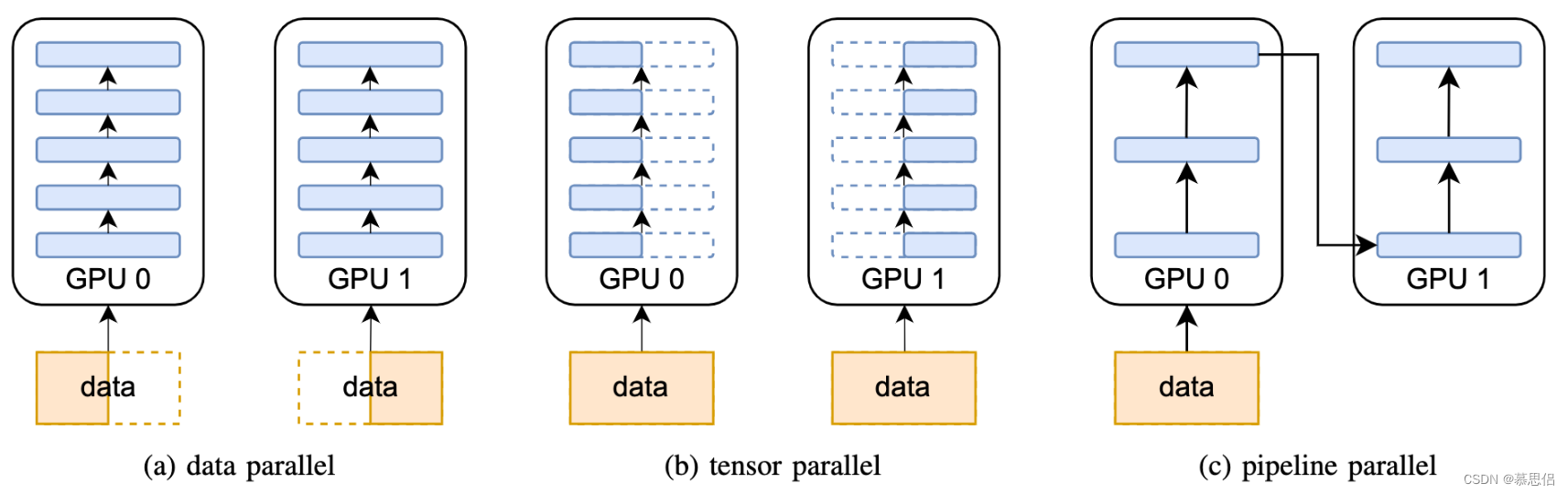
Data parallelism (DP)

经典的数据并行算法是在多个设备上都拷贝一份完整的模型参数，彼此之间可以独立计算，所以每个设备传入的输入数据不一样​，这也是为什么叫数据并行。只不过，每隔一段时间（比如一个batch或者若干个batch）后需要彼此之间同步模型权重的梯度​。随着模型大小不断增大，单个GPU的内存已经无法容纳现如今的大模型，所以便有了后面会介绍的模型并行​。

Model Parallelism (MP)

Pipeline Parallelism (PP)

pipeline parallelism是比较常见的模型并行算法，它是模型做层间划分，即inter-layer parallelism。以下图为例，如果模型原本有6层，你想在2个GPU之间运行pipeline，那么每个GPU只要按照先后顺序存3层模型即可。

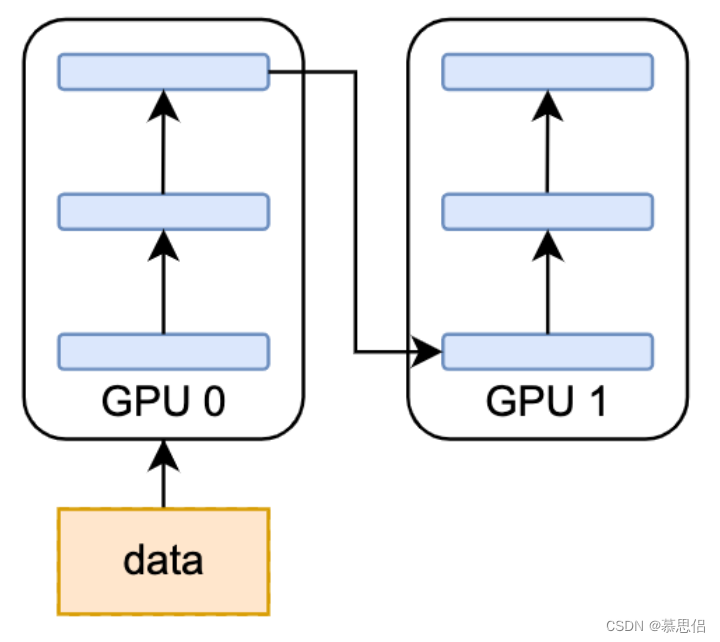
已经有很多Pipeline相关的研究工作了，例如PipeDream，GPipe，和Chimera。它们的主要目的都是降低bubble time。

Tensor Parallelism (TP)

前面介绍的Pipeline Parallelism是对模型层间做划分，叫inter-layer parallelism。那么另一种方式则是对模型层内做划分，即intra-layer Parallelism，也叫Tensor Parallelism。

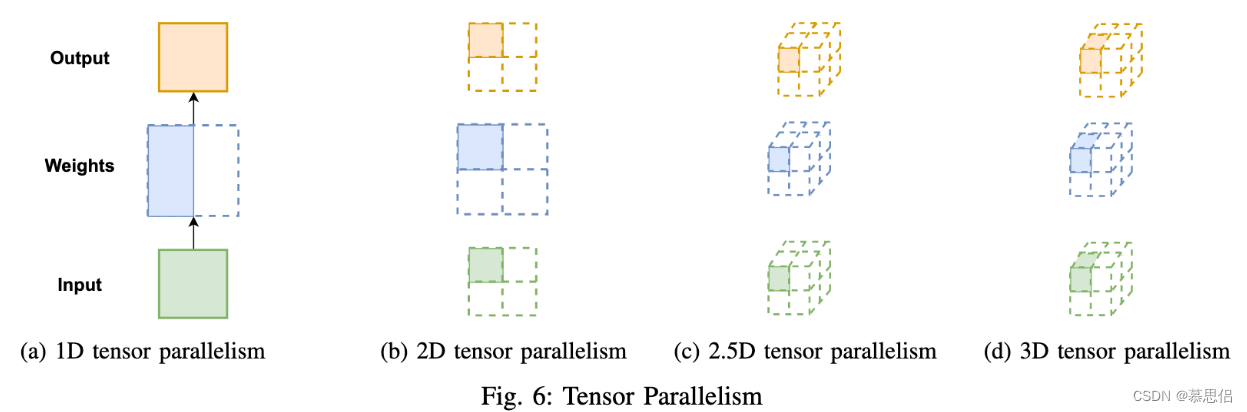
1D Tensor Parallelism

Megatron-LM [1] 是最早提出1D Tensor并行的工作。该工作主要是为了优化transformer训练效率，把线性层按照行或者列维度对权重进行划分。如图4所示，原本线性层为，这里将按列进行划分，将按行进行划分。这样，每个GPU只需要存一半的权重即可，最后通过All-reduce操作来同步Y的结果。当GPU数量为N𝑁时，每个GPU只需要存1N的权重即可，只不过每层输出需要用All-reduce来补全结果之后才能继续下一层的计算。

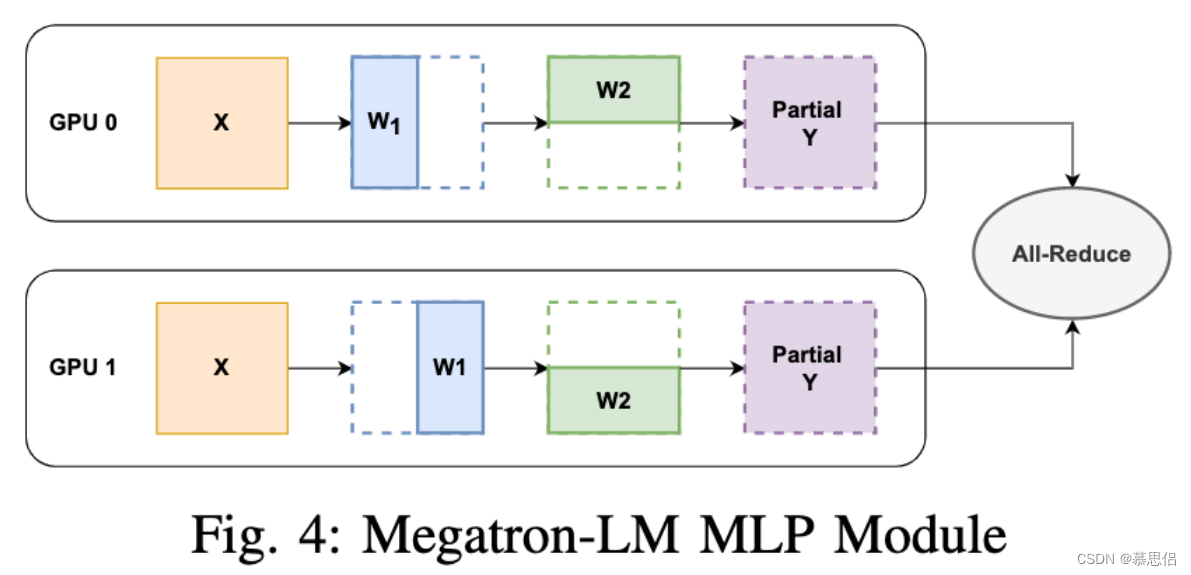
1D Tensor并行对通信速度要求较高，不过1D在每层的输入和输出都有冗余的内存开销。以图4为例，我们可以看到虽然模型权重被划分了，但是每个GPU都有重复的输入X𝑋,另外All-reduce之后每个GPU也会有重复的输出Y𝑌，所以后续一些工作尝试从这里做进一步改进,包括2D, 2.5D,和3D tensor并行。

2D Tensor Parallelism

2D Tensor Parallel [2] 基于SUMMA和Cannon矩阵相乘算法沿着两个不同的维度对 输入数据，模型权重，每层的输出 进行划分。给定N𝑁个GPU，tensor会被划分成N𝑁个chunk（使用torch.chunk），每个GPU保存一个chunk。这N𝑁个GPU呈方形网络拓扑结构，即每行每列均为√N𝑁个GPU。图6b展示了常见的4-GPU的节点划分示意图，假设tensor的维度大小是[P,Q][𝑃,𝑄]，那么划分后每个GPU上存的chunk大小即为[P/√N,Q/√N][𝑃/𝑁,𝑄/𝑁]。至此，每个GPU都只会保存部分的输入输出以及部分的权重。虽然相比于1D Tensor并行，2D额外增加了模型权重的通信，但是需要注意的是当GPU数量很多的时候，每个GPU上分配的模型权重就会小很多，而且因为使用的All-reduce通信方式，所以2D也还是要比1D更高效的。

2.5D Tensor Parallelism

2.5D Tensor Parallel [3] 是受2.5D矩阵乘法算法 [4] 启发进一步对2D Tensor并行的优化。具体来说2.5D增加了 depth 维度。当 depth=1 时等价于2D；当 depth>1 时，

同样假设有N𝑁个GPU，其中N=S2∗D𝑁=𝑆2∗𝐷，S𝑆类似于原来2D正方形拓扑结构的边长，而D𝐷 则是新增加的维度 depth 。D𝐷可以由用户指定，S𝑆 则会自动计算出来了。所以一般来说至少需要8个GPU才能运行2.5D算法，即S=2,D=2𝑆=2,𝐷=2。

3D Tensor Parallelism

3D Tensor Parallel [5] 是基于3D矩阵乘法算法 [6] 实现的。假设有 N𝑁个 GPU，tensor维度大小为[P,Q,K][𝑃,𝑄,𝐾]，那么每个chunk的大小即为 [P/3√N,Q/3√N,K/3√N][𝑃/𝑁3,𝑄/𝑁3,𝐾/𝑁3]。当tensor维度小于3时，以全连接层为例，假设权重维度大小为 [P,Q][𝑃,𝑄] ,那么可以对第一个维度划分两次，即每个chunk的维度大小为 [P/(3√N)2,Q/3√N][𝑃/(𝑁3)2,𝑄/𝑁3] 。3D Tensor并行的通信开销复杂度是 O(N1/3)𝑂(𝑁1/3) ，计算和内存开销都均摊在所有GPU上。

小结

1D Tensor并行每一层的输出是不完整的，所以在传入下一层之前都需要做一次All-gather操作，从而使得每个GPU都有完整的输入，如图7a所示。

2D/2.5D/3D Tensor 并行算法因为在一开始就对输入进行了划分， 所以中间层不需要做通信，只需要在最后做一次通信即可。在扩展到大量设备（如GPU）时，通信开销可以降到很小。这3个改进的Tensor并行算法可以很好地和Pipeline并行方法兼容。

Zero Redundancy Data Parallelism (ZeRO)

训练过程中GPU内存开销主要包含以下几个方面：

• 模型状态内存（Model State Memory）：
  • 梯度
  • 模型参数
  • 优化器状态：当使用像Adam这样的优化器时，优化器的状态会成为GPU内存开销的大头。前面介绍的DP，TP， PP算法并没有考虑这个问题。
• 激活内存（Activation Memory）：在优化了模型状态内存之后，人们发现激活函数也会导致瓶颈。激活函数计算位于前向传播之中，用于支持后向传播。
• 碎片内存（Fragmented Memory）：深度学习模型的低效有时是由于内存碎片所导致的。在模型之中，每个张量的生命周期不同，由于不同张量寿命的变化而会导致一些内存碎片。由于这些碎片的存在，会导致即使有足够的可用内存，也会因为缺少连续内存而使得内存分配失败。ZeRO 根据张量的不同寿命主动管理内存，防止内存碎片。

ZeRO针对模型状态的三部分都做了对应的内存改进方法：

• ZeRO1：只划分优化器状态(optimizer states, os)，即Pos
• ZeRO2：划分优化器状态和梯度(gradient, g)，即Pos+g
• ZeRO3：划分优化器状态和梯度和模型参数(parameters, p)，即Pos+g+p

下图给出了三种方法带来的内存开销收益

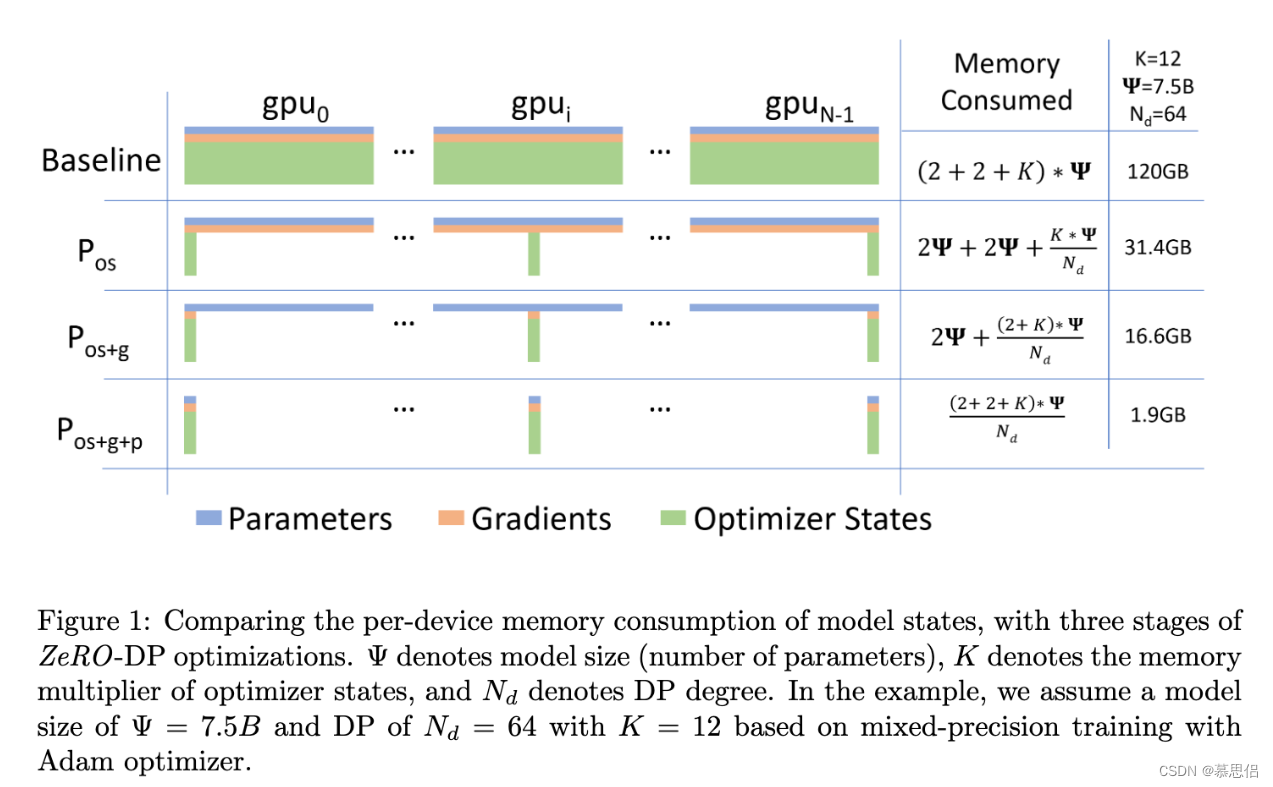
不管采用三种方法的哪一种，ZeRO简单理解就是给定N𝑁个设备，然后把一堆data等分到这些设备上，每个设备只存1/N1/𝑁的数据量，并且每次也只负责更新这1/N1/𝑁的数据。

因为对数据做了划分，ZeRO在每一层都需要有通信操作。我们考虑ZeRO在某一层的具体操作：

• 在forward的时候，会首先使用all-gather让每个设备拥有该层完整的模型权重，然后计算得到输出，最后每个设备会只保留原来的权重，即把all-gather过来的权重扔掉，这样可以节省开销。
• 在backward的时候，同样会先all-gather该层的所有权重，然后计算梯度，最后也会把梯度进行划分，每个设备上只会存1/N对应的梯度数据。

注意ZeRO对数据划分方式并没有什么具体的要求，可以是随意划分，因为最后反正会用all-gather使得所有设备商都有用完整的数据；当然，也可以使用前面提到的Tensor Parallelism的划分方式，这样一来可以有效降低通信开销，进一步提高效率。

参考链接：https://www.cnblogs.com/marsggbo/p/16871789.html