- 深入理解SVM和浅层机器学习算法的训练机制
- 支持向量机(SVM)的训练过程
- SVM的基本概念
- SVM的损失函数
- 训练方法
- 浅层机器学习算法的训练机制
- 决策树
- K-最近邻(K-NN)
- 朴素贝叶斯
- 结论
深入理解SVM和浅层机器学习算法的训练机制
在探讨浅层机器学习算法时,支持向量机(SVM)是一个经典且强大的例子。这种算法的训练机制、是否需要损失函数,以及与其他浅层机器学习算法的比较,是理解浅层学习方法的关键。本篇博客将详细解释SVM的训练过程、损失函数的角色,并阐述其他浅层机器学习算法的训练方式。
支持向量机(SVM)的训练过程
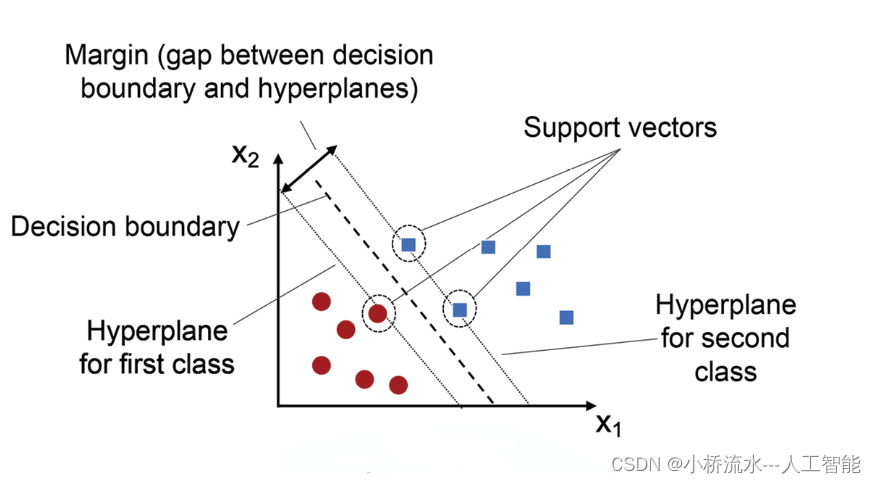
SVM的基本概念
支持向量机(SVM)是一种有效的分类技术,它在高维空间中寻找最佳的分割超平面,以区分不同类别的数据点。这种方法的目的是最大化分类边界的间隔,从而提高分类的准确性和模型的泛化能力。
SVM的损失函数
SVM的训练确实涉及到一个损失函数,通常是 铰链损失函数(Hinge Loss)。这个损失函数是为了实现“最大间隔”而设计的。在数学上,对于线性SVM,损失函数可以表达为:
L = ∑ i = 1 n max ( 0 , 1 − y i ( w ⋅ x i + b ) ) + λ ∥ w ∥ 2 L = \sum_{i=1}^{n} \max(0, 1 - y_i(w \cdot x_i + b)) + \lambda \|w\|^2 L=i=1∑nmax(0,1−yi(w⋅xi+b))+λ∥w∥2
其中, x i x_i xi 是数据点, y i y_i yi 是每个点的标签,( w ) 是超平面的法向量,( b ) 是偏置项,而 λ ∥ w ∥ 2 \lambda \|w\|^2 λ∥w∥2是正则化项,用来防止模型过拟合。
训练方法
SVM的训练过程涉及优化上述损失函数,通常使用二次规划、梯度下降或者更专门的优化算法(如序列最小优化SMO算法)。这些方法能够有效地调整 ( w ) 和 ( b ),以最小化损失函数,实现最大间隔。
浅层机器学习算法的训练机制
浅层机器学习算法是一个广泛的类别,包括决策树、K-最近邻(K-NN)、朴素贝叶斯等,它们的训练机制各不相同。
决策树
决策树通过递归地分割数据来构建树结构。它不需要传统意义上的损失函数,而是依据信息增益或基尼不纯度来选择分割的属性。
K-最近邻(K-NN)
K-NN实际上并不进行显式的训练过程。它在分类时,简单地根据距离度量在训练数据中查找最近的K个邻居,并基于这些邻居的标签来预测新数据点的类别。
朴素贝叶斯
朴素贝叶斯基于概率模型,它通过计算特征的条件概率来进行分类。这一过程涉及到统计训练数据中各类特征的频率,但不涉及损失函数。
结论
尽管不是所有的浅层机器学习算法都需要损失函数,但对于像支持向量机这样的一些算法,损失函数是它们训练过程中不可或缺的一部分。了解这些算法是否需要损失函数及其训练过程的细节,对于有效地应用这些算法至关重要。希望本篇博客能够帮助您深入理解不同浅层机器学习算法的训练机制,并在实际应用中做出更合适的选择。



![[HDCTF 2023]爬过小山去看云(HILL密码,云影密码)](https://img-blog.csdnimg.cn/direct/6d36c07c411a416280309f124d8ed3a2.png)