左极限与右极限
1. 前言
极限描述了函数在一个定点附近的行为,具体说就是当函数的自变量(例如 x x x)趋近于某一个值时,函数的因变量(例如 y y y)会产生什么样的特性(或结果)。
2. 方向
我们知道在函数坐标轴(正交坐标轴)可以表示出函数包含的每一个点(即每一个 x x x 以及对应的 y y y 值),沿着这些点就可以绘制出函数的图像。函数坐标轴根据函数的 x x x 和 y y y 的符号,定义了四个象限,这四个象限完全可以表示出函数包含的所有特征,所以函数坐标轴具有明确的符号方向性。
既然函数坐标轴具有方向性,所以极限在描述函数在一个定点附近的行为时,有两种方式去逼近这个定点的附近,即从定点的左侧或从定点的右侧去逼近该定点。
3. 实例
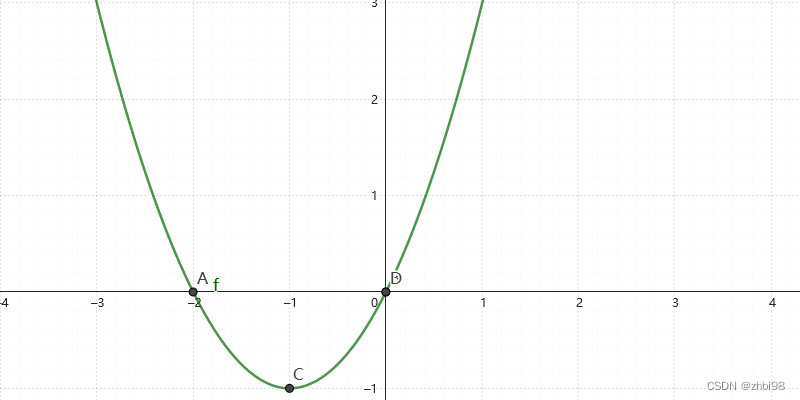
这里以一个爬山的形象例子来抽象的描述极限的方向性问题,我们可以将山谷的轮廓看作函数曲线,山谷的高度看作函数值,行人的运动看作逐渐逼近定点的过程。并且我们根据山谷的水平位置和高度将山谷的曲线设定为函数 h ( x ) h(x) h(x)。因此问题转化为了 h ( x ) h(x) h(x) 在 x = 3 x=3 x=3 附近的行为。
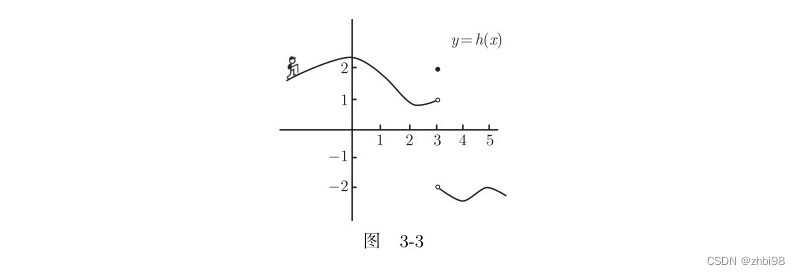
描述图中的行人,当行人从左侧接近于 x = 3 x=3 x=3 时会发生什么呢?想象一下,顺着山势上下, h ( x ) h(x) h(x) 会告诉你, 当你的水平位置是 x x x 时, 行人所在高度是多少。因此,如果行人从图的左边向右走,那么当行人的水平位置接近于 3 3 3 时, 行人所在高度就会接近于 1 1 1。
但是可以看见图中包含一个 x = 3 x=3 x=3 时 h ( x ) = 2 h(x)=2 h(x)=2 的点,但是要注意 x = 3 x=3 x=3 时 h ( x ) = 2 h(x)=2 h(x)=2 是 x x x 完全等于 3 3 3 时的值,所以这实际上是一个分段函数,不仅如此, 当到达 x = 3 x=3 x=3 时行人高度还会陡然坠落。
x = 3 x=3 x=3 并不在函数的 定义域 中,就趋于极限的行为而言,极限只能无限靠近于 3 3 3 不可能完全等于 3 3 3,所以 h ( 3 ) = 2 h(3)=2 h(3)=2 实际上是无关紧要的,并不会影响极限的值。至于 x = 3 x=3 x=3 时行人高度还会陡然坠落,这是在 x = 3 x=3 x=3 以及 x = 3 x=3 x=3 右侧的值,我们暂时先不关心(无关紧要)。
左极限:因此,就可以看到函数 h ( x ) h(x) h(x) 在 x = 3 x=3 x=3 的 左极限 等于 1 1 1。
右极限:另一方面,如果行人从图的右边向左走,那么当行人的水平位置无限接近于 x = 3 x=3 x=3 时,行人所在高度就会接近于 − 2 −2 −2。这就是说函数 h ( x ) h(x) h(x) 在 x = 3 x=3 x=3 的 右极限 等于 − 2 −2 −2。同样这时任何在 x = 3 x=3 x=3 以及左侧 (包含 x = 3 x=3 x=3 本身) 的值都是无关紧要的。
4. 符号表示
可将上述发现的左极限和右极限通过符号的方式总结如下,其中第一个极限式子中
3
3
3 后的小减号 - 表示该极限是一个左极限,第二个极限式子中
3
3
3 后的小加号 + 表示该极限是一个右极限:
lim x → 3 − h ( x ) = 1 以及 lim x → 3 + h ( x ) = − 2 \lim_{x \rightarrow 3−}h(x)=1 \ \ 以及 \ \ \lim_{x \rightarrow 3+} h(x)=−2 x→3−limh(x)=1 以及 x→3+limh(x)=−2
在 3 3 3 的后面写上减号或加号,而不是在前面,这是非常重要的!例如,如果你写成 lim x → − 3 h ( x ) \lim_{x→−3} h(x) limx→−3h(x),那么指的是 h ( x ) h(x) h(x) 在 x = − 3 x=−3 x=−3 时的通常的双侧极限,而不是 h ( x ) h(x) h(x) 在 x = 3 x=3 x=3 时的左极限,这确实是两个完全不同的概念。
在左极限的极限符号底下写 x → 3 − x → 3− x→3− 的理由是, 此极限只涉及小于 3 3 3 的 x x x 的值,也就是说,你需要在 3 3 3 上减一点点来看会有什么情况发生,类似地, 对于右极限,当你写 x → 3 + x → 3+ x→3+ 的时候,这意味着你只需要考虑如果在 3 3 3 上加一点点会有什么情况发生。
5. 双侧极限
通常的双侧极限在 x = a x=a x=a 处存在,不过仅当左极限和右极限在 x = a x=a x=a 处都存在且两者相等的条件下才能成立。 在这种情况下,这三个极限(双侧极限,左极限和右极限)都是一样的,用数学的语言描述,如下:
lim x → a − f ( x ) = L 且 lim x → a + f ( x ) = L \lim_{x\rightarrow a−}f(x)=L \ \ 且 \ \ \lim_{x \rightarrow a+}f(x)=L x→a−limf(x)=L 且 x→a+limf(x)=L
左极限喝右极限相等时,合称极限,所以如果说极限存在指的是左极限和右极限都存在且相等,表达式等价于
lim x → a f ( x ) = L \lim_{x \rightarrow a}f(x)=L x→alimf(x)=L
如果左极限和右极限不相等,例如上述例子中的函数
h
(
x
)
h(x)
h(x),那么双侧极限不存在,我们写作如下,或使用缩写 DNE 表示 “不存在”。
lim x → 3 h ( x ) 不存在 \lim_{x \rightarrow 3}h(x) \ \ 不存在 x→3limh(x) 不存在
6. 总结
(1) 双侧极限在函数连续性判断方面具有重要的作用,需要重点记忆双侧极限和函数连续性的关系,后续会重点讲解。
(2) 从本次的左右极限相关的内容也可以知道函数的定义域对极限具有一定的影响,后续会重点讲解。
(3) 极限存在的充分必要条件是左极限和右极限都存在且相等,在分段函数方面尤其需要注意,很容易出现左极限和右极限不相等的情况。