本模型是解决一个十分类的问题:
在这之前,可以先看看一个Pytorch的简单的示例:
它展示了如何定义一个简单的神经网络、准备数据、训练模型以及评估模型:
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
# 假设我们有一些简单的输入输出数据
x_data = torch.tensor([[1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0]])
# 定义一个简单的线性模型
class LinearRegressionModel(nn.Module):
def __init__(self):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(1, 1) # 输入特征数为1,输出特征数也为1
def forward(self, x):
y_pred = self.linear(x)
return y_pred
model = LinearRegressionModel()
# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 将数据包装为 PyTorch 的 DataLoader
dataset = TensorDataset(x_data, y_data)
data_loader = DataLoader(dataset, batch_size=1, shuffle=True)
# 训练模型
for epoch in range(100):
for i, (inputs, targets) in enumerate(data_loader):
# 前向传播
outputs = model(inputs)
loss = criterion(outputs, targets)
# 反向传播和优化
optimizer.zero_grad() # 清除之前的梯度
loss.backward() # 反向传播计算梯度
optimizer.step() # 更新权重
if (epoch+1) % 10 == 0:
print(f'Epoch [{epoch+1}/{100}], Loss: {loss.item():.4f}')
# 评估模型(这里简单地打印最后一个预测结果)
with torch.no_grad(): # 不需要计算梯度
predictions = model(x_data)
print(f'Predictions: {predictions.data}')
定义了一个简单的线性回归模型,并使用均方误差(MSE)作为损失函数。
使用了随机梯度下降(SGD)优化器来更新模型的权重。
数据被包装为 PyTorch 的 DataLoader,它使得批量处理和数据打乱变得简单。
最后,在训练过程中打印了每个 epoch 的损失,并在训练结束后打印了模型的预测结果。
现在正式进行!!!
实现了一个简单的多层感知器(Multi-Layer Perceptron, MLP)模型来对 MNIST 数据集中的手写数字进行分类。主要包括以下内容:
-
定义了一个名为
Model的继承自nn.Module的模型类,其中包括三个全连接层:liner_1、liner_2和liner_3,并在forward方法中实现了前向传播逻辑。 -
使用
torchvision加载 MNIST 数据集,并对数据进行处理。 -
创建了训练数据加载器
train_dl和测试数据加载器test_dl,以及模型和优化器的初始化。 -
定义了
train函数用于训练模型,并且在训练过程中计算损失和精度。 -
定义了
test函数用于测试模型的效果。 -
对模型进行了多轮(50 轮)的训练和测试,并在每个 epoch 结束后输出当前 epoch 的损失和准确率。最后输出 “Done!!!” 表示训练完成。
-
使用 matplotlib 对训练过程中的损失和正确率进行可视化展示。
下面通过绘图来看一下MNIST数据集中的这些图片是什么样子的。使用Matplotlib库绘图,绘制imgs中的前10张图片:

创建一个简单的多层感知器,这个模型使用torch.nn.Linear层创建。
torch.nn.Linear层是全连接层,本质上就是对全部输入加权求和,它要求输入数据集的形状为一维的,如果使用批量运算,则增加一个batch维,也就是需要输入数据是二维的形状,第一维是batch维,第二维是数据特征,即(batch_size,feature_length)形式。
将训练和测试数据、优化器、损失函数和模型等全部准备好了,再编写训练循环。为了方便以后代码复用,我们将编写一个训练函数train()和一个测试函数test(),在这两个函数中分别对全部训练数据和全部测试数据进行一次训练或测试。
train()函数中,首先使用len(dataloader.dataset)获取训练数据集样本总数量,使用len(dataloader)获取当前dataloader总批次数;然后对传进来的训练数据dataloader进行迭代,在迭代过程中,首先调用模型对当前批次的输入进行预测,并根据真实标签y计算一个批次中样本的平均损失;然后使用反向传播算法,根据损失优化模型参数;最后为了方便了解模型随着训练在数据集上的损失和正确率变化情况,初始化一个correct变量,并用它累计所有批次中预测正确的样本总数;初始化一个train_loss变量,用于累计所有批次的损失之和,这里的train_loss是所有批次的损失之和,所以计算全部样本的平均损失时需要除以总批次数,correct是预测正确的样本总数,计算整个epoch总体正确率,需要除以样本总数量。至此就得到了训练中平均正确率和平均损失值。
test()函数代码与train()函数类似,不过在test()函数代码中,仅仅测试模型在测试数据集的表现,也就是计算模型在测试数据集上的正确率和损失,并没有使用反向传播算法根据损失优化模型参数等部分的代码
所需的完整代码如下:(可运行)
import matplotlib.pyplot as plt
import torchvision
from torchvision.transforms import ToTensor
from torch import nn
class Model(nn.Module):
def __init__(self):
super().__init__()
# 第一层输入展平后的特征长度为28×28,创建120个神经元
self.linear_1 = nn.Linear(28×28,120)
# 第二层输入的是前一层的输出,创建84个神经元
self.linear_2 = nn.Linear(120,84)
# 输出层接收第二层的输入84,输出分类个数10
self.linear_3 = nn.Linear(84,10)
def forward(self, input):
# 将输入展平为2维
x = input.view(-1,28*28)
# 连接第一层linear_1,并使用ReLU函数激活
x = torch.relu(self.linear_1(x))
# 连接第二层linear_2,并使用ReLU函数激活
x = torch.relu(self.linear_2(x))
# 输出层,输出张量的长度,与类别数量一致
x = self.linear_3(x)
return x
train_ds = torchvision.datasets.MNIST('data/', train=True, download=True, transform=ToTensor())
test_ds = torchvision.datasets.MNIST('data/', train=False, download=True, transform=ToTensor())
train_dl = torch.utils.data.DataLoader(train_ds, batch_size=64,shuffle=True)
test_dl = torch.utils.data.DataLoader(test_ds, batch_size=46)
imgs, labels = next(iter(train_dl))
print(imgs.shape)
print(labels.shape)
# 创建画布
plt.figure(figsize=(10,1))
for i,img in enumerate(imgs[:10]):
# 将张量转化为ndarray
npimg = img.numpy()
# 将图形形状由(1,28,28)转为(28,28)
npimg = np.squeeze(npimg)
# 初始化子图
plt.subplot(1,10,i+1)
plt.imshow(npimg)
# 关闭显示子图坐标
plt.axis('off')
# 首先获取当前环境可用的训练设备(CPU或GPU),然后初始化前面编写的多层感知器模型,并在初始化模型后设置模型使用当前可用的device
device = "cuda" if torch.cuda.is_available() else "cpu"
print("Using {} device".format(device))
model = Model().to(device) # 初始化模型,并设置模型使用device
# 初始化交叉熵损失函数
loss_fn = nn.CrossEntropyLoss()
# 初始化优化器 随机梯度下降优化器
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)
def train(dataloader,model,loss_fn,optimizer):
size = len(dataloader.dataset) # 获取当前数据集样本的总数量
num_batches = len(dataloader) # 获取当前dataloader 总批次数
# train_loss 用于累计所有批次的损失之和,correct 用于累计预测正确的样本总数
train_loss ,correct = 0,0
for X,y in dataloader: # 对dataloader进行迭代
X,y = X.to(device),y.to(device) # 每一批次的数据设置为使用当前device
# 进行预测,并计算一个批次的损失
pred = model(X)
loss = loss_fn(pred,y) # 返回的是平均损失
# 使用反向传播算法, 根据损失优化模型参数
optimizer.zero_grad() # 将模型参数的梯度全部归零
loss.backward() # 损失反向传播,计算模型参数梯度
optimizer.step() # 根据梯度优化参数
with torch.no_grad():
correct += (pred.argmax(dim=1) == y).type(torch.float).sum().item()
train_loss += loss.item()
# 由于train_loss 是所有批次的损失之和,所以计算全部样本的平均损失时需要除以总批次数
train_loss /= num_batches
# correct 是预测正确的样本总数,若计算整个epoch总体正确率,需除以样本总数量
correct = correct / size
return train_loss,correct
def test(dataloader,model):
size = len(dataloader.dataset)
num_batches = len(dataloader)
test_loss ,correct = 0,0
with torch.no_grad():
for X,y in dataloader:
X,y = X.to(device),y.to(device)
pred = model(X)
test_loss += loss_fn(pred,y).item()
correct += (pred.argmax(dim=1) == y).type(torch.float).sum().item()
test_loss /= num_batches
correct = correct / size
return test_loss,correct
epochs = 50 # 一个epoch 代表对全部数据训练一遍
train_loss = [] # 每个epoch训练中训练数据集的平均损失被添加到此列表
train_acc = [] # 每个epoch训练中训练数据集的平均正确率被添加到此列表
test_loss = [] # 每个epoch训练中测试数据集的平均损失被添加到此列表
test_acc = [] # 每个epoch训练中测试数据集的平均正确率被添加到此列表
for epoch in range(epochs):
# 调用 train() 函数训练
epoch_loss ,epoch_acc =train(train_dl,model,loss_fn,optimizer)
# 调用 test() 函数测试
epoch_test_loss,epoch_test_acc = test(test_dl,model)
train_loss.append(epoch_loss)
train_acc.append(epoch_acc)
test_loss.append(epoch_test_loss)
test_acc.append(epoch_test_acc)
# 定义一个打印的模板
template = ("epoch:{:2d},train_loss:{:.5f},train_acc:{:.1f},test_loss:{:.5f},test_acc:{:.1f}%")
print(template.format(epoch,epoch_loss,epoch_acc*100,epoch_test_loss,epoch_test_acc*100))
print("Done!!!")
# 可视化直观展示
# 训练过程中损失的变化情况绘图
plt.plot(range(1, epochs+1), train_loss, label='train_loss')
plt.plot(range(1, epochs+1), test_loss, label='test_loss', ls="--")
plt.xlabel('epoch')
plt.legend()
plt.show()
# 正确率变化曲线绘图
plt.plot(range(1, epochs+1), train_acc, label='train_acc')
plt.plot(range(1, epochs+1), test_acc, label='test_acc', ls="--")
plt.xlabel('epoch')
plt.legend()
plt.show()
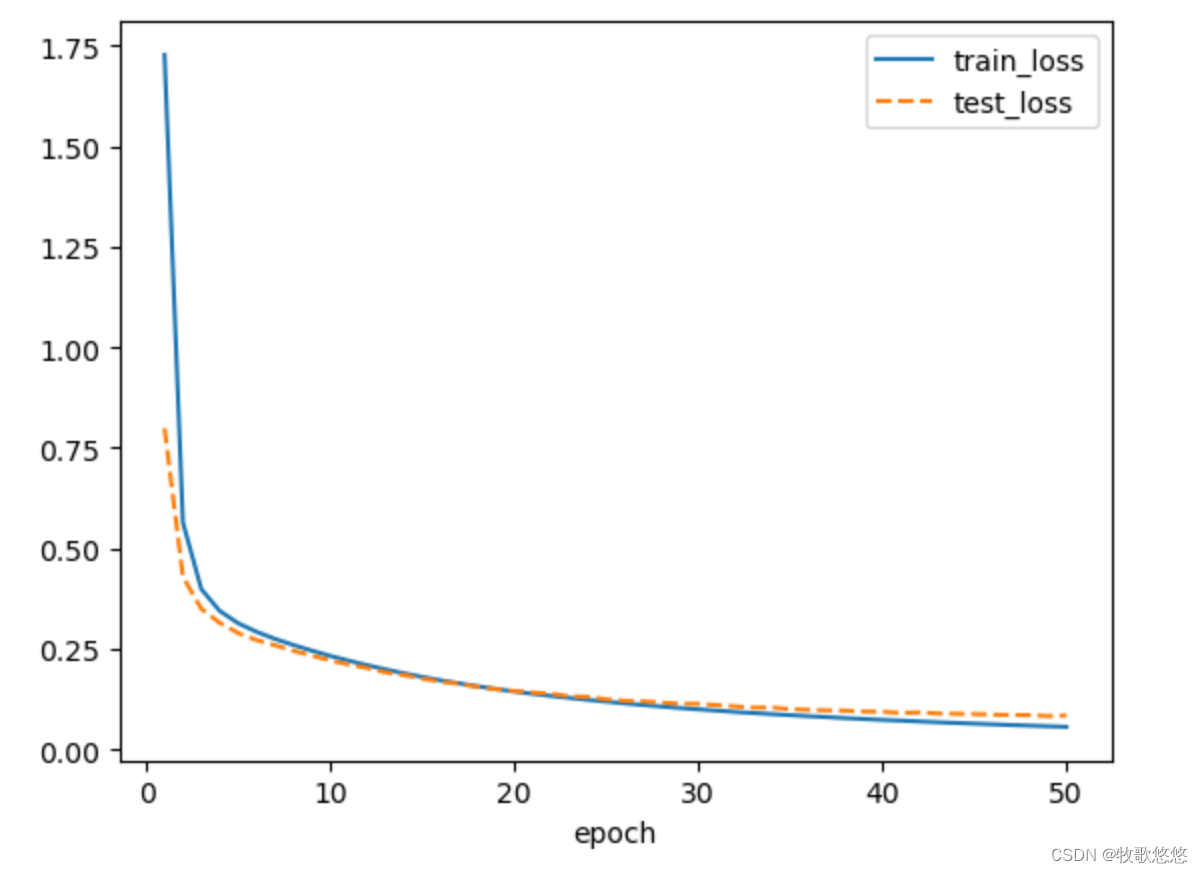
随着训练epoch数量的增加,刚开始时损失在快速下降,到后面时损失曲线越来越平,下降速度变慢;正确率也有类似的特点,随着epoch增加,正确率的曲线也接近水平,说明模型训练已经接近饱和,继续训练不能更好地优化模型,此时我们可以停止训练











![[随笔] 在CSDN的6周年纪念日随笔](https://img-blog.csdnimg.cn/direct/e9c556e4b70145d19e3e5d29c05b074b.png)