文章目录
- 八、排序
- 1.插入排序
- 1.1 直接插入排序
- 1.2 折半插入排序
- 1.3 希尔排序
- 2.交换排序
- 2.1 冒泡排序
- 2.2 快速排序
- 3.选择排序
- 3.1 简单选择排序
- 3.2 堆
- 3.2.1 堆排序
- 3.2.2 堆插入删除
- *完善代码 堆
- 4.归并、基数、计数排序
- 4.1 归并排序
- 4.2 基数排序
- 4.3 计数排序
- 5.内部排序算法的比较
- *完整代码 排序
八、排序
1.插入排序
1.1 直接插入排序
-
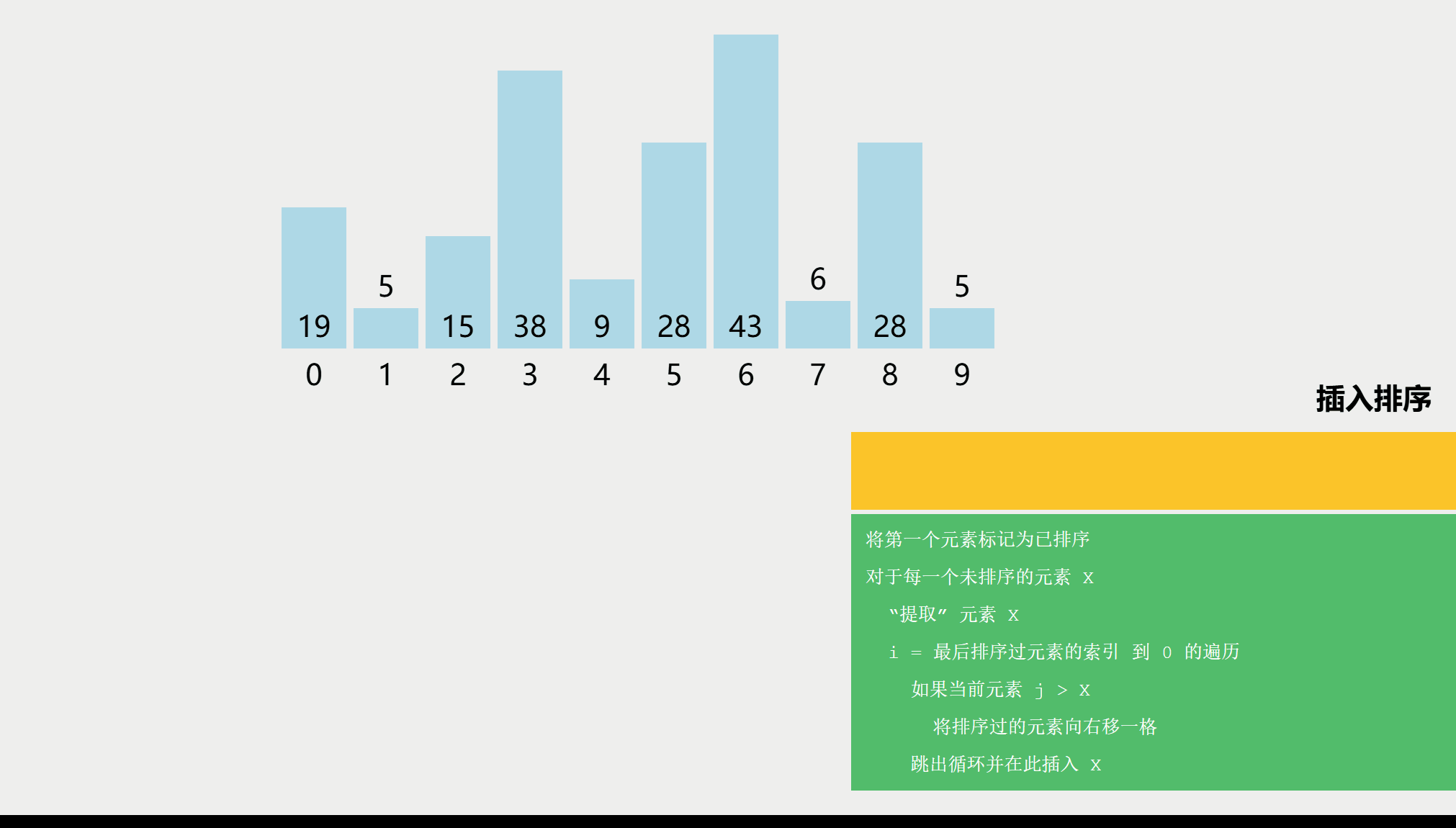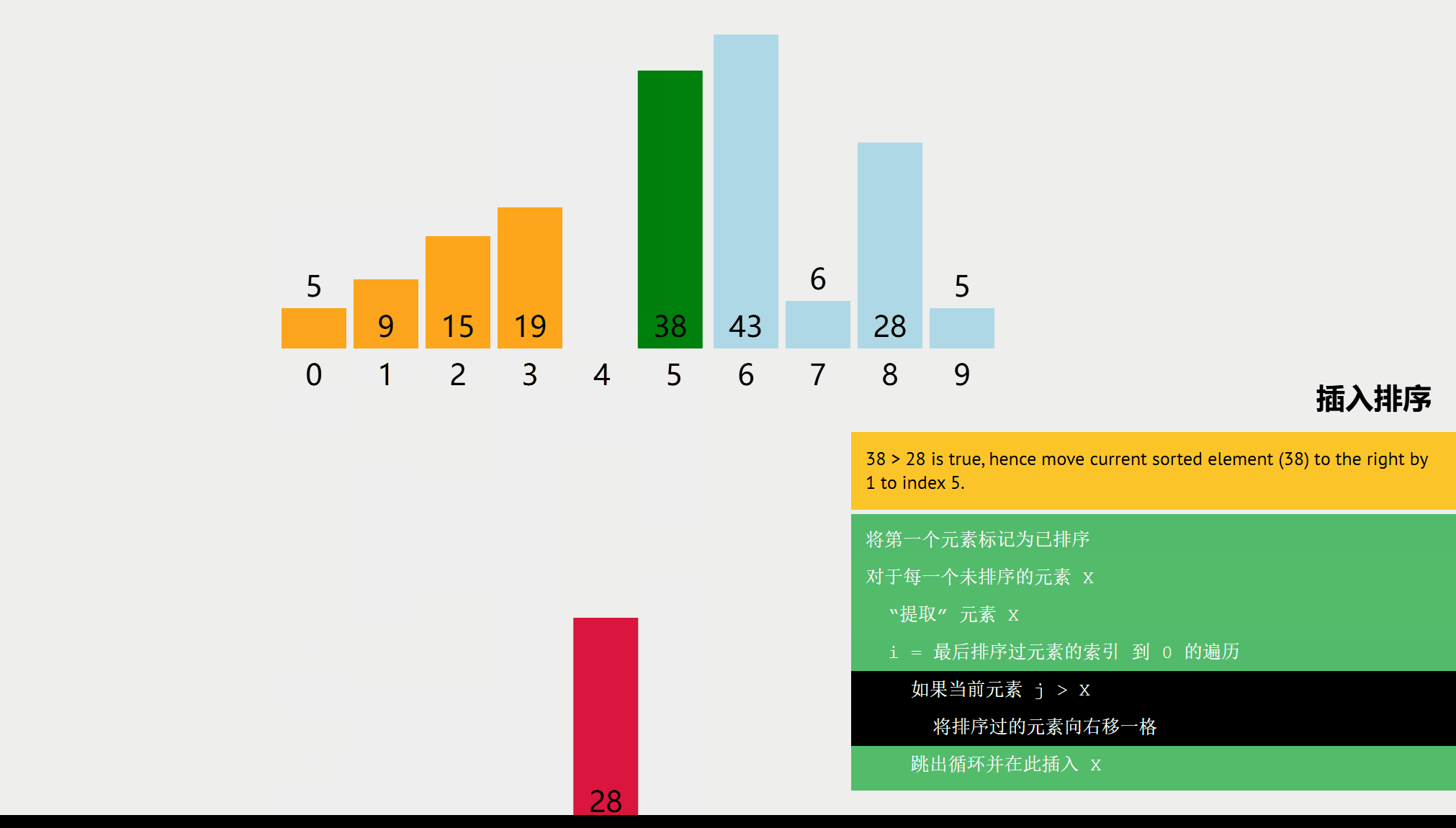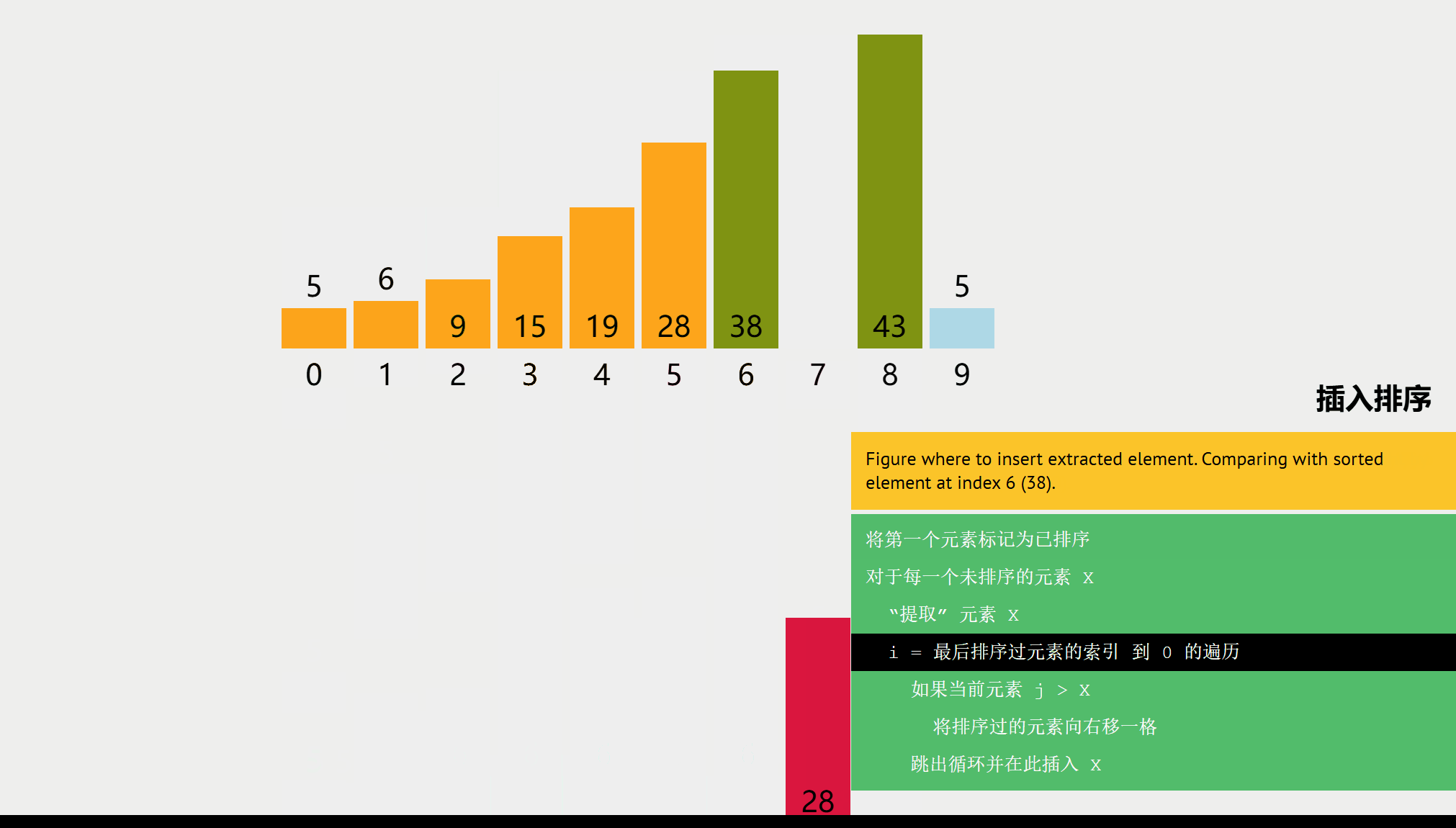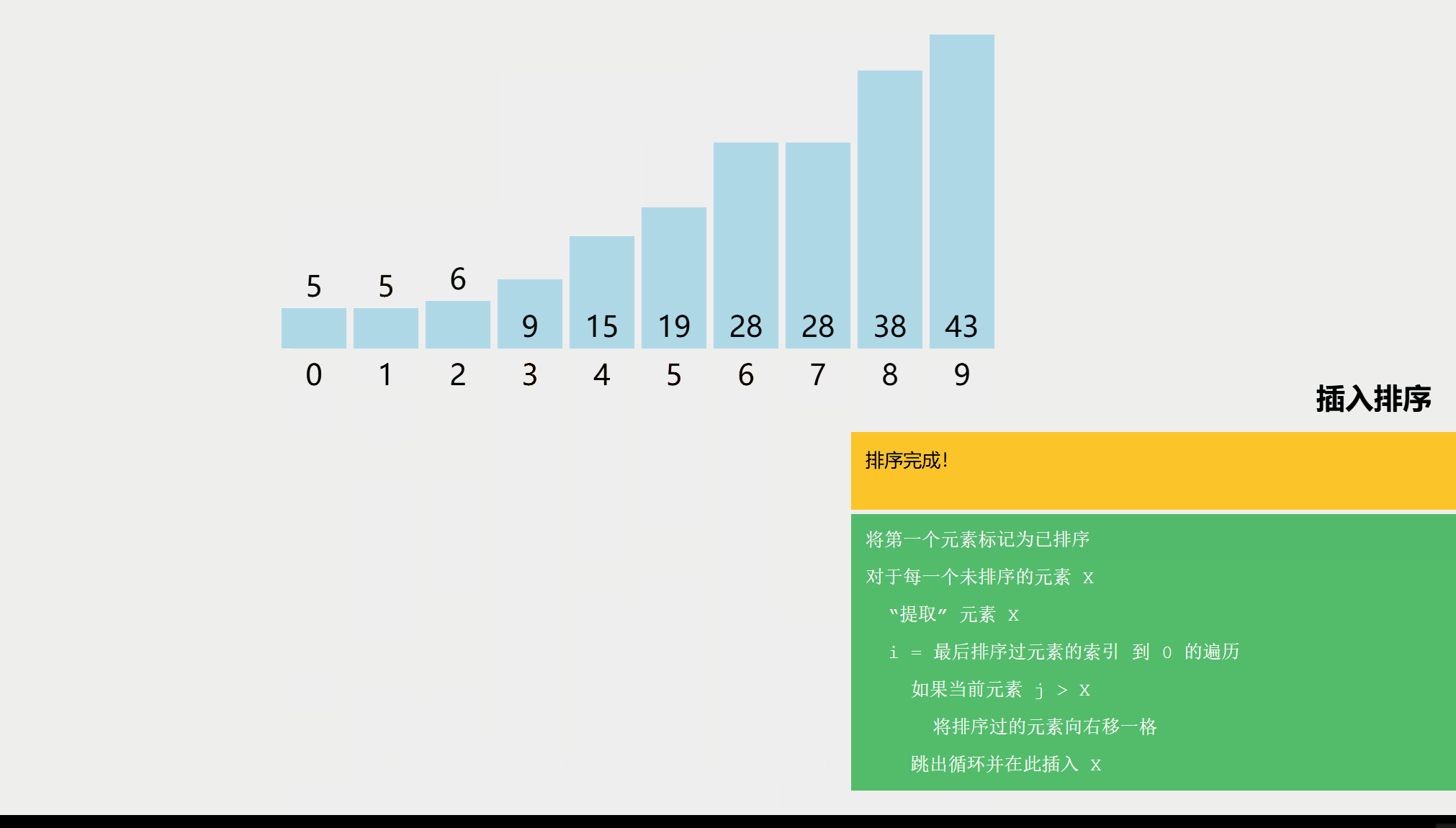
算法思想
每次将一个待排序的记录按其关键字大小插入到前面已排序好的子序列中,直到全部记录插入完成。
-
代码
不带哨兵:
void InsertSort(int A[],int n){ int i,j,temp; for(i=0;i<n;i++){ if(A[i]<A[i-1]){ temp=A[i]; for(j=i-1;j>=0&&A[j]>temp;j--){ //向后挪位 A[j+1]=A[j]; } A[j+1]=temp;//插入 } } }带哨兵(第一个元素存待插入的元素):
优点:不用每轮循环都判断j>=0
void InsertSort(int A[],int n){ int i,j; for(i=2;i<=n;i++){ if(A[i]<A[i-1]){ A[0]=A[i]; //哨兵 for(j=i-1;A[0]<A[j];j--) //从后往前查找待插入位置 A[j+1]=A[j]; A[j+1]=A[0]; } } } -
算法效率
-
空间复杂度: O ( 1 ) O(1) O(1)
-
时间复杂度:主要来自对比关键字、移动元素。
最好情况:共n-1趟处理,每一趟只需要对比一次,则 O ( n ) O(n) O(n)
最坏情况:原本为逆序,则 O ( n 2 ) O(n^2) O(n2)
平均时间复杂度: O ( n 2 ) O(n^2) O(n2)
算法稳定性:稳定
-
1.2 折半插入排序
-
算法思想
在已排好的部分设置low和high指针,取中间点mid和待排序数据比较。
当low>high时折半查找停止,应将[low,i-1]内的元素全部右移,并将A[0]复制到low所指位置;
当A[mid]==A[0]时,为了保证算法的稳定性,应继续在mid所指位置右边寻找插入位置。
-
代码
void InsertSort(int A[],int n){ int i,j,low,high,mid; for(i=2;i<=n;i++){ A[0]=A[i]; low=1;high=i-1; //折半查找范围 while(low<=high){ mid=(low+high)/2; if(A[mid]>A[0]) high=mid-1; //查找左子表 else low=mid+1; //查找右子表 for(j=i-1;j>=high+1;i--) A[j+1]=A[j]; //后移元素,空出插入位置 A[high+1]=A[0]; //插入 } } } -
算法效率
时间复杂度: O ( n 2 ) O(n^2) O(n2)
-
对链表进行插入排序
- 折半插入排序无法实现
- 直接插入排序移动元素次数变少了,但关键字比较次数依然 O ( n 2 ) O(n^2) O(n2),所以时间复杂度也是 O ( n 2 ) O(n^2) O(n2)。
1.3 希尔排序
-
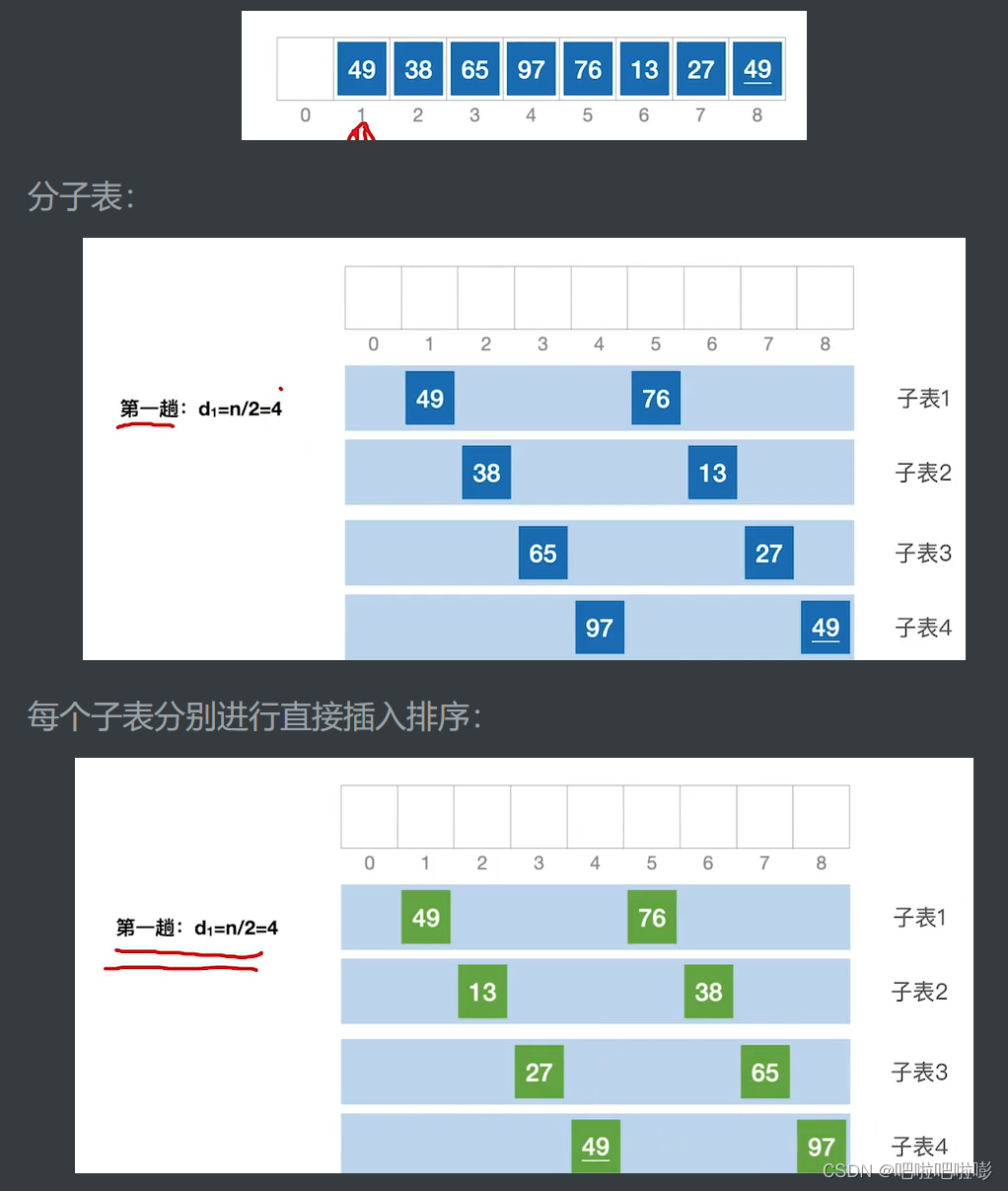
思想
先部分有序,再全局有序。
先将待排序表分割成若干形如 L [ i , i + d , i + 2 d , . . . , i + k d ] L[i,i+d,i+2d,...,i+kd] L[i,i+d,i+2d,...,i+kd]特殊子表,对各个子表分别进行直接插入排序。缩小增量d,重复上述过程,直到d=1为止。
-
过程

-
代码
void ShellSort(int A[],int n){ int d,i,j; //A[0]只是暂存单元,不是哨兵,当j<=0时,插入位置已到 for(d=n/2;d>=1;d=d/2){ //步长变化 for(i=d+1;i<=n;i++){ if(A[i]<A[i-d]){ //需将A[i]插入有序增量子表 A[0]=A[i]; for(j=i-d;j>0&&A[0]<A[j];j-=d){ A[j+d]=A[j]; //记录后移 } A[j+d]=A[0]; //插入 } } } } -
性能分析
-
空间复杂度: O ( 1 ) O(1) O(1)
-
时间复杂度:和增量序列d的选择有关。
目前无法用数学手段确切证明时间复杂度,最坏时间复杂度 O ( n 2 ) O(n^2) O(n2),n在某个范围内,可达 O ( n 1.3 ) O(n^{1.3}) O(n1.3)
-
不稳定
-
不能基于链表实现。
-
2.交换排序
- 基于交换的排序:根据序列中两个元素关键字的比较结果来对这两个记录在序列中的位置。
2.1 冒泡排序
-
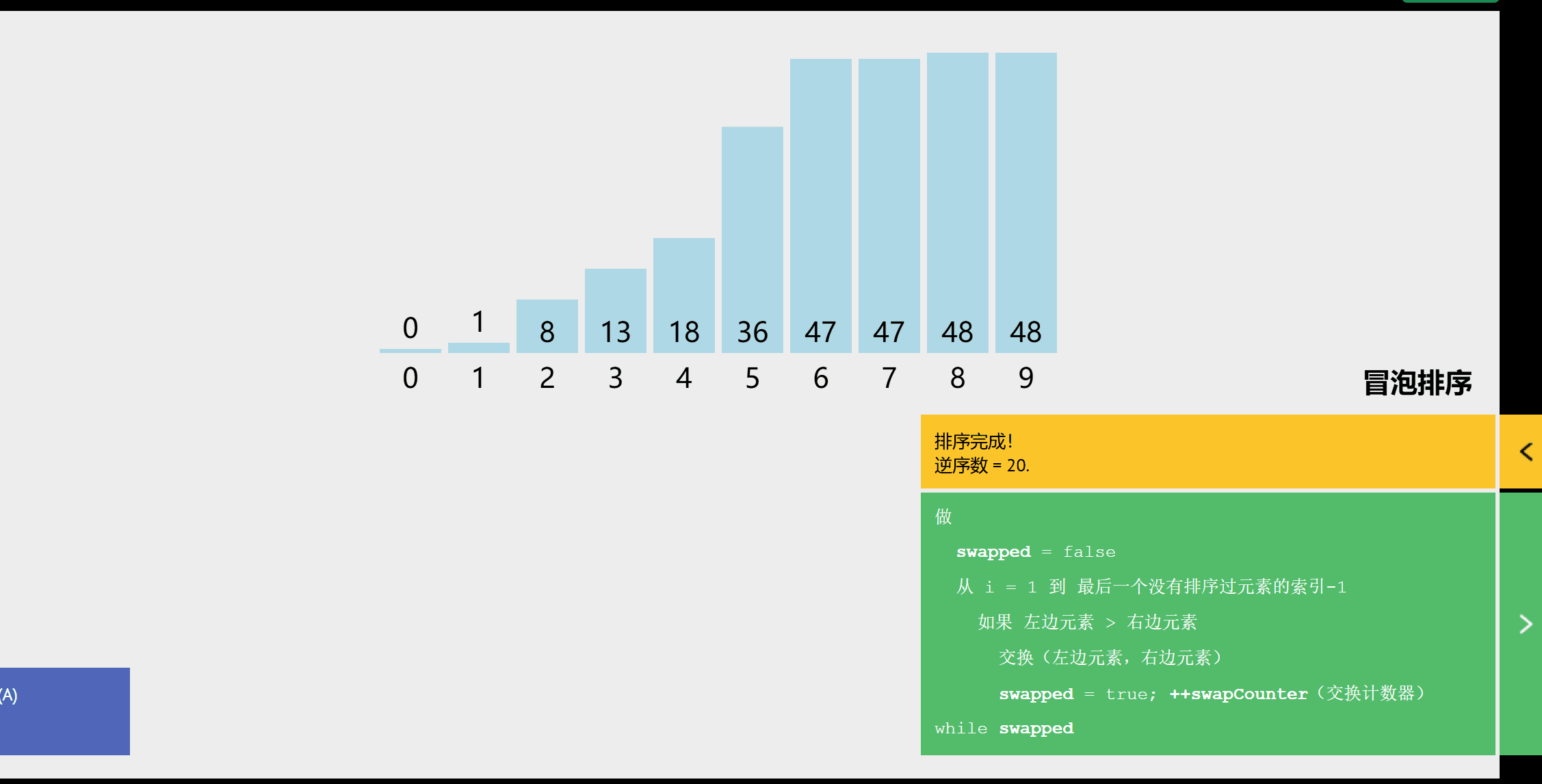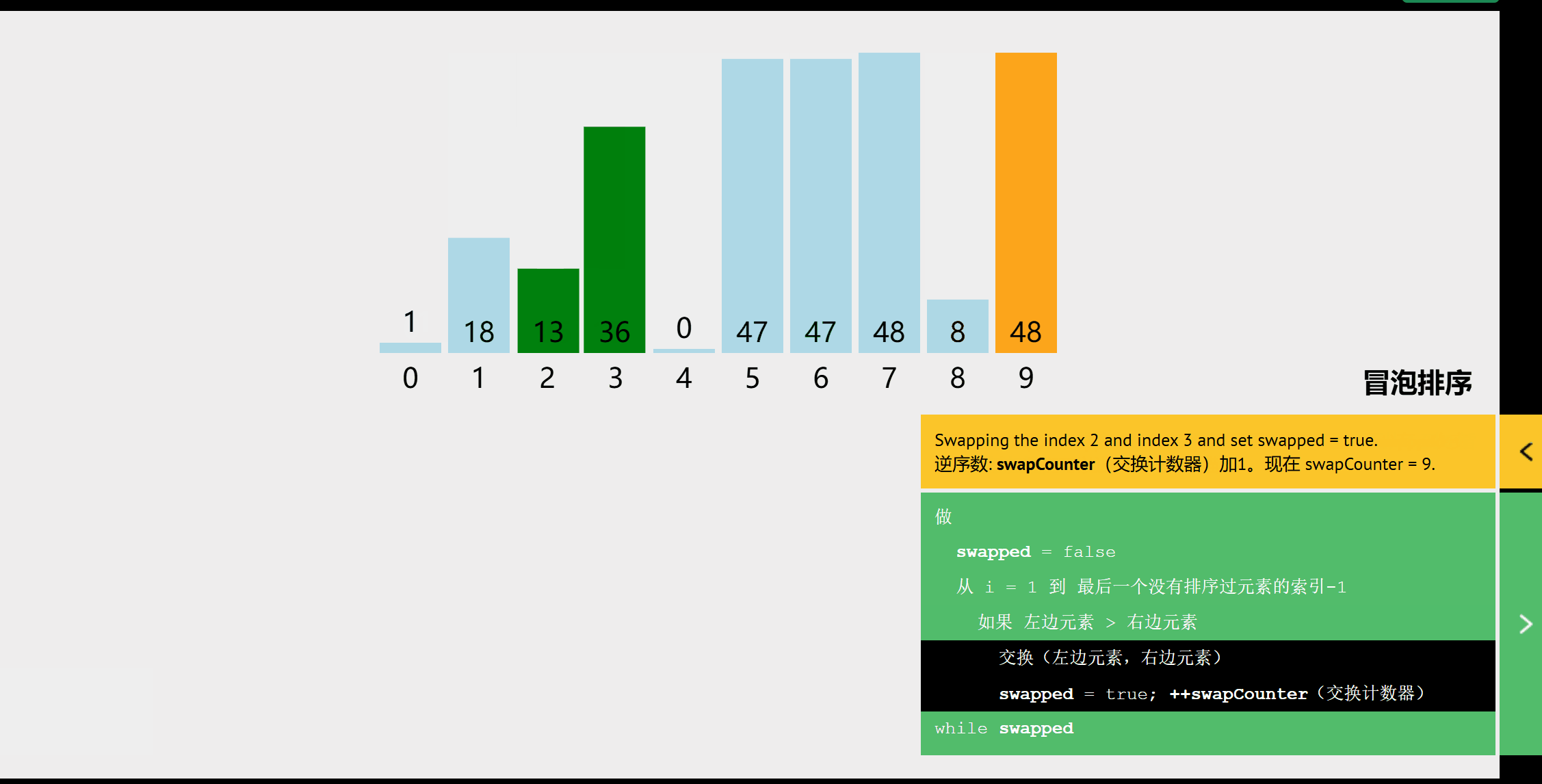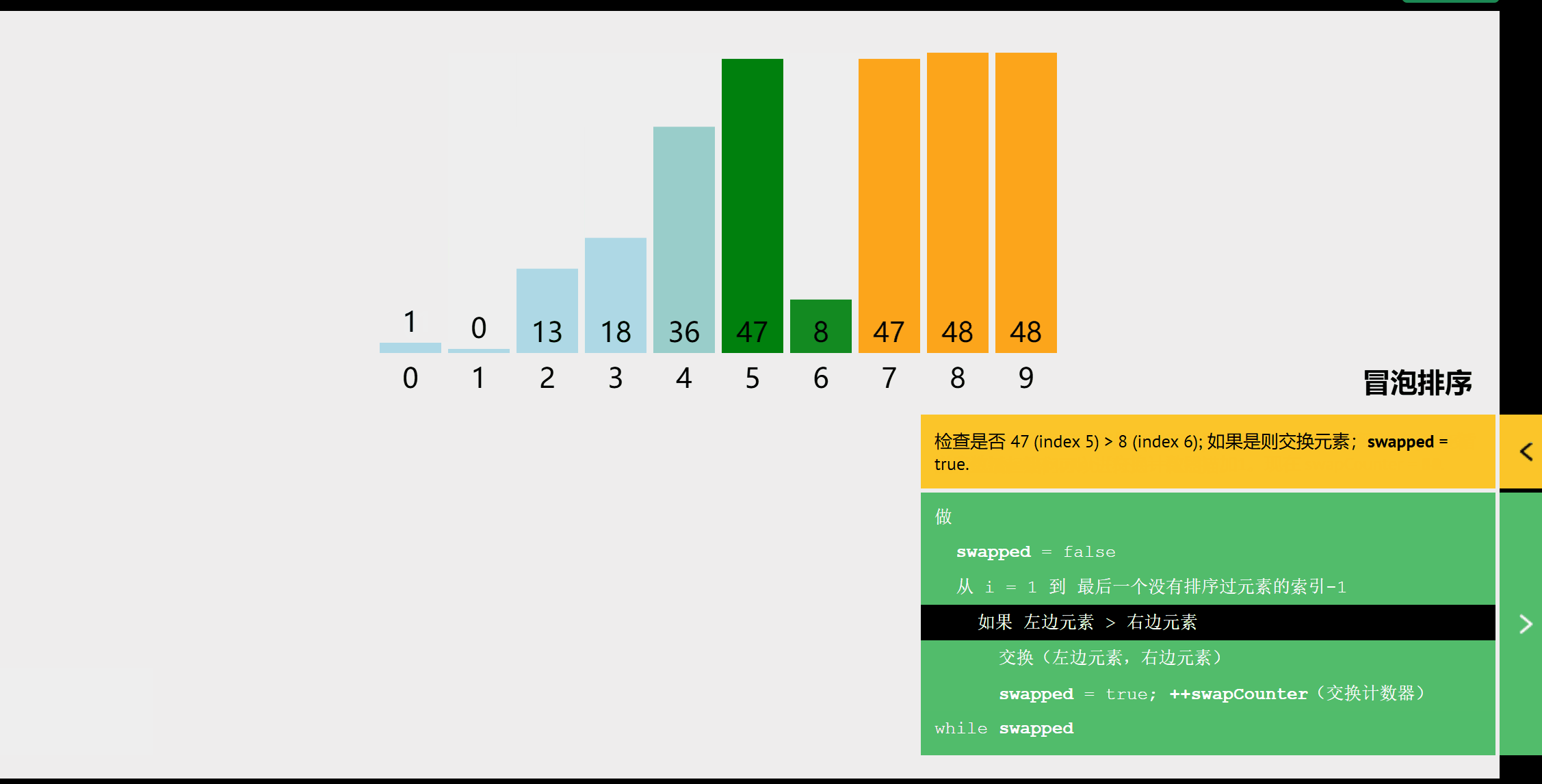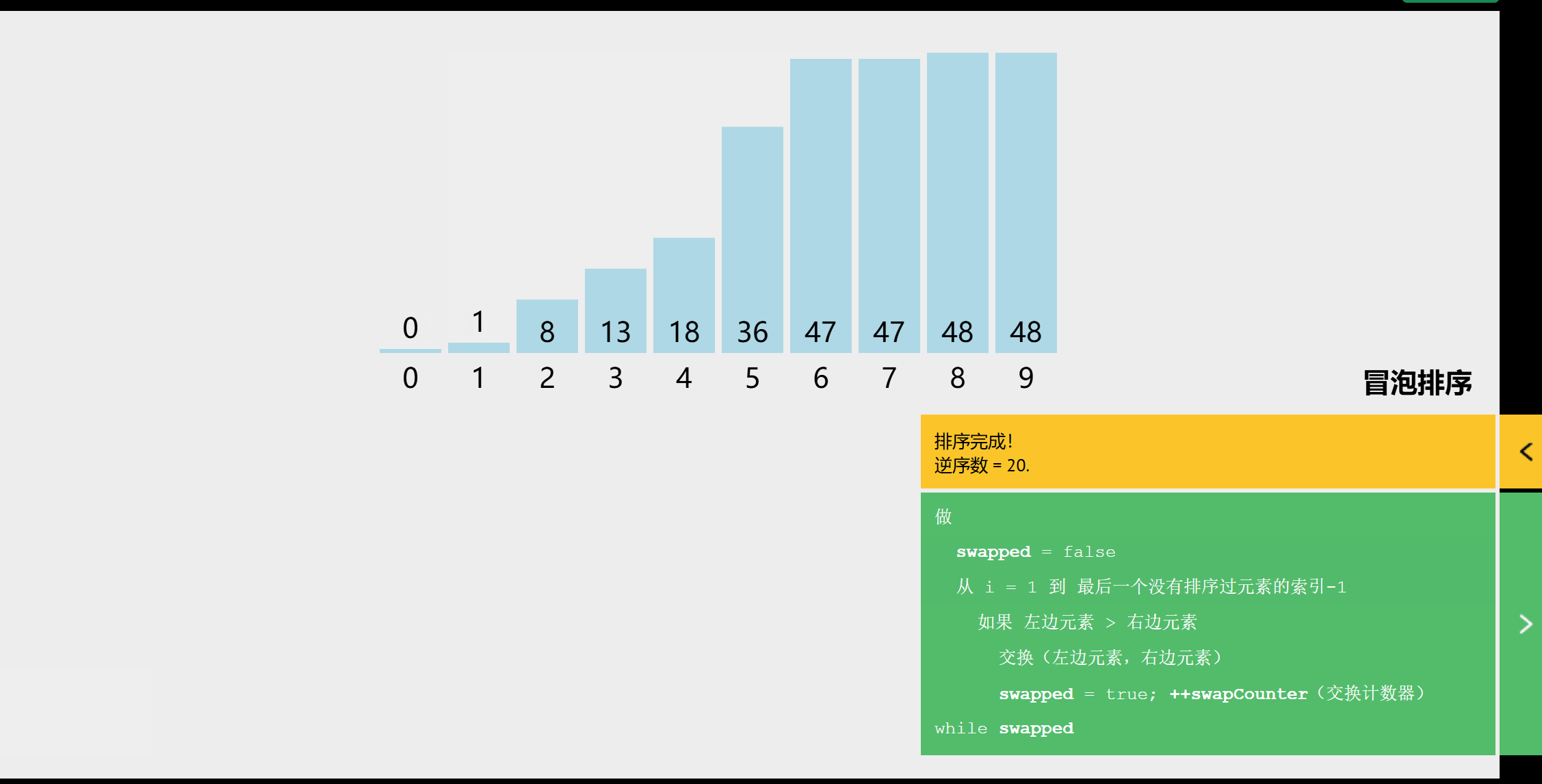
算法思想
从后往前(或从前往后)两两比较相邻元素的值,若为逆序,则交换,直到序列比较完。
-
代码
//交换 void swap(int &a,int &b){ int temp=a; a=b; b=temp; } //冒泡排序 void BubbleSort(int A[],int n){ for(int i=0;i<=n-1;i++){ bool flag=false; //表示本趟是否发生交换 for(int j=n-1;j>i;j--){ if(A[j-1]>A[j]){ //若为逆序 swap[A[j-1],A[j]]; flag=true; } } if(flag==false)return ; //本趟遍历没有发生交换,说明已经有序 } } -
性能分析
-
空间复杂度: O ( 1 ) O(1) O(1)
-
时间复杂度:
最好情况——有序 O ( n ) O(n) O(n)
最坏情况——逆序 O ( n 2 ) O(n^2) O(n2)
-
可以用于链表的排序。
-
2.2 快速排序
-
算法思想
基于分治法。
1.在序列中任取一个元素作为基准(通常取首元素);
2.遍历序列,将比基准元素小的放在基准元素的左边,比基准元素大的放在右边;
3.遍历完成后,基准元素位置确定,对该基准元素的左右子表再次排序。
-
代码
思路
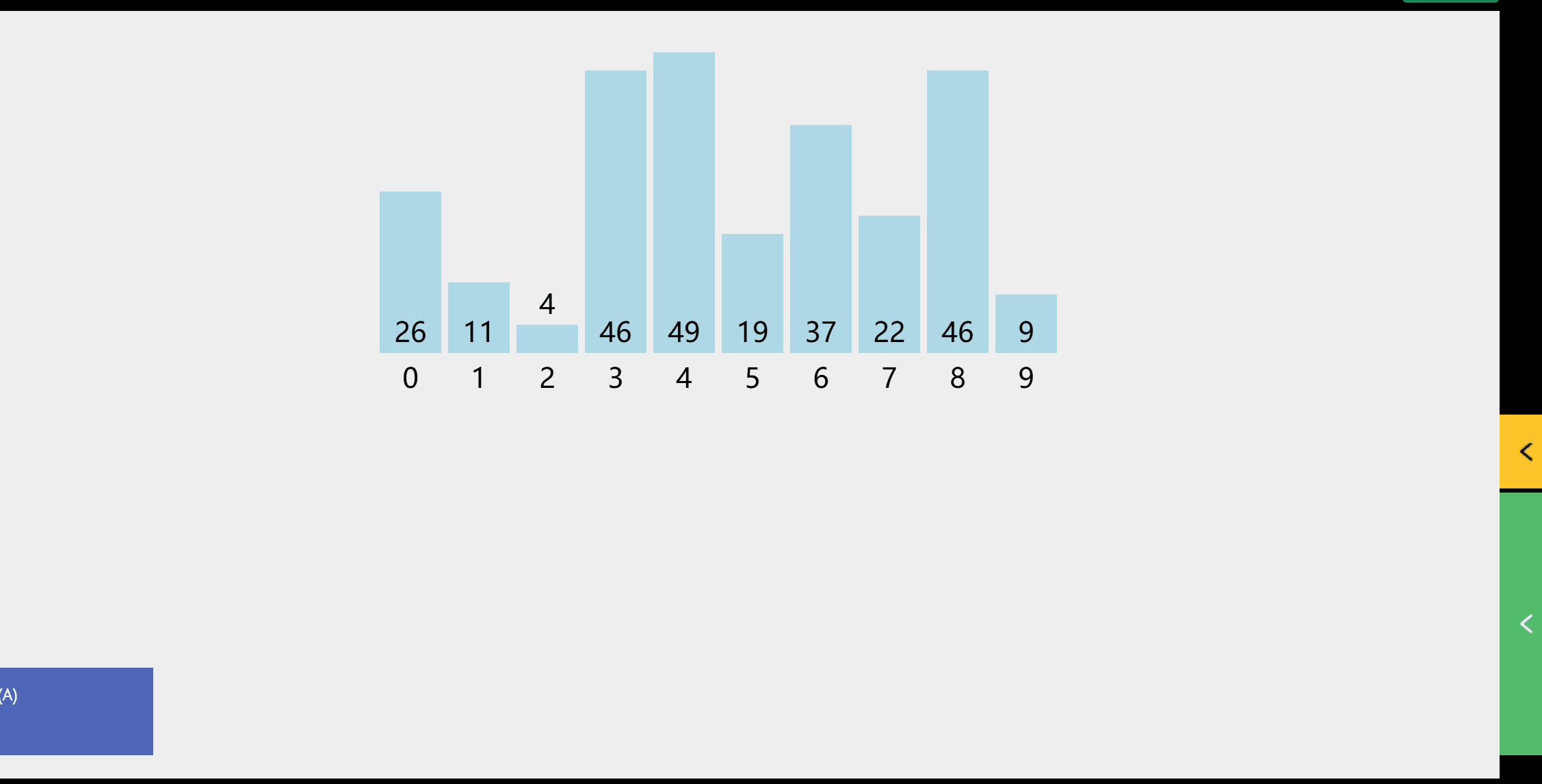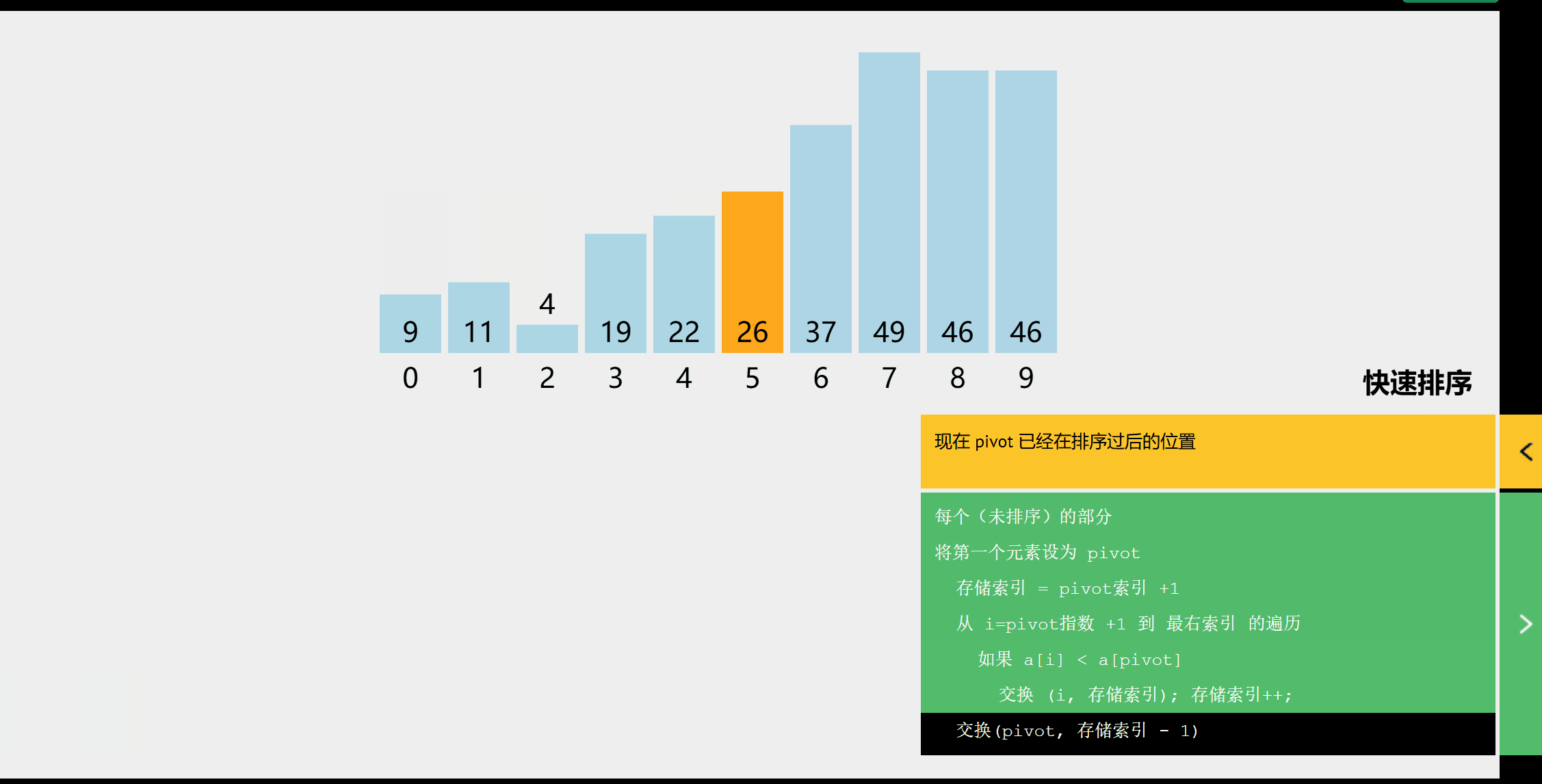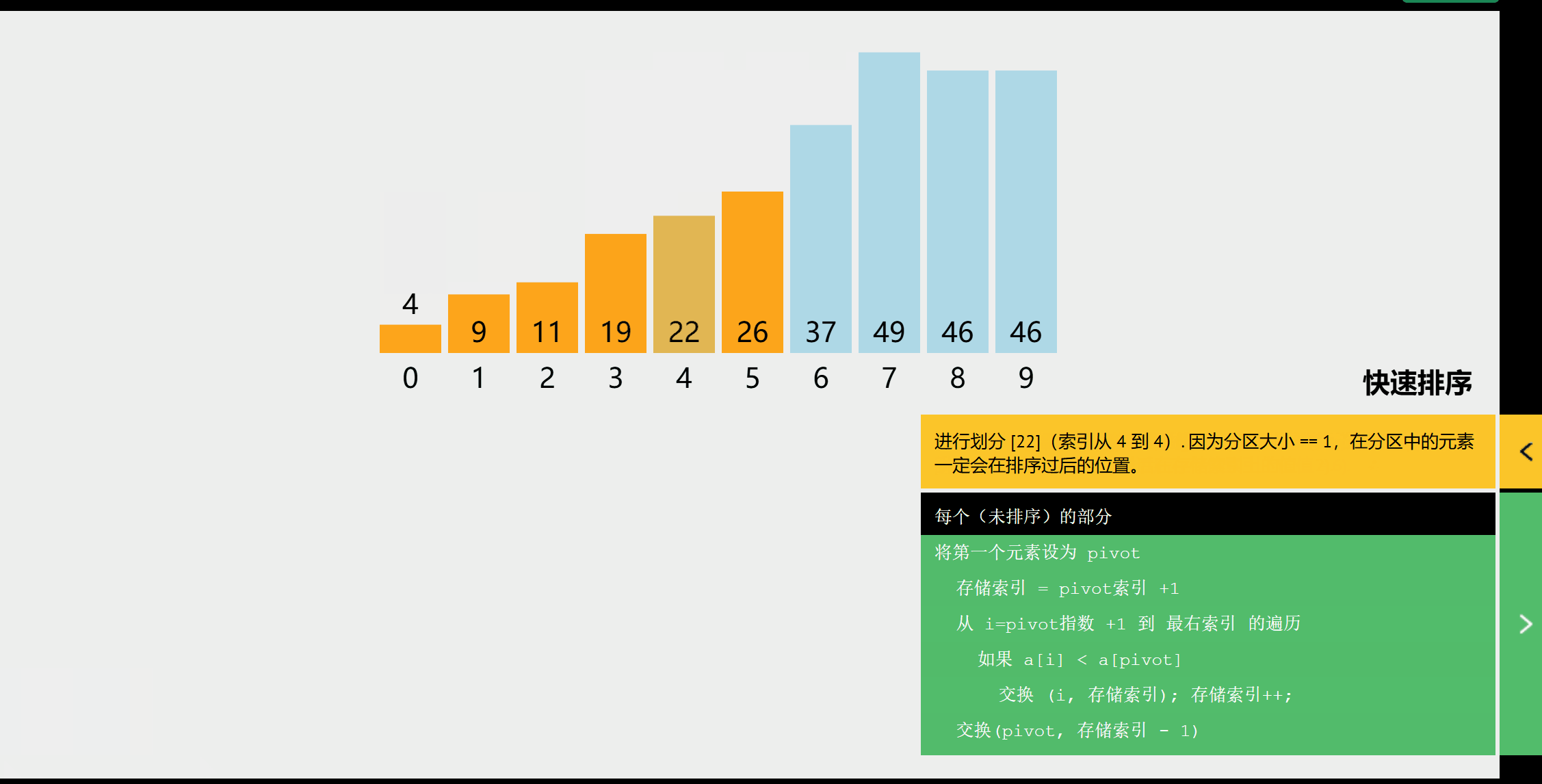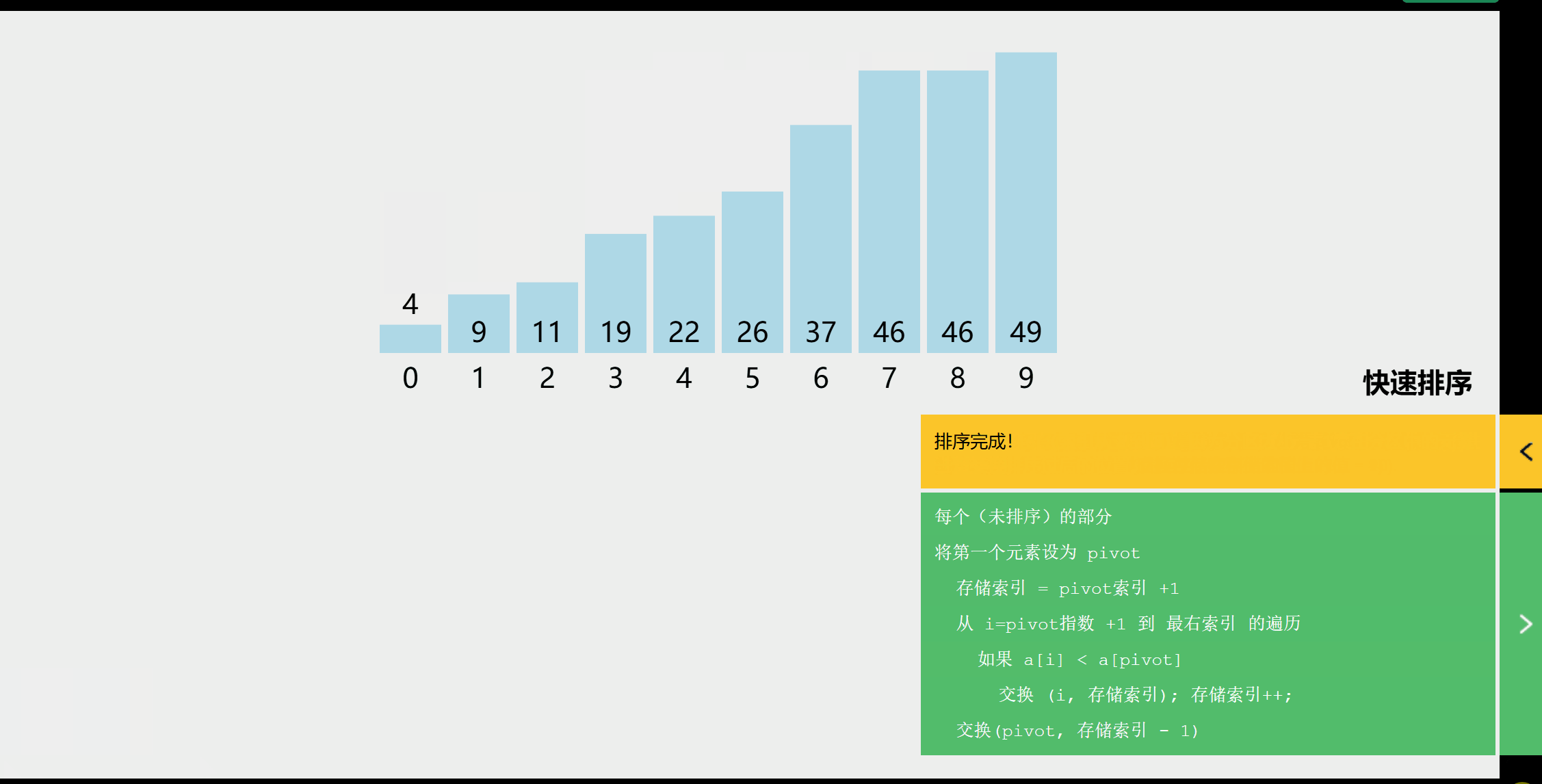
1.以序列第一个元素作为基准元素pivot;
2.令low和high分别指向序列首尾;
3.high不断左移直到找到比pivot小的元素,找到后交换low和high所指元素的位置;
4.low不断右移直到找到比pivot大的元素,找到后交换low和high所指元素位置;
5.当low==high时完成遍历,将基准元素放入low指针所指的地方,此时基准元素已经排序完成;
6.递归排序基准元素的左右子序列。
//用第一个元素将待排序序列划分为左右两个部分 int Partition(int A[],int low,int high){ int pivot=A[low]; //第一个元素作为基准 while(low<high){ while(low<high&&A[high]>=pivot) //high指针不断左移,直到找到比基准元素小的 high--; A[low]=A[high]; //比基准小的元素左移 while(low<high&&A[low]<=pivot) //low指针不断右移,直到找到比基准元素大的 low++; A[high]=A[low]; //比基准元素大的移动到右侧 } A[low]=pivot; //基准元素存放的最终位置 return low; //返回基准元素的位置 } //快速排序 void QuickSort(int A[],int low,int high){ if(low<high){ int pivotpos=Partition(A,low,high); //划分 QuickSort(A,low,pivotpos-1); //划分左子表 QuickSort(A,pivotpos+1,high); //划分右子表 } } -
效率分析
-
空间复杂度=递归层数
每次递归可以用二叉树来表示,则:
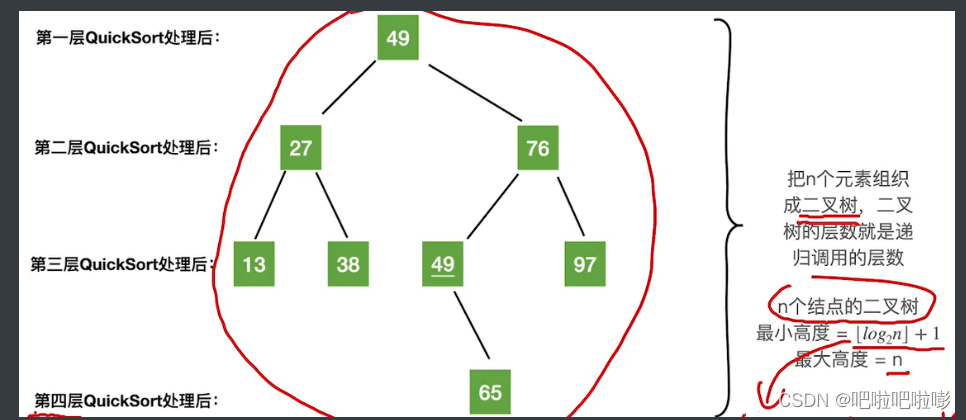
∴最好空间复杂度 O ( l o g 2 n ) O(log_2n) O(log2n),最坏空间复杂度 O ( n ) O(n) O(n)
-
时间复杂度=n*递归层数
最好时间复杂度 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n),最坏时间复杂度 O ( n 2 ) O(n^2) O(n2)
平均时间复杂度 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
-
稳定性:不稳定
-
-
优化
-
若每次选中的基准元素将待排序序列划分成均匀两个部分,则递归深度最小,算法效率最高。
-
优化思路:
尽量选择可以把数据中分的数轴元素。
如:1.选头中尾三个位置的元素,取中间值作为基准元素;2.随机选取一个元素。
-
3.选择排序
3.1 简单选择排序
-
定义
每一趟在待排序元素中选取关键字最小的元素加入有序子序列。
-
代码
//交换函数 void swap(int &a,int &b){ int temp=a; a=b; b=temp; } void SelectSort(int A[],int n){ for(int i=0;i<n-1;i++){ int min=i; for(int j=1+1;j<n;j++) //选择最小的 if(A[j]<A[min])min=j; if(min!=i)swap(A[i],A[min]); } } -
性能分析
-
空间复杂度: O ( 1 ) O(1) O(1)
-
时间复杂度: O ( n 2 ) O(n^2) O(n2)
无论有序、逆序、乱序,一定需要n-1趟处理
总共需要对比关键字 ( n − 1 ) + ( n − 2 ) + . . . + 1 = n ( n − 1 ) / 2 (n-1)+(n-2)+...+1=n(n-1)/2 (n−1)+(n−2)+...+1=n(n−1)/2
交换元素次数<n-1
-
稳定性:不稳定。
-
实用性:既可以顺序表,也可以链表。
-
3.2 堆
3.2.1 堆排序
-
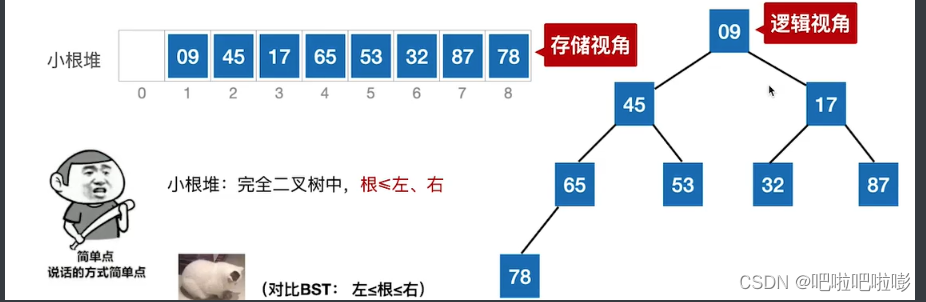
什么是堆?
若n个关键字序列 L [ 1... n ] L[1...n] L[1...n]满足以下某条性质,则称为堆(Heap):
1.若满足 L ( i ) > = L ( 2 i ) L(i)>=L(2i) L(i)>=L(2i)且 L ( i ) > = L ( 2 i + 1 ) L(i)>=L(2i+1) L(i)>=L(2i+1) ( 1 < = i < = n / 2 ) (1<=i<=n/2) (1<=i<=n/2) —— 大根堆(大顶堆)

2.若满足 L ( i ) < = L ( 2 i ) L(i)<=L(2i) L(i)<=L(2i)且 L ( i ) < = L ( 2 i + 1 ) L(i)<=L(2i+1) L(i)<=L(2i+1) ( 1 < = i < = n / 2 ) (1<=i<=n/2) (1<=i<=n/2) —— 小根堆(小顶堆)
-
如何建立大根堆
- 思路:把所有非终端结点( l e n / 2 到 1 len/2到1 len/2到1的结点)都检查一遍,是否满足大根堆要求,如果不满足,则调整。
- 检查方式:检查当前结点是否满足 根>=左右,若不满足,将当前结点与更大的一个孩子互换。
-
代码
思路:
1.从
len/2开始遍历;2.检查是否满足大/小根堆的要求;
3.若不满足,将当前结点与更加大/小的孩子换。
//建立大根堆 void BuildMaxHeap(int A[],int len){ for(int i=len/2;i>0;i--) //从后往前调整所有非终端结点 HeadAdjust(A,i,len); } //将以k为根的子树调整为大根堆 void HeadAdjust(int A[],int k,int len){ A[0]=A[k]; //A[0]暂存子树根结点 for(int i=2*k;i<=len;i*=2){ //沿key较大的子结点向下筛选 if(i<len&&A[i]<A[i+1])//取key较大的子结点的下标 i++; if(A[0]>=A[i]) break; //筛选结束 else{ A[k]=A[i]; //将A[i]调整到双亲结点上 k=i; //修改k值,以便继续向下筛选 } } A[k]=A[0]; //被筛选结点的值放入最终位置 } -
基于大根堆进行排序
1.每一趟将堆顶元素加入有序子序列;
2.与待排序序列中的最后一个元素交换;
3.并将待排序元素序列再次调整为大根堆(小元素不断下坠)。
代码:
//建立大根堆 void BuildMaxHeap(int A[],int len) //将以k为根的子树调整为大根堆 void HeadAdjust(int A[],int k,int len) //堆排序完整逻辑 void HeapSort(int A[],int len){ BuidMaxHeap(A,len); //初始建堆 for(int i=len;i>1;i--){ swap(A[i],A[1]); //堆顶和堆底元素交换 HeadAdjust(A,1,i-1); //把剩余的待排序元素整理成堆 } } -
时间复杂度分析
-
一个结点,每下坠一层,最多只需对比关键字2次
若树高为h,某结点在第i层,则将这个结点向下调整最多只需要下坠h-i层,关键字对比次数不超过2(h-i)
-
建堆过程,关键字对比次数不超过4n,建堆时间复杂度 O ( n ) O(n) O(n)
-
每下坠一层,最多只需要对比关键字两次,因此每一趟排序复杂度不超过 O ( h ) = O ( l o g 2 n ) O(h)=O(log_2n) O(h)=O(log2n)
-
总共有n-1趟,总时间复杂度为 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
-
-
稳定性
若左右孩子一样大,优先和左孩子换,建堆时是稳定的,但是在排序时,堆顶和堆底互换,不稳定。
∴不稳定
-
空间复杂度: O ( 1 ) O(1) O(1)
3.2.2 堆插入删除
-
在堆中插入新元素
-
对于小根堆,新元素放到表尾(堆底),与父节点对比,若新元素比父节点更加小,则互换。
新元素一路上升,直到无法继续上升。
-
对于大根堆,新元素放到表尾,与父节点对比,若新元素比父节点更加大,则互换。
新元素一路上升,直到无法继续上升。
-
-
在堆中删除
-
被删除元素用堆底(表尾)元素代替,
根据大/小根堆要求,让该元素不断下坠,直到无法下坠为止。
-
-
关键字对比次数
每次上升只需对比1次;
每次下降可能2次(有两小孩),可能1次(只有一小孩)。
*完善代码 堆
#include <stdio.h>
#include <math.h>
// 辅助函数,用于交换两个整数的值
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 将以k为根的子树调整为大根堆
void HeadAdjust(int A[], int k, int len) {
A[0] = A[k]; // A[0]暂存子树根结点
for (int i = 2 * k; i <= len; i *= 2) { // 沿key较大的子结点向下筛选
if (i < len && A[i] < A[i + 1]) // 取key较大的子结点的下标
i++;
if (A[0] >= A[i])
break; // 筛选结束
else {
A[k] = A[i]; // 将A[i]调整到双亲结点上
k = i; // 修改k值,以便继续向下筛选
}
}
A[k] = A[0]; // 被筛选结点的值放入最终位置
}
// 建立大根堆
void BuildMaxHeap(int A[], int len) {
// 从最后一个非终端节点开始,依次向前调整堆
for (int i = len / 2; i > 0; i--) {
HeadAdjust(A, i, len);
}
}
// 堆排序完整逻辑
void HeapSort(int A[], int len) {
BuildMaxHeap(A, len); // 初始建堆
for (int i = len; i > 1; i--) {
swap(&A[i], &A[1]); // 堆顶和堆底元素交换
HeadAdjust(A, 1, i - 1); // 把剩余的待排序元素整理成堆
}
}
// 插入新元素到大根堆
void Insert(int A[], int *len, int value) {
A[++(*len)] = value; // 在数组末尾插入新元素
int i = *len;
while (i > 1 && A[i / 2] < A[i]) { // 向上调整
swap(&A[i / 2], &A[i]);
i /= 2;
}
}
// 删除大根堆的根节点
void DeleteMax(int A[], int *len) {
A[1] = A[(*len)--]; // 用最后一个元素替换根节点,并减少堆的大小
HeadAdjust(A, 1, *len); // 调整堆
}
// 打印堆的结构
void PrintHeap(int A[], int len) {
for (int i = 1; i <= len; i++) {
printf("%d ", A[i]);
}
printf("\n");
}
// 打印堆的结构(水平树格式)
void PrintHeapStructure(int A[], int len) {
int levels = (int)log2(len) + 1; // 计算堆的层数
int maxWidth = (1 << (levels - 1)) * 3; // 每层最大宽度
for (int level = 0; level < levels; level++) {
int numElements = 1 << level; // 当前层的元素数量
int spaceBetween = maxWidth / numElements; // 当前层元素之间的间隔
for (int i = 0; i < numElements && (numElements + i - 1) < len; i++) {
int index = numElements + i; // 元素的实际索引
printf("%*s%d", spaceBetween / 2, "", A[index]); // 打印元素
}
printf("\n");
}
}
int main() {
int A[100] = {0, 6, 2, 10, 8, 7, 9, 3, 5, 4, 1}; // 注意索引0不使用
int len = 10;
printf("Original array:\n");
PrintHeap(A, len);
printf("Heap structure:\n");
PrintHeapStructure(A, len);
// 堆排序
HeapSort(A, len);
printf("Sorted array:\n");
PrintHeap(A, len);
printf("Heap structure:\n");
PrintHeapStructure(A, len);
// 插入新元素
Insert(A, &len, 15);
printf("After insert 15:\n");
PrintHeap(A, len);
printf("Heap structure:\n");
PrintHeapStructure(A, len);
// 删除堆顶元素
DeleteMax(A, &len);
printf("After deleting root:\n");
PrintHeap(A, len);
printf("Heap structure:\n");
PrintHeapStructure(A, len);
return 0;
}
4.归并、基数、计数排序
4.1 归并排序
-
定义
-
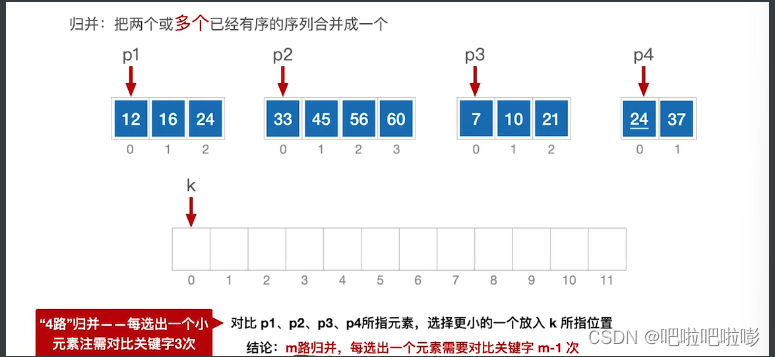
归并:把两个或多个已经有序的序列合并成一个。
-
归并的方法:
1.创建一个长序列,能放下已有的两个序列;
2.i,j分别指向两个有序序列,k指向长序列;
3.对比i,j所指元素,更小的先加入长序列,并且更小的元素所在指针加一;
4.如果i或j已经遍历玩,往长序列中直接添加剩余元素。
-
注:多路归并也一样,m路归并,每选出一个元素要对比m-1次。
-
-
-
归并排序
-
手算模拟:
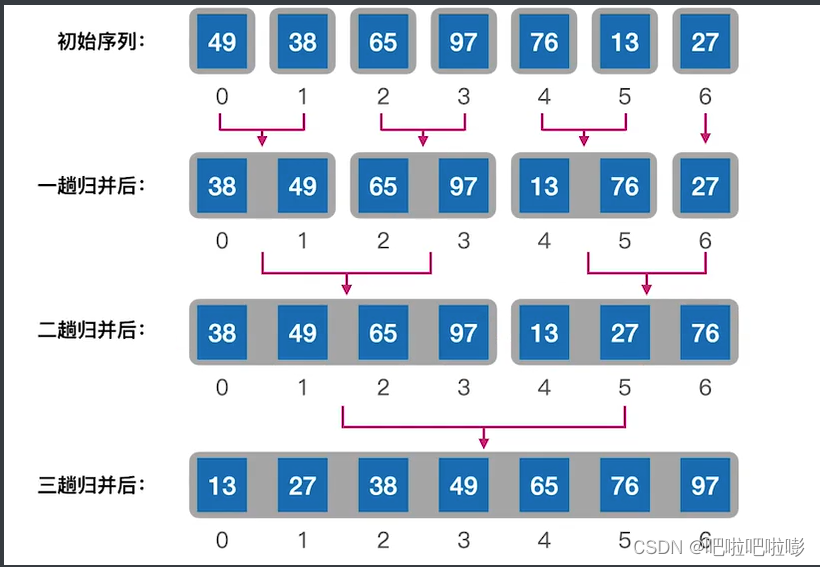
- 核心操作:把两个有序的队列合并成一个
-
-
代码
int *B=(int*)malloc(n*sizeof(int)); //辅助数组 //mid左右两边各自有序,将两部分归并 void Merge(int A[],int low,int mid,int high){ int i,j,k; for(k=low;k<=high;k++){//将A中所有元素复制到B(使最后正确排序还是在A中) B[k]=A[k]; } for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++){ if(B[i]<=B[j]){ //较小值复制到A中 A[k]=B[i++]; } else{ A[k]=B[j++]; } while(i<=mid)A[k++]=B[i++]; while(j<=high)A[k++]=B[j++]; } } void MergeSort(int A[],int low,int high){ if(low<high){ int mid=(low+high)/2; //从中间划分 MergeSort(A,low,mid); //对左半部分归并排序 MergeSort(A,mid,high); //对右半部分递归排序 Merge(A,low,high); //归并 } } -
算法效率分析
-
可把归并过程看成2路归并的归并树——形态上是一棵倒立的二叉树。

-
n个元素进行2路归并排序,归并趟数 = ⌈ l o g 2 n ⌉ =\lceil log_2n \rceil =⌈log2n⌉
每趟归并时间复杂度为 O ( n ) O(n) O(n),则算法时间复杂度为 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
-
空间复杂度= O ( n ) O(n) O(n)
-
稳定性:稳定。
-
4.2 基数排序
-
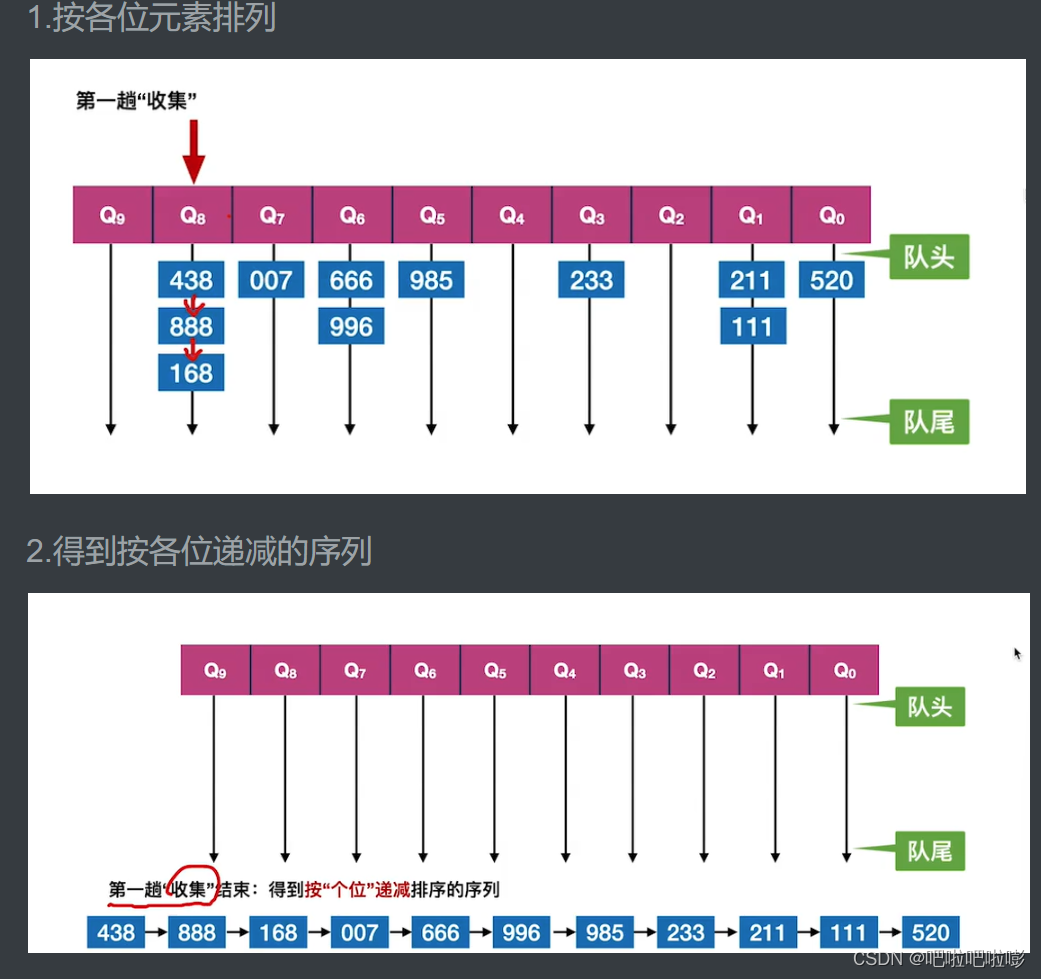
例子
原始序列

1.按各位元素排列


-
定义

-
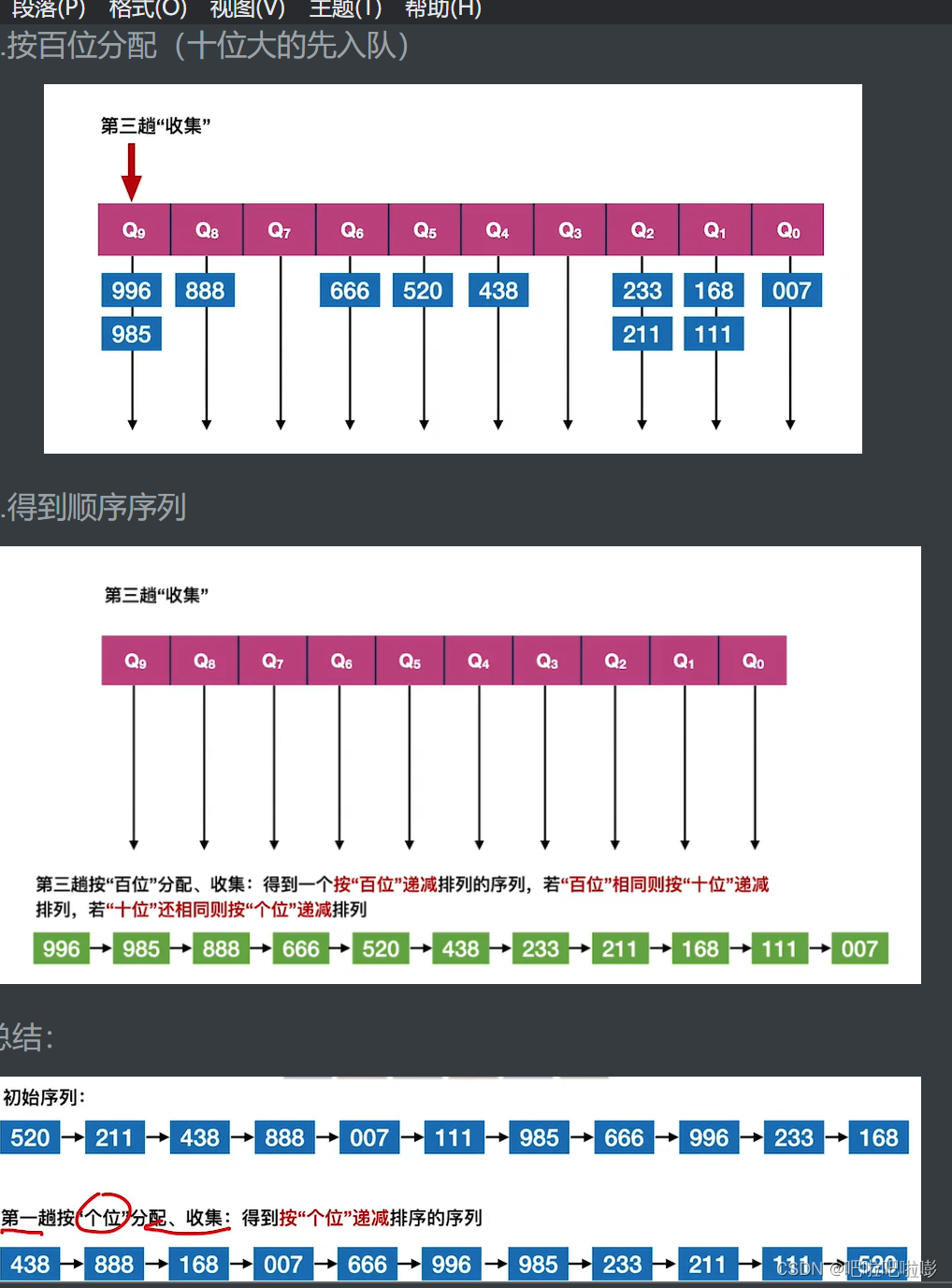
基数排序得到递减序列过程如下:
1.初始化:设置r个空队列
2.按各个关键字位权重递增的次序(个、十、百),对d个关键字位分别做分配和收集。
1)分配:顺序扫描各个元素,若当前处理的关键字位等于x,则将元素插入队尾。
2)收集:把各队列中的结点依次出队并连接。
-
算法效率分析
基数排序通常基于链式存储实现。
- 需要r个辅助队列,空间复杂度 O ( r ) O(r) O(r)
- 一趟分配 O ( n ) O(n) O(n),一趟收集 O ( r ) O(r) O(r),总共d趟分配、收集,总时间复杂度 O ( d ( n + r ) ) O(d(n+r)) O(d(n+r))
-
基数排序完整代码
#include <stdio.h> #include <stdlib.h> // 定义元素类型 typedef int ElemType; // 定义链表节点结构 typedef struct LinkNode { ElemType data; struct LinkNode *next; } LinkNode, *LinkList; // 定义队列结构 typedef struct { LinkNode *front, *rear; } LinkQueue; // 初始化队列 void InitQueue(LinkQueue *q) { q->front = q->rear = (LinkNode *)malloc(sizeof(LinkNode)); if (!q->front) { printf("Memory allocation failed\n"); exit(1); } q->front->next = NULL; } // 判断队列是否为空 int IsEmpty(LinkQueue q) { return q.front == q.rear; } // 入队 void EnQueue(LinkQueue *q, ElemType e) { LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode)); if (!p) { printf("Memory allocation failed\n"); exit(1); } p->data = e; p->next = NULL; q->rear->next = p; q->rear = p; } // 出队 int DeQueue(LinkQueue *q, ElemType *e) { if (IsEmpty(*q)) return 0; LinkNode *p = q->front->next; *e = p->data; q->front->next = p->next; if (q->rear == p) q->rear = q->front; free(p); return 1; } // 获取数组中最大元素的位数 int GetMaxDigits(ElemType arr[], int n) { int max = arr[0]; for (int i = 1; i < n; i++) { if (arr[i] > max) { max = arr[i]; } } int digits = 0; while (max > 0) { digits++; max /= 10; } return digits; } // 获取指定位置的数字 int GetDigit(ElemType num, int pos) { for (int i = 0; i < pos; i++) { num /= 10; } return num % 10; } // 基数排序函数 void RadixSort(ElemType arr[], int n) { int maxDigits = GetMaxDigits(arr, n); // 初始化10个队列用于每个基数位的分配 LinkQueue queues[10]; for (int i = 0; i < 10; i++) { InitQueue(&queues[i]); } // 对每个位数进行分配和收集 for (int d = 0; d < maxDigits; d++) { // 分配阶段:将元素按当前位的值分配到对应的队列 for (int i = 0; i < n; i++) { int digit = GetDigit(arr[i], d); EnQueue(&queues[digit], arr[i]); } // 收集阶段:将各个队列的元素依次出队放回数组 int index = 0; for (int i = 0; i < 10; i++) { ElemType e; while (DeQueue(&queues[i], &e)) { arr[index++] = e; } } // 打印当前步骤的排序结果 printf("After sorting by digit %d: ", d + 1); for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } printf("\n"); } } int main() { ElemType arr[] = {520, 211, 438, 888, 007, 111, 985, 666, 996, 233,168}; int n = sizeof(arr) / sizeof(arr[0]); printf("Original array: "); for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } printf("\n"); RadixSort(arr, n); printf("Sorted array: "); for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } printf("\n"); return 0; }
4.3 计数排序
-
定义
对每个待排序元素x,统计小于x的元素个数,利用信息可以确定x的最终位置。
-
代码
//A[]是输入序列 //B[]是输出序列 //C[]存储计数值 void CountSort(ElemType A[],ElemType B[],int n,int k){ int i,C[k]; for(i=0;i<k;i++){ //初始化计数数组 C[i]=0; } for(i=0;i<n;i++){ //统计每个元素出现次数 C[A[i]]++; } for(i=1;i<k;i++){ C[i]=C[i]+C[i-1]; //C中存小于等于i的个数 } for(i=n-1;i>=0;i--){ B[C[A[i]-1]]=A[i]; //将元素A[i]放在输出数组B的正确位置上 C[A[i]]=C[A[i]]-1; } }
5.内部排序算法的比较
-
内部排序就是在内存中进行的,以上都是内部排序。
-
比较
算法种类 最好时间复杂度 最坏时间复杂度 平均情况 空间复杂度 是否稳定 直接插入排序 O ( n ) O(n) O(n) O ( n 2 ) O(n^2) O(n2) O ( n 2 ) O(n^2) O(n2) O ( 1 ) O(1) O(1) 是 冒泡排序 O ( n ) O(n) O(n) O ( n 2 ) O(n^2) O(n2) O ( n 2 ) O(n^2) O(n2) O ( 1 ) O(1) O(1) 是 简单选择排序 O ( n 2 ) O(n^2) O(n2) O ( n 2 ) O(n^2) O(n2) O ( n 2 ) O(n^2) O(n2) O ( 1 ) O(1) O(1) 否 希尔排序 O ( 1 ) O(1) O(1) 否 快速排序 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) O ( n 2 ) O(n^2) O(n2) O ( l o g 2 n ) O(log_2n) O(log2n) 否 堆排序 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) O ( 1 ) O(1) O(1) 否 二路归并排序 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) O ( n ) O(n) O(n) 是 基数排序 O ( d ( n + r ) ) O(d(n + r)) O(d(n+r)) O ( d ( n + r ) ) O(d(n + r)) O(d(n+r)) O ( d ( n + r ) ) O(d(n + r)) O(d(n+r)) O ( r ) O(r) O(r) 是
*完整代码 排序
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
// 交换
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
//--------------------插入排序--------------------
void InsertSort(int A[], int n) {
int i, j, temp;
for (i = 1; i < n; i++) {
if (A[i] < A[i - 1]) {
temp = A[i];
for (j = i - 1; j >= 0 && A[j] > temp; j--) { // 向后挪位
A[j + 1] = A[j];
}
A[j + 1] = temp; // 插入
}
}
}
//--------------------折半插入排序--------------------
void InsertHaftSort(int A[], int n) {
int i, j, low, high, mid;
for (i = 1; i < n; i++) {
int temp = A[i];
low = 0; high = i - 1; // 折半查找范围
while (low <= high) {
mid = (low + high) / 2;
if (A[mid] > temp)
high = mid - 1; // 查找左子表
else
low = mid + 1; // 查找右子表
}
for (j = i - 1; j >= low; j--)
A[j + 1] = A[j]; // 后移元素,空出插入位置
A[low] = temp; // 插入
}
}
//--------------------希尔排序--------------------
void ShellSort(int A[], int n) {
int d, i, j;
// A[0]只是暂存单元,不是哨兵,当j<=0时,插入位置已到
for (d = n / 2; d >= 1; d /= 2) { // 步长变化
for (i = d; i < n; i++) {
if (A[i] < A[i - d]) { // 需将A[i]插入有序增量子表
int temp = A[i];
for (j = i - d; j >= 0 && temp < A[j]; j -= d) {
A[j + d] = A[j]; // 记录后移
}
A[j + d] = temp; // 插入
}
}
}
}
//--------------------冒泡排序--------------------
void BubbleSort(int A[], int n) {
for (int i = 0; i < n - 1; i++) {
bool flag = false; // 表示本趟是否发生交换
for (int j = n - 1; j > i; j--) {
if (A[j - 1] > A[j]) { // 若为逆序
swap(&A[j - 1], &A[j]);
flag = true;
}
}
if (flag == false) return; // 本趟遍历没有发生交换,说明已经有序
}
}
//--------------------快速排序--------------------
int Partition(int A[], int low, int high) {
int pivot = A[low]; // 第一个元素作为基准
while (low < high) {
while (low < high && A[high] >= pivot) // high指针不断左移,直到找到比基准元素小的
high--;
A[low] = A[high]; // 比基准小的元素左移
while (low < high && A[low] <= pivot) // low指针不断右移,直到找到比基准元素大的
low++;
A[high] = A[low]; // 比基准元素大的移动到右侧
}
A[low] = pivot; // 基准元素存放的最终位置
return low; // 返回基准元素的位置
}
void QuickSort(int A[], int low, int high) {
if (low < high) {
int pivotpos = Partition(A, low, high); // 划分
QuickSort(A, low, pivotpos - 1); // 划分左子表
QuickSort(A, pivotpos + 1, high); // 划分右子表
}
}
//--------------------选择排序--------------------
void SelectSort(int A[], int n) {
for (int i = 0; i < n - 1; i++) {
int min = i;
for (int j = i + 1; j < n; j++) // 选择最小的
if (A[j] < A[min]) min = j;
if (min != i) swap(&A[i], &A[min]);
}
}
//---------------------堆排序--------------------
void HeapAdjust(int A[], int k, int len) {
int temp = A[k]; // A[0]暂存子树根结点
for (int i = 2 * k + 1; i < len; i = 2 * i + 1) { // 沿key较大的子结点向下筛选
if (i + 1 < len && A[i] < A[i + 1]) // 取key较大的子结点的下标
i++;
if (temp >= A[i])
break; // 筛选结束
else {
A[k] = A[i]; // 将A[i]调整到双亲结点上
k = i; // 修改k值,以便继续向下筛选
}
}
A[k] = temp; // 被筛选结点的值放入最终位置
}
// 建立大根堆
void BuildMaxHeap(int A[], int len) {
for (int i = len / 2 - 1; i >= 0; i--) // 从后往前调整所有非终端结点
HeapAdjust(A, i, len);
}
// 堆排序完整逻辑
void HeapSort(int A[], int len) {
BuildMaxHeap(A, len); // 初始建堆
for (int i = len - 1; i > 0; i--) {
swap(&A[i], &A[0]); // 堆顶和堆底元素交换
HeapAdjust(A, 0, i); // 把剩余的待排序元素整理成堆
}
}
//---------------------归并排序--------------------
void Merge(int A[], int B[], int low, int mid, int high) {
int i, j, k;
for (k = low; k <= high; k++) { // 将A中所有元素复制到B
B[k] = A[k];
}
for (i = low, j = mid + 1, k = low; i <= mid && j <= high; k++) {
if (B[i] <= B[j]) { // 较小值复制到A中
A[k] = B[i++];
} else {
A[k] = B[j++];
}
}
while (i <= mid) A[k++] = B[i++];
while (j <= high) A[k++] = B[j++];
}
void MergeSort(int A[], int B[], int low, int high) {
if (low < high) {
int mid = (low + high) / 2; // 从中间划分
MergeSort(A, B, low, mid); // 对左半部分归并排序
MergeSort(A, B, mid + 1, high); // 对右半部分归并排序
Merge(A, B, low, mid, high); // 归并
}
}
int main() {
int A[] = {34, 8, 64, 51, 32, 21};
int n = sizeof(A) / sizeof(A[0]);
printf("Insertion Sort:\n");
InsertSort(A, n);
for (int i = 0; i < n; i++) printf("%d ", A[i]);
printf("\n");
int B[] = {34, 8, 64, 51, 32, 21};
printf("Binary Insertion Sort:\n");
InsertHaftSort(B, n);
for (int i = 0; i < n; i++) printf("%d ", B[i]);
printf("\n");
int C[] = {34, 8, 64, 51, 32, 21};
printf("Shell Sort:\n");
ShellSort(C, n);
for (int i = 0; i < n; i++) printf("%d ", C[i]);
printf("\n");
int D[] = {34, 8, 64, 51, 32, 21};
printf("Bubble Sort:\n");
BubbleSort(D, n);
for (int i = 0; i < n; i++) printf("%d ", D[i]);
printf("\n");
int E[] = {34, 8, 64, 51, 32, 21};
printf("Quick Sort:\n");
QuickSort(E, 0, n - 1);
for (int i = 0; i < n; i++) printf("%d ", E[i]);
printf("\n");
int F[] = {34, 8, 64, 51, 32, 21};
printf("Selection Sort:\n");
SelectSort(F, n);
for (int i = 0; i < n; i++) printf("%d ", F[i]);
printf("\n");
int G[] = {34, 8, 64, 51, 32, 21};
printf("Heap Sort:\n");
HeapSort(G, n);
for (int i = 0; i < n; i++) printf("%d ", G[i]);
printf("\n");
int H[] = {34, 8, 64, 51, 32, 21};
int *tempB = (int *)malloc(n * sizeof(int));
printf("Merge Sort:\n");
MergeSort(H, tempB, 0, n - 1);
for (int i = 0; i < n; i++) printf("%d ", H[i]);
printf("\n");
free(tempB);
return 0;
}


![[随笔] 在CSDN的6周年纪念日随笔](https://img-blog.csdnimg.cn/direct/e9c556e4b70145d19e3e5d29c05b074b.png)









![[Algorihm][简单多状态DP问题][买卖股票的最佳时机含冷冻期][买卖股票的最佳时机含手续费]详细讲解](https://img-blog.csdnimg.cn/direct/05f6e39d6ed2412f9876add4ce3e6342.png)