文章目录
- 1.模糊作业车间
- 1.1 模糊数
- 1.2 三角模糊数操作
- 1.3 模糊甘特图
- 2.FJSP+模糊加工时间+GA
- 2.1 GA算法设置
- 2.2 python代码
- 2.3 测试结果
1.模糊作业车间
1.1 模糊数
论域X上的模糊集合A由隶属度函数u(x)表示,u(x)取值[0,1]。如果A为三角模糊数,A可以表示为(a1,aM,a2)。如果A为四角模糊数,A可以表示为(a1,a2,a4,a5)。各模糊数和隶属度函数如下所示:

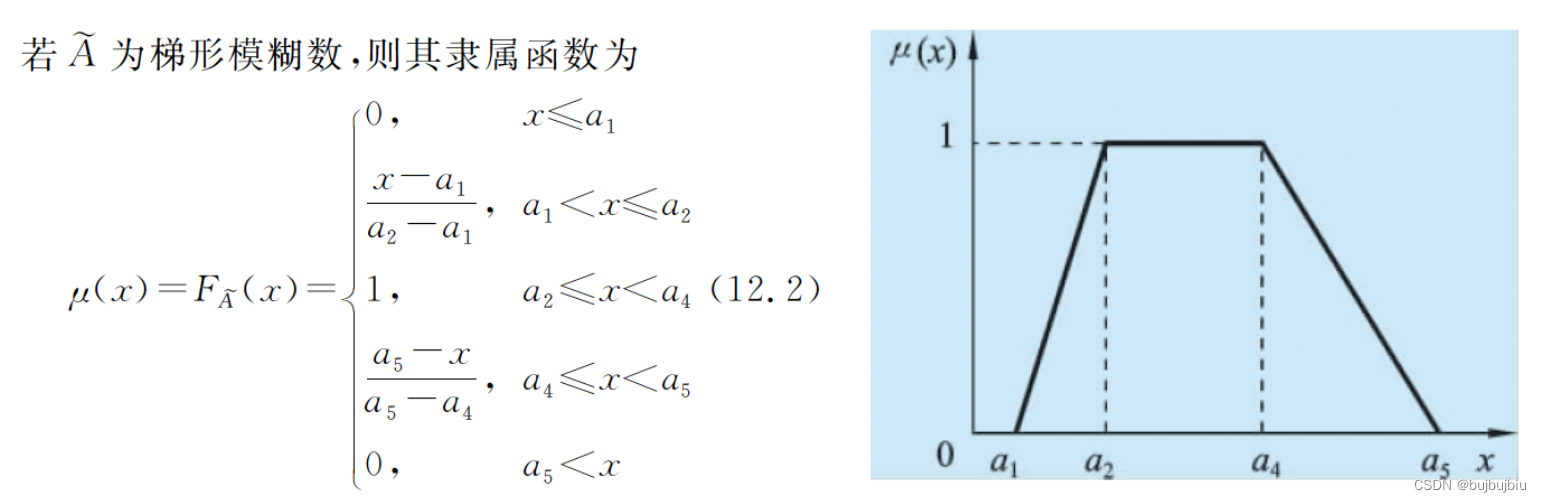
对于不确定条件下的工件加工时间和完工时间,采用三角模糊数来进行描述。对于不确定条件下的交货期,采用梯形模糊数来进行描述。例如job1的第一个操作O11,其在机器1上的模糊加工时间用三角模糊数表示(4,7,12),三个数分别表示最好的,最可能的,最坏的加工时间。一个带有模糊加工时间的4job 和 2machine的柔性作业车间调度问题数据案例如下:括号为实际加工时间,可不考虑

1.2 三角模糊数操作
【1】Sakawa, M., & Mori, T. (1999). An efficient genetic algorithm for job-shop scheduling problems with fuzzy processing time and fuzzy duedate. Computers & Industrial Engineering, 36(2), 325-341. doi:https://doi.org/10.1016/S0360-8352(99)00135-7
【2】Sakawa, M., & Kubota, R. (2000). Fuzzy programming for multiobjective job shop scheduling with fuzzy processing time and fuzzy duedate through genetic algorithms. European Journal of Operational Research, 120(2), 393-407. doi:https://doi.org/10.1016/S0377-2217(99)00094-6
要求解车间调度问题,会遇到加工时间的一些计算,比如求加工开始时间,加工完成时间,和确定数操作一样,模糊数的操作也非常重要,主要包括模糊数的求和和取大操作以及对模糊数的比较。
- 求和:计算每个操作的模糊完成时间[1]
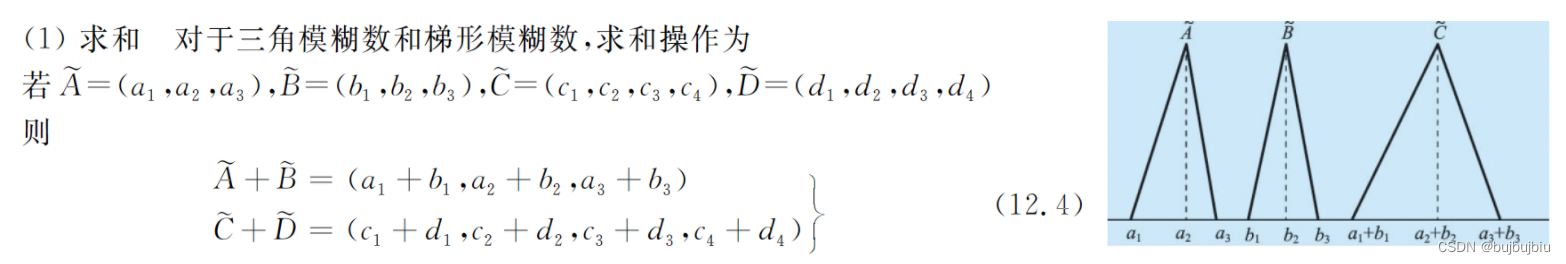
- 取大:计算每个操作的模糊开始时间[1]
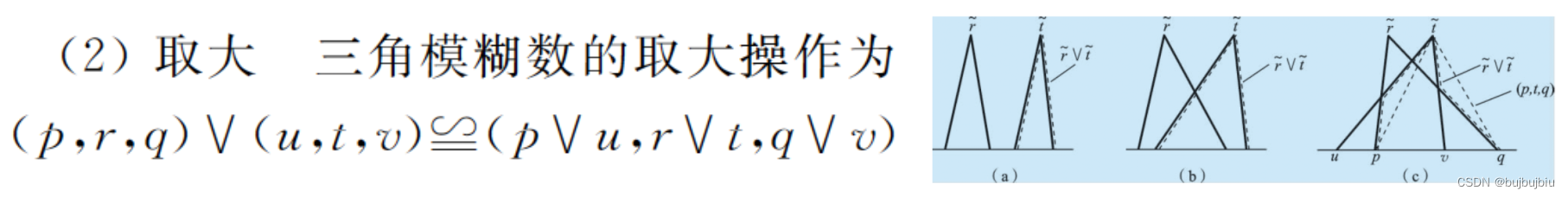
- 比较:模糊完成时间是模糊加工时间的总和,因此也变成了三角模糊数,如果要最小化最大的模糊完成时间,就要比较一些模糊完成时间的值[2]

- 举例
假设有2✖️2的JSP问题:
Job 1: Machine 1 (2, 5, 6), Machine 2 (5, 7, 8)
Job 2: Machine 2 (3, 4, 7), Machine 1 (1, 2, 3)
那么Job1的第二个操作模糊开始时间为(2, 5, 6)V(3, 4, 7),即(3, 5, 7);模糊完成时间为(3, 5, 7)+(5, 7, 8)=(8, 12, 15)
假设有4个三角模糊数为A1=(2,5,8),A2=(3,4,9),A3=(3,5,7),A4=(4,5,8),根据比较原则可得A4,A1,A3,A2
1.3 模糊甘特图
由于每个操作的开始时间和完成时间都是三角模糊数,因此其甘特图也与正常甘特图不同,如下图,每个操作的模糊开始时间在直线下面,模糊完成时间在直线上面,每个三角形就是前面提到的隶属度函数图像。如果是机器上第一个加工,用长方形表示。如O41模糊开始时间为(4,5,7),接下来要在M1上加工,而M1最快的模糊结束时间为O31的(6,10,14),因此O42模糊开始时间为(6,10,14)。


2.FJSP+模糊加工时间+GA
2.1 GA算法设置
复现文章:【3】Lei, D. M. (2010). A genetic algorithm for flexible job shop scheduling with fuzzy processing time. International Journal of Production Research, 48(10), 2995-3013. doi:10.1080/00207540902814348
与前面介绍不同,[3]提出了新的max操作算子,即直接根据rank结果确定,两个三角模糊数s,t中的较大值要么是s,要么是t

- 编码和解码(two-string)
用两层编码表示,一层为操作序列,一层为选择机器,注意第二层的机器分配编码对应的是各个操作按顺序排下来的机器,与第一层编码无关。比如操作011最后加工,加工机器为1。

在部分其它文献中的两层编码,第二层的机器编码对应的是第一层编码下每个操作的加工机器,与此处不同。下面是另一种编码方式,比如操作023最后加工,加工机器为M5。

适应度值为目标函数值(模糊完成时间)
- 选择(tournament select)
使用精英策略,即保留每代种群里最优的个体。由于模糊目标值,轮盘赌选择(roulette wheel)方式不适合,因此使用锦标赛选择(tournament select)。有放回的从种群中随机选择两个个体,选择适应度值较小的个体进入新种群
- 交叉(TPX;GPX/GPPX)
将种群分成两个子种群A和B,分别代表作业序列和机器分配。对于机器分配部分,交叉使用两点交叉(two point crossover TPX)。对于作业序列部分,使用两种交叉:generalised position crossover (GPX)和generalisation of the precedence preservative crossover (GPPX)
GPX:从parent1中选择子字符串S,如S=1231,找到S中每个元素在parent2中的位置并删除对应的元素,注意元素是有顺序的,如S中的1在parent1中是第二次出现,因此要找到parent2中第二次出现的1,删除S后parent2变成32414234,将S插入到parent2中,位置等于S在parent1中的位置,即pos=4

GPPX:设置一个取值[1,2]的string,分表代表从parent1(2)中相继选择基因,如果从parent1中选择了一个基因,删除其在parent2对应的基因

- 变异(swap)
对于某个个体,随机选择两个基因并交换
- 算法
随机生成N个个体的初始种群P;
对P执行tournament select;
将P分成两个子种群A和B,分别代表作业序列和机器分配部分;
对种群A执行GPPX或者GPX交叉和swap变异;
对种群B执行TPX交叉和swap变异;
合并A和B生成新种群并计算适应度值;
迭代直到结束
2.2 python代码
操作序列用GPPX交叉算子,交叉率=0.8,变异率=0.1,种群数=100,迭代数=1000,编码第二种方式,下面是GA部分,完整代码https://github.com/bujibujibiuwang/solve-fuzzy-FJSP-with-GA
import random
from params import get_args
from Shop import Shop
from utils import *
class GA(object):
def __init__(self, args, shop):
self.shop = shop
self.cross_rate = args.cross_rate
self.mutate_rate = args.mutate_rate
self.pop_size = args.pop_size
self.elite_number = args.elite_number
self.chrom_size = self.shop.job_nb * self.shop.op_nb
self.pop = []
def encode(self):
init_pop = []
for _ in range(self.pop_size):
one_string = []
for _ in range(self.shop.op_nb):
one_string += list(np.random.permutation(self.shop.job_nb))
random.shuffle(one_string)
two_string = [random.randint(0, self.shop.machine_nb-1) for _ in range(self.chrom_size)]
individual = np.vstack([one_string, two_string])
init_pop.append(individual)
return np.array(init_pop)
def decode(self, pop1):
fuzzy_fitness = []
certain_fitness = []
for individual in pop1:
fuzzy_completion_time = self.shop.process_decode1(individual)
fuzzy_fitness.append(fuzzy_completion_time)
certain_fitness.append(value(fuzzy_completion_time))
return fuzzy_fitness, certain_fitness
def selection(self, pop2, fuzzy_fitness, certain_fitness):
"""
tournament selection + elite_strategy
"""
pop2 = pop2.tolist()
sorted_pop = sorted(pop2, key=lambda x: certain_fitness[pop2.index(x)], reverse=False)
new_pop = sorted_pop[:self.elite_number]
while len(new_pop) < self.pop_size:
index1, index2 = random.sample(list(range(10, self.pop_size)), 2)
if rank(fuzzy_fitness[index1], fuzzy_fitness[index2]) == fuzzy_fitness[index1]:
new_pop.append(pop[index2])
else:
new_pop.append(pop[index1])
return np.array(new_pop)
def crossover_machine(self, pop_machine):
"""
two point crossover (TPX)
"""
temp = pop_machine.copy().tolist()
new_pop = []
while len(temp) != 0:
parent1, parent2 = random.sample(temp, 2)
temp.remove(parent1)
temp.remove(parent2)
if random.random() < self.cross_rate:
pos1, pos2 = sorted(random.sample(list(range(self.chrom_size)), 2))
offspring1 = parent1[:pos1] + parent2[pos1:pos2] + parent1[pos2:]
offspring2 = parent2[:pos1] + parent1[pos1:pos2] + parent2[pos2:]
else:
offspring1 = parent1
offspring2 = parent2
new_pop.append(offspring1)
new_pop.append(offspring2)
return np.array(new_pop)
def crossover_job(self, pop_job):
"""
generalisation of the precedence preservative crossover (PPX)
"""
temp = pop_job.copy().tolist()
new_pop = []
for parent1 in temp:
if random.random() < self.cross_rate:
new_individual = []
parent2 = pop_job[random.randint(0, self.pop_size-1)].tolist()
string = random.choices([0, 1], k=self.chrom_size)
for choose in string:
if int(choose) == 0:
new_individual.append(parent1[0])
parent2.remove(parent1[0])
parent1 = parent1[1:]
else:
new_individual.append(parent2[0])
parent1.remove(parent2[0])
parent2 = parent2[1:]
new_pop.append(new_individual)
else:
new_pop.append(parent1)
return np.array(new_pop)
def mutation(self, part):
"""
swap
"""
for individual in part:
if random.random() < self.mutate_rate:
pos1, pos2 = random.sample(list(range(self.chrom_size)), 2)
individual[pos1], individual[pos2] = individual[pos2], individual[pos1]
return part
@staticmethod
def elite_strategy(pop3, fitness):
best_fitness = [np.inf, np.inf, np.inf]
best_individual = None
for k, individual in enumerate(pop3):
if rank(fitness[k], best_fitness) == best_fitness:
best_fitness = fitness[k]
best_individual = individual
return best_individual, best_fitness
2.3 测试结果
用文献[3]中instance1测试,文献中instance1求出最优解[20, 31, 40],本人测试最优解[20, 31, 41]
0:old best:[inf, inf, inf], now best:[47, 70, 89], now mean:99.9475
100:old best:[28, 41, 54], now best:[34, 42, 52], now mean:48.41
200:old best:[25, 38, 46], now best:[25, 38, 47], now mean:38.92
300:old best:[25, 36, 45], now best:[25, 36, 45], now mean:38.2425
400:old best:[21, 33, 44], now best:[21, 33, 44], now mean:35.2775
500:old best:[21, 31, 41], now best:[24, 31, 40], now mean:34.475
600:old best:[21, 31, 41], now best:[21, 31, 42], now mean:34.35
700:old best:[19, 31, 42], now best:[19, 31, 42], now mean:33.5275
800:old best:[20, 31, 41], now best:[19, 31, 42], now mean:32.6575
900:old best:[20, 31, 41], now best:[20, 31, 41], now mean:34.175
模糊甘特图如下
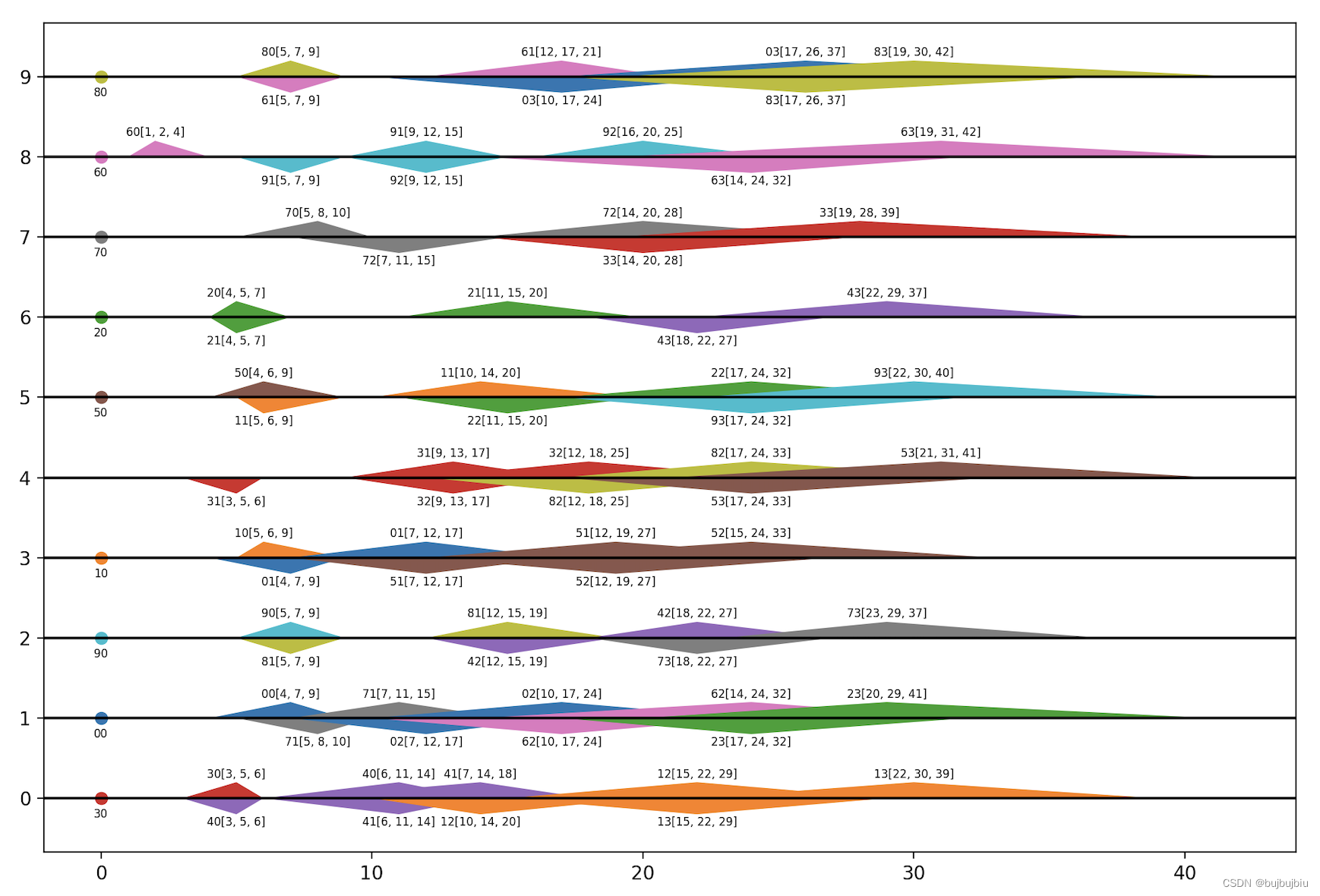
迭代曲线如下